Решением дифференциального уравнения является функция.
Дифференциальные уравнения. Дифференциальное уравнение с разделёнными переменными. Дифференциальные уравнения с разделяющимися переменными.
Определение 1. Уравнение называется дифференциальным, если оно содержит производные искомой функции или её дифференциалы.
Решением дифференциального уравнения является функция.
Решить дифференциальное уравнение, значит найти такую функцию при подстановке которой в уравнение получается верное равенство.
|
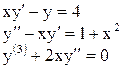 Определение 2. Порядок дифференциального уравнения зависит от порядка входящих в него производных.
Определение 2. Порядок дифференциального уравнения зависит от порядка входящих в него производных.
Определение 3. Общим решением дифференциального уравнения является множество решений, содержащих переменную С.
Определение 4. Частное решение получается из общего путём подстановки вместо С конкретного числа.
Существуют различные виды дифференциальных уравнений. Познакомимся с некоторыми из них.
Дифференциальное уравнение с разделёнными переменными
имеет вид: 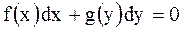
Пример 1. Найдите частное решение дифференциального уравнения 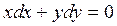 , удовлетворяющего начальным условиям: х = 2; y = - 3.
, удовлетворяющего начальным условиям: х = 2; y = - 3.
Решение:
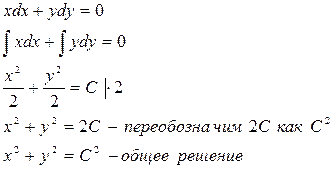

В решении имеем семейство концентрических окружностей с центром в начале координат и радиусом С.
Для нахождения частного решения в общее решение подставим x = 2; y = - 3, получим: 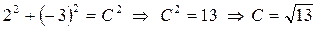
 Подставим значение С в общее решение, получим
Подставим значение С в общее решение, получим
частное решение: 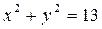 .
.
Пример 2. Найдите частное решение дифференциального уравнения 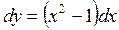 , если y = 4 при х = 1.
, если y = 4 при х = 1.
Решение:
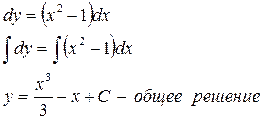

 Для нахождения частного решения в общее решение подставим x = 1; y = 4, получим:
Для нахождения частного решения в общее решение подставим x = 1; y = 4, получим:
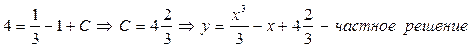
Пример 3. Решите дифференциальное уравнение 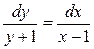 и найдите его частное решение, если при х = 3, y = 3.
и найдите его частное решение, если при х = 3, y = 3.
Решение:
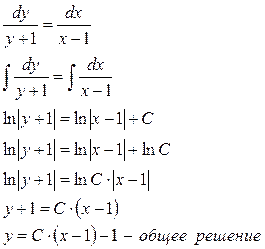

В качестве общего решения мы получили пучок прямых, проходящих через точку
(-1;1) и имеющих угловой коэффициент C.
 Для нахождения частного решения в общее решение подставим x = 3; y = 3, получим:
Для нахождения частного решения в общее решение подставим x = 3; y = 3, получим:
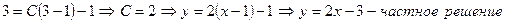
Пример 4. Найдите частное решение дифференциального уравнения 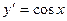 , удовлетворяющее условию
, удовлетворяющее условию 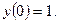
Решение:
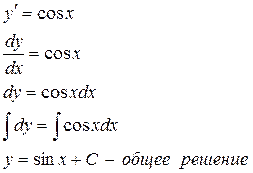

 Для нахождения частного решения в общее решение подставим x = 0; y = 1, получим:
Для нахождения частного решения в общее решение подставим x = 0; y = 1, получим:
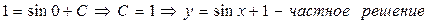
Дифференциальные уравнения с разделяющимися переменными:
Общий вид 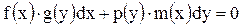
Этапы решения:
- Перейти от производных к дифференциалам: 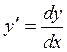 ;
;
- Разделить переменные;
- Проинтегрировать, найти функцию y (общее решение);
- Найти частное решение.
В зависимости от вида уравнения некоторые этапы могут быть упущены.
Пример 1. Найдите частное решение дифференциального уравнения 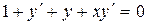 , если y=5 при х=1.
, если y=5 при х=1.
Решение:
1 этап:
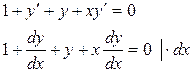
2 этап:
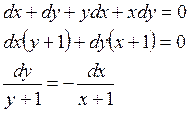
3 этап:

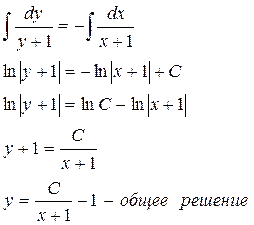
4 этап: найти частное решение, если y=5 при x=1

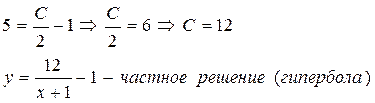
Пример 2. Найдите частное решение дифференциального уравнения 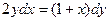 , если y=4 при х=1.
, если y=4 при х=1.
Решение:
2 этап:
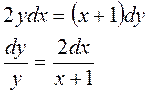
3 этап:

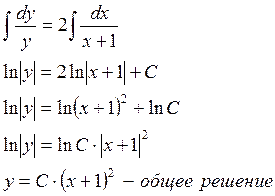
4 этап: найти частное решение, если y=4 при x=1

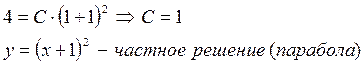
Дата добавления: 2021-02-19; просмотров: 428;











