Основные закономерности течения газа в соплах и диффузорах
В соответствии с уравнением неразрывности потока в стационарном режиме
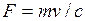 . (7.12)
. (7.12)
Секундный массовый расход т одинаков для всех сечений, поэтому изменение площади сечения F вдоль сопла (по координате х) определяется соотношением интенсивностей возрастания удельного объема газа v и его скорости с. Если скорость увеличивается быстрее, чем удельный объем 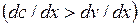 , то сопло должно суживаться, если же
, то сопло должно суживаться, если же 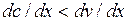 расширяться.
расширяться.
Возьмем дифференциалы от левой и правой частей уравнения (7.11) при условии 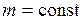 :
:
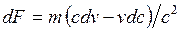 . (7.13)
. (7.13)
Разделив (7.13) на (7.12), получим
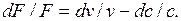 (7.14)
(7.14)
При адиабатном равновесном расширении идеальных газов связь между давлением и объемом описывается уравнением 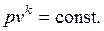
Опыт показывает, что с известным приближением это уравнение применимо и к адиабатному процессу водяного пара (для перегретого пара k=1,3).

 После дифференцирования уравнения адиабаты получаем
После дифференцирования уравнения адиабаты получаем
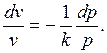
Разделив уравнение 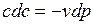 на pv, найдем
на pv, найдем
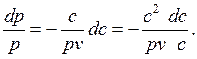 (7.15)
(7.15)
Подставив вместо 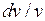 выражение
выражение 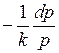 , получим
, получим
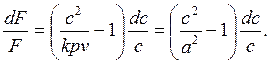 (7.16)
(7.16)
Рассмотрим движение газа через сопло. Поскольку оно предназначено для увеличения скорости потока, то dc>0 и знак у dF определяется отношением скорости потока к скорости звука в данном сечении. Если скорость потока мала (c/a<1), то dF<0 (сопло суживается). Если же c/a>1, то dF>0, т.е. сопло должно расширяться.
На рисунке 7.4 представлены три возможных соотношения между скоростью истечения с2 и скоростью звука а на выходе из сопла. При отношении давлений 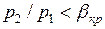 скорость истечения меньше скорости звука в вытекающей среде. Внутри сопла скорость потока также везде меньше скорости звука. Следовательно, сопло должно быть суживающимся на всей длине. Длина сопла влияет лишь на потери от трения, которые здесь не рассматриваются.
скорость истечения меньше скорости звука в вытекающей среде. Внутри сопла скорость потока также везде меньше скорости звука. Следовательно, сопло должно быть суживающимся на всей длине. Длина сопла влияет лишь на потери от трения, которые здесь не рассматриваются.
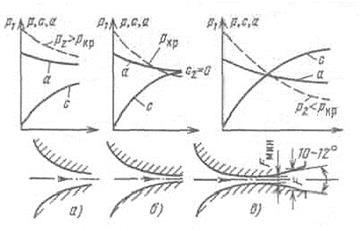
Рисунок 7.4 - Зависимость формы сопла от скорости истечения  :
:
a- 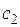 <a; б -
<a; б - 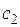 =a в -
=a в - 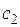 >a
>a
При более низком давлении за соплом можно получить режим, изображенный на рисунке б. В этом случае скорость на выходе из сопла равна скорости звука в вытекающей среде. Внутри сопло по-прежнему должно суживаться (dF<0), и только в выходном сечении dF=0.
Чтобы получить за соплом сверхзвуковую скорость, нужно иметь за ним давление меньше критического (рисунок в). В этом случае сопло необходимо составить из двух частей — суживающейся, где с<а, и расширяющейся, где с>а. Такое комбинированное сопло впервые было применено шведским инженером К. Г. Лавалем в 80-х годах прошлого столетия для получения сверхзвуковых скоростей пара. Сейчас сопла Лаваля применяют в реактивных двигателях самолетов и ракет. Угол расширения не должен превышать 10—12°, чтобы не было отрыва потока от стен.
При истечении газа из такого сопла в среду с давлением меньше критического в самом узком сечении сопла устанавливаются критические давление и скорость. В расширяющейся насадке происходит дальнейшее увеличение скорости и соответственно падение давления истекающего газа до давления внешней среды.
Рассмотрим теперь движение газа через диффузор — канал, в котором давление повышается за счет уменьшения скоростного напора (dc<0). Из уравнения * следует, что если c/a<1, то dF>0, т. е. если скорость газа при входе в канал меньше скорости звука, то диффузор должен расширяться по направлению движения газа так же, как при течении несжимаемой жидкости. Если же скорость газа на входе в канал больше скорости звука (c/a>1), то диффузор должен суживаться (dF<0).
Расчет процесса истечения с помощью h,s-диаграммы
Истечение без трения.Так как водяной пар не является идеальным газом, расчет его истечения лучше выполнять не по аналитическим формулам, а с помощью h, s-диаграммы.
Пусть пар с начальными параметрами вытекает в среду с давлением р2. Если потери энергии на трение при движении водяного пара по каналу и теплоотдача к стенкам сопла пренебрежимо малы, то процесс истечения протекает при постоянной энтропии и изображается на h,s-диаграмме вертикальной прямой 1-2.
Скорость истечения рассчитывается по формуле:
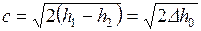 ,
,
где h1 определяется на пересечении линий p1 и t1, а h2 находится на пересечении вертикали, проведенной из точки 1, с изобарой р2 (точка 2).
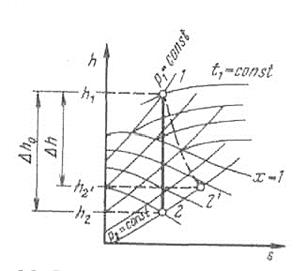
Рисунок 7.5 - Процессы равновесного и неравновесного расширения пара в сопле
Если значения энтальпий подставлять в эту формулу в кДж/кг, то скорость истечения (м/с) примет вид
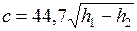 .
.
Действительный процесс истечения. В реальных условиях вследствие трения потока о стенки канала процесс истечения оказывается неравновесным, т. е. при течении газа выделяется теплота трения и поэтому энтропия рабочего тела возрастает.
На рисунке неравновесный процесс адиабатного расширения пара изображен условно штриховой линией 1-2’. При том же перепаде давлений 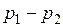 срабатываемая разность энтальпий
срабатываемая разность энтальпий 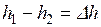 получается меньше, чем
получается меньше, чем 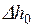 , в результате чего уменьшается и скорость истечения
, в результате чего уменьшается и скорость истечения 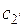 . Физически это означает, что часть кинетической энергии потока из-за трения переходит в теплоту, а скоростной напор
. Физически это означает, что часть кинетической энергии потока из-за трения переходит в теплоту, а скоростной напор 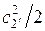 на выходе из сопла получается меньше, чем при отсутствии трения. Потеря в сопловом аппарате кинетической энергии вследствие трения выражается разностью
на выходе из сопла получается меньше, чем при отсутствии трения. Потеря в сопловом аппарате кинетической энергии вследствие трения выражается разностью 
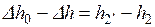 . Отношение потерь в сопле к располагаемому теплопадению называется коэффициентом потери энергии в сопле
. Отношение потерь в сопле к располагаемому теплопадению называется коэффициентом потери энергии в сопле 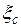 :
:
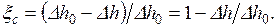
Формула для подсчета действительной скорости адиабатного неравновесного истечения:
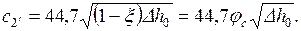
Коэффициент 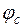 называется скоростным коэффициентом сопла. Современная техника позволяет создавать хорошо спрофилированные и обработанные сопла, у которых
называется скоростным коэффициентом сопла. Современная техника позволяет создавать хорошо спрофилированные и обработанные сопла, у которых 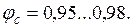
Дата добавления: 2016-11-04; просмотров: 3099;











