Дисперсия оптического вращения в холестерических кристаллах.

Для холестерической фазы характерно спиральное упорядочение с шагом спирали Р. Наличие винтовой оси симметрии обуславливает высокую оптическую активность холестерика. Оптическая активность заключается в повороте плоскости поляризации, проходящего через образец света на угол φ. Вращательная способность вещества определяются как ρ=φ/d, где d – толщина образца. Например, в сахаре ρ~ 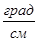, а в холестерике ρ~10⁴ 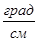. Изучение оптического вращения (0В) обычно проводится в плоскостной текстуре холестерика с оптической осью, перпендикулярной стёклам ячейки. В зависимости от соотношения между шагом спирали Р и длиной волны света λ имеют место три случая.

Если λ<<P , то возможен волноводный режим, когда световое колебание “поворачивается ” в кристалле в соответствии с поворотом молекул в холестерической спирали. Число оборотов плоскости поляризации равно тогда числу шагов Р на толщине образца d.

Если λ<Р , то существует оптическая активность, пропорциональная шагу спирали. Вне района селективного отражения света вращательная способность равна

Здесь Δn=n_е-n₀ – двулучепреломление молекулярного слоя, λ_сел=nP – длина волны селективного отражения света.

Когда λ<<λ_сел , формула преобразуется к простому виду:

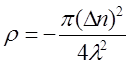
Последняя формула доступна экспериментальной проверке, особенно для холестерических смесей с большим шагом. Примером такой смеси является смесь нематик (90%) – холестерик (10%). Дисперсия ρ и Δn (т.е. их зависимость от λ) может быть чрезвычайно большой.

Третий случай λ≈Р. Тогда наблюдается брегговское отражение света λ_сел=nP; оптическое вращение испытывает аномальную дисперсию в области селективного отражения.

Целью работы является изучение дисперсии оптического вращения (0В) для смеси МББА – холестерил нонаноат. Концентрация холестерика мала (от 5% до 10%), поэтому выполнимо условие λ<P, а величину Δn внутри холестерического слоя можно заменить Δn нематического компонента. Толщина образца d=100мкм.

Для определения дисперсии будем использовать метод канавчатого спектра. Пусть образец помещён между скрещенными поляроидами. Белый свет от осветителя проходит через образец и падает на щель монохроматора УМ-2. спектр, наблюдаемый с помощью спектральной насадки, имеет полосы погасания в тех случаях, где для данной длины волны образец погашен в скрещенных поляроидах. Образец будет погашен только тогда, когда плоскость поляризации света повернётся при прохождении образца на угол, кратный π. Т.е. при переходе от одной длины волны погасания к другой угол меняется на величину π.

Вид канавчатого спектра.

Для канавчатого спектра можно построить график φ(λ). Неопределённость в величине φ равна φ₀. с точность до φ₀ можно определить угол поворота плоскости поляризации при данной длине волны λ_i.

рмула доступна экспериментальной проверке, особенно для холестерических смесей с большим шагом.а на угол

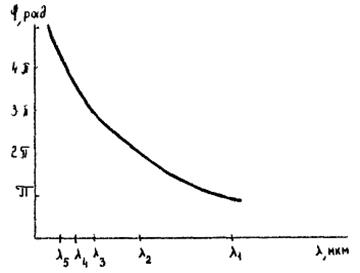
Зависимость φ(λ) по результатам экспериментов. Полученные результаты можно определить в виде φ(1/λ²).

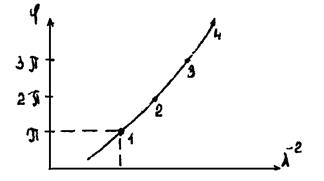
В соответствии с теорией де ВРИ должна наблюдаться прямолинейная зависимость φ~1/λ². искажение формы экспериментальной кривой объясняется дисперсией показателя преломления Δn(λ).

Для МББА тем же методом канавчатого спектра получена зависимость Δn(λ).

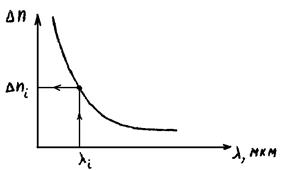
Дисперсия Δn для МББА.

Поэтому более точная зависимость φ~(Δn)² /λ.Используя экспериментальные данные, следует построить график

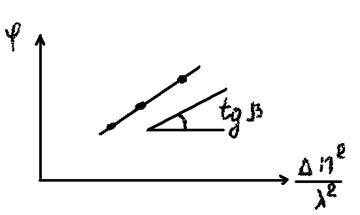
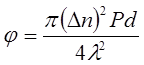
По тангенсу угла наклона определяется шаг спирали холестерика Р.

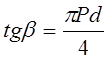
Выполнение работы:

1. Получить канавчатый спектр поглощения холестерической смеси. По градуировочному графику монохроматора определить длины волн поглощения.

2. Построить зависимость φ(λ),φ(1/λ²).

3. По графику Δn(λ) определить Δn для ранее отмеченных длин волн поглощения.

4. Построить зависимость φ(Δn²/ λ²).

5. по тангенсу угла наклона прямой определить шаг холестерической

спирали Р.

Вопросы:

1. нарисуйте плоскостную холестерическую структуру, укажите ось симметрии, а направление с n_II и n_┴ внутри слоя.

2. Что такое оптическая активность?

3. Опишите различные случаи оптической активности холестериков.

4. Объясните “дисперсионный” метод определения шага спирали.