Неуправляемого беспилотного летательного аппарата

В начале эскизного проектирования летательного аппарата (л.а.) проводятся проектировочные расчеты, цель которых состоит в определении значений основных проектных параметров по заданным тактико-техническим требованиям. В дальнейшем на основе значений этих параметров осуществляется эскизное проектирование л.а. В зависимости от вида заданных требований на стадии проектировочных расчетов могут решаться разнообразные задачи. Далее рассматривается одна из таких задач выбора основных проектных параметров применительно к неуправляемому беспилотному л.а.

Поскольку к точности проектировочных расчетов не предъявляется жестких требований, то в качестве математического описания движения л.а. можно использовать уравнения движения л.а. как материальной точки, учитывая лишь основные силы, действующие в полете:

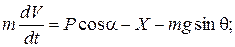(7.11)

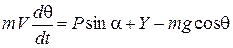. (7.12)

Здесь m – масса л.а., P – тяга двигателя ; X – сила лобового сопротивления, Y – подъемная сила, 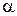– угол атаки, V – скорость центра масс л.а., 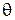– угол наклона скорости V к горизонту.

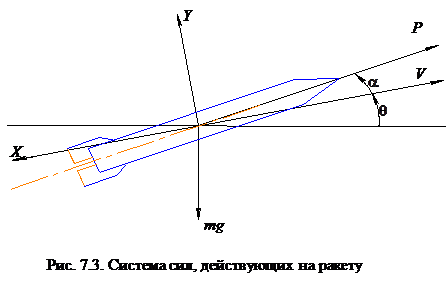Уравнения (7.11), (7.12) получается в результате проектирования всех сил на направление скорости и перпендикуляр к этому направлению, рис. 7.3.

Допустим, что угол атаки 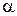мал настолько, что допустимо считать 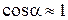, 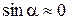. В таком случае, пренебрегая в уравнении (7.12) слагаемым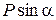и и 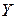, вместо (7.11), (7.12) запишем:

;

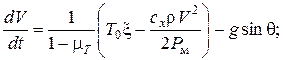
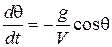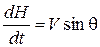; (7.13)

;

,

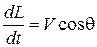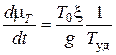где 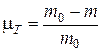– относительная масса израсходованного топлива;

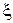– коэффициент, учитывающий изменение тяги двигателя 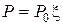, где 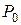– тяга при ;

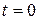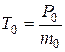– начальная тяговооруженность;

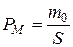– начальная нагрузка на мидель;

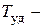удельный импульс, причем .

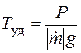Последнее из уравнений системы (7.13) получилось в результате дифференцирования по времени соотношения

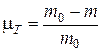
(кстати сказать, это соотношение используется и при записи первого уравнения системы (7.13)).

Эта операция дает зависимость

,

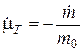которая заменяется тождественной ей записью

,

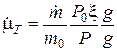что и дает рассматриваемое уравнение, если учесть выражения для начальной тяговооруженности 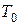и удельного импульса .

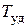Начальное состояние задано:

, , ,

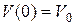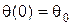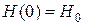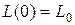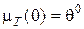, . (7.14)

Характер движения л.а. будет зависеть от параметров, входящих в правую часть уравнений (7.13): 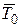, , 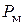, 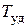от законов изменения величин 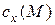, , 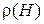а также от продолжительности работы двигателя 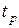(здесь 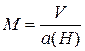– число Маха, 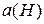– зависимость скорости звука от Н).

Поставим следующую задачу выбора основных проектных параметров л.а.: определить такие 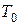, , 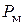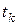( 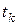– время работы двигателя) из области допустимых значений , , 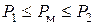, 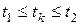чтобы к заданному моменту времени 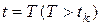для л.а., стартовавшего с начальными условиями (7.14), выполнялись следующие требования по высоте и дальности полета:

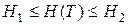; (7.15)

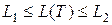, (7.16)

а кроме того, в момент времени 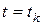выполнялось ограничение на относительную массу израсходованного топлива

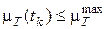. (7.17)

Это задача ОЗП.

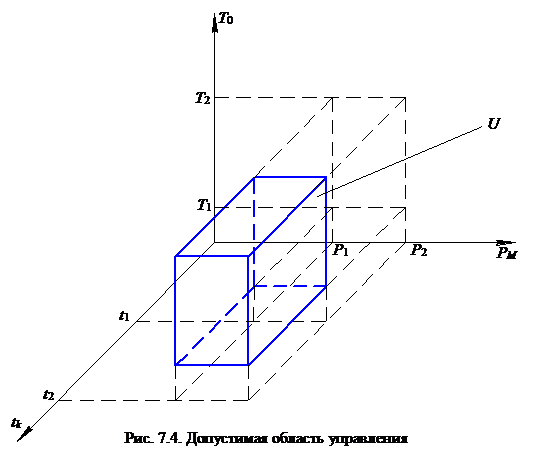В этой задаче управлениями являются постоянные параметры , , 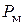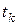. Ограничения (7.15) – (7.17) образуют область управления 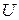, рис. 7.4.

Введем переменные :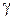

, ;

, ;

, ;

, ;

, .

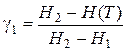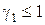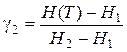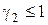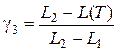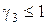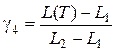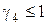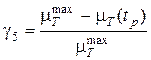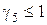ОЗП имеет решение, если согласно теореме разрешимости ОЗП

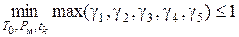. (7.18)

Для нахождения 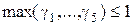необходимо при фиксированных значениях аргументов 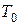, , 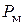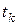проинтегрировать систему уравнений (7.13) при условиях (7.14), определить затем при 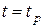значение 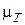, а при 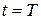значения H и L, вычислить 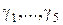и найти наибольший из них. Затем варьируя 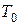, , 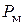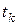нужно стремиться уменьшить это наибольшее значение до выполнения условия (7.18). Так может быть найдено одно из возможных решений задачи ОЗП.