Численные методы решения ОЗП

Решение ОЗП заключается в определении входящих в систему уравнений

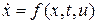
и принадлежащих допустимой области U таких значений управляющих параметров 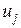, чтобы выполнялись условия , .

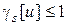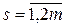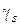
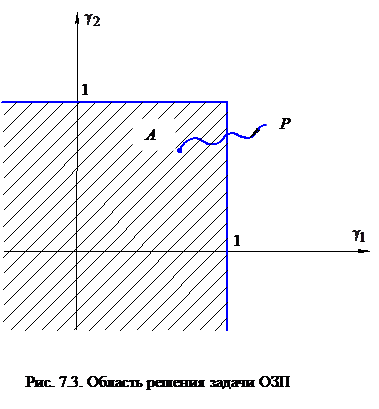
Эти ограничения в 2m-мерном пространстве переменных 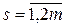выделяют область A. При m = 1 область A имеет вид, представленный на рис.7.2.

Если управление u задано, то в пространстве 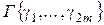получим определенную точку P. ОЗП будет решена, если мы найдем все управления 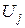, для которых точка P будет находиться в области А. Если точка P находится вне А, то нужно уметь загнать ее в область A. Для этого можно воспользоваться численными методами.

Желаемый результат получается путем последовательного улучшения некоторой меры, характеризующей удаление точки P от области А. Здесь рассмотрим две меры.

Первая из них мера

,

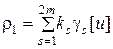где

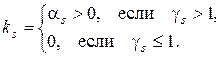
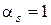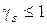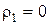В простейшем случае все . Если все , то , т.е. абсолютный минимум меры 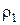равен нулю и он достигается тогда, когда изображающая точка попадает в область А. Если 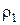не обращается в нуль, то ОЗП не имеет решения. Мера 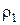не позволяет, однако, оценить степень удаленности точки P от границы области А.

Мера

,

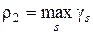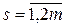
свободная от этого недостатка. Если решение задачи существует, то минимизируя 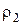можно войти в область A.

Градиентный метод

Задаемся вектором 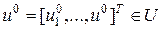, решаем систему 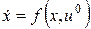, находим 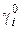, , 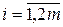определяем , .

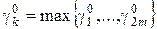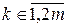Пусть 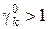. Найдем такую поправку 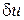к 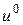, чтобы 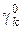уменьшилось. Для этого введем вектор

.

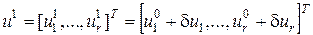Зададим поправки так, что

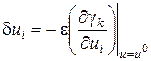
и покажем, что в выражении .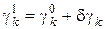

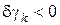Действительно, поскольку

,

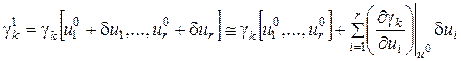то отсюда находим, что

.

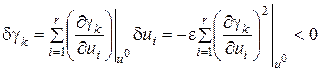Утверждение доказано.