Основная задача проектирования
Постановка задачи. Рассмотрим управляемый процесс, описываемый системой обыкновенных дифференциальных уравнений
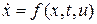 ,
, 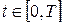 , (7.1)
, (7.1)
где t – время и T – продолжительность процесса; 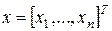 – вектор состояния (вектор фазовых координат);
– вектор состояния (вектор фазовых координат); 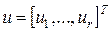 –
– 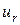 -мерный вектор управления и его компоненты
-мерный вектор управления и его компоненты 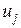 представляют собой кусочно-непрерывные функции времени с конечным числом точек разрыва или постоянные параметры. Значения вектора u принадлежат заданной выпуклой области U r-мерного евклидова пространства
представляют собой кусочно-непрерывные функции времени с конечным числом точек разрыва или постоянные параметры. Значения вектора u принадлежат заданной выпуклой области U r-мерного евклидова пространства 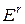 , т.е.
, т.е. 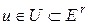 и область U может быть функцией времени. Такие управления будем называть допустимыми. Составляющие
и область U может быть функцией времени. Такие управления будем называть допустимыми. Составляющие 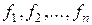 вектора f предполагаются непрерывными и непрерывно дифференцируемыми по всей совокупности своих аргументов.
вектора f предполагаются непрерывными и непрерывно дифференцируемыми по всей совокупности своих аргументов.
Исходное состояние управляемого процесса задано начальными условиями
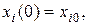
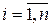 . (7.2)
. (7.2)
Начальные условия (7.2) и управление 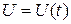 в соответствии с системой (7.1) задают определенную фазовую траекторию процесса
в соответствии с системой (7.1) задают определенную фазовую траекторию процесса 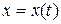 .
.
Пусть на множестве допустимых управлений U(t) и траекторий 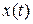 определены функционалы
определены функционалы
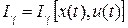 ,
, 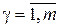 , (7.3)
, (7.3)
каждый из которых имеет смысл конкретного технико-экономического показателя, соответствующего той или иной характеристике управляемой динамической системы. Такими показателями могут быть максимальная перегрузка, перерегулирование, фазовые координаты в некоторые моменты времени (например, значение фазовой координаты 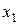 в конечный момент времени, т.е.
в конечный момент времени, т.е. 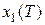 ) или интегральный показатель
) или интегральный показатель
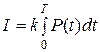 ,
,
где 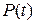 – тяга двигателя, k – коэффициент пропорциональности. Интеграл I характеризует расход топлива.
– тяга двигателя, k – коэффициент пропорциональности. Интеграл I характеризует расход топлива.
Удовлетворительная работа динамической системы полностью характеризуется совокупностью функционалов 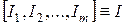 , так что все требования, предъявляемые к системе, сводятся к требованиям на возможные значения этих функционалов. Обычно тактико-технические требования заключаются в указании области изменения критериев в виде неравенств.
, так что все требования, предъявляемые к системе, сводятся к требованиям на возможные значения этих функционалов. Обычно тактико-технические требования заключаются в указании области изменения критериев в виде неравенств.
Таким образом, требования, предъявляемые в инженерной практике к управляемым системам, математически записываются в виде ограничений на значения функционалов 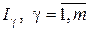 :
:
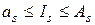 ,
, 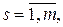 , (7.4)
, (7.4)
где 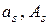 – заданные постоянные, равные граничным значениям изменения функционалов. В частности,
– заданные постоянные, равные граничным значениям изменения функционалов. В частности, 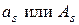 могут обратиться в бесконечность. При этом придем к односторонним ограничениям. Если
могут обратиться в бесконечность. При этом придем к односторонним ограничениям. Если 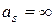 и
и 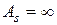 , то ограничения на критерий
, то ограничения на критерий 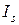 отсутствуют, и такой функционал из рассмотрения исключаем.
отсутствуют, и такой функционал из рассмотрения исключаем.
Под синтезом системы будем подразумевать нахождение таких значений управляющих параметров и функций, чтобы все функционалы 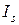 при всех режимах работы удовлетворяли ограничениям (7.4).
при всех режимах работы удовлетворяли ограничениям (7.4).
Если неравенства (7.4) выполняются, то система приемлема, если же нарушается хотя бы одно неравенство, система считается неудовлетворительной.
Обращаем внимание читателя, что в данном случае ни о какой оптимизации речь не идет.
Задача определения управления, гарантирующего выполнение ограничений, наложенных на значения функционалов, является типичной задачей проектирования, которую назовем основной задачей проектирования (ОЗП). Сформулируем ее так: среди допустимых управлений 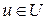 найти такое управление, при котором для системы (7.1), (7.2) выполнялись бы ограничения (7.4).
найти такое управление, при котором для системы (7.1), (7.2) выполнялись бы ограничения (7.4).
Надо отметить, что если ОЗП имеет решение, то обычно это решение не единственное, а целое множество решений, удовлетворяющих заданным требованиям. Это является важным обстоятельством, т.к. инженера не интересует только единственное решение задачи, которое практически невозможно абсолютно точно реализовать. Его интересует область значений параметров, множество решений, удовлетворяющих требованиям, предъявляемым к системе, что и дает решение ОЗП. Любое из полученных решений ОЗП является приемлемым. Это дает определенную свободу действий инженеру, которую он может использовать для введения некоторых изменений, возникающих в процессе проектирования или учета дополнительных требований, которые трудно формализовать. Имея свободу выбора значений параметров, т.е. неоднозначность решения основной задачи управления, можно просмотреть также различные оптимальные варианты управления, их расположение в области решений ОЗП. А окончательное решение принимают, имея перед собой полную картину возможных приемлемых решений.
Приведем геометрическую интерпретацию ОЗП. Пусть вектор управляющих параметров u и вектор-функционал I имеют по две компоненты: 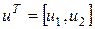 ,
, 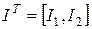 . Управление u может принимать свое значение из выпуклой области U, а вектор-функционал I – из прямоугольной области
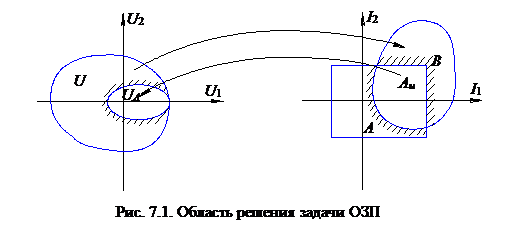
. Управление u может принимать свое значение из выпуклой области U, а вектор-функционал I – из прямоугольной области 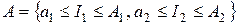 , рис. 7.1.
, рис. 7.1.
 |
Задаваясь всевозможными значениями
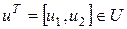 и используя уравнения процесса, построим некоторую область В (т.е. область U при отображении переходит в область В). Пересечение областей А и В, т.е. область
и используя уравнения процесса, построим некоторую область В (т.е. область U при отображении переходит в область В). Пересечение областей А и В, т.е. область 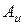 , представляет собой область выполнения ограничений на критерии I1, I2 при допустимых управлениях
, представляет собой область выполнения ограничений на критерии I1, I2 при допустимых управлениях 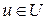 . При заданной области управления U реализуется только область значений критерия
. При заданной области управления U реализуется только область значений критерия 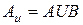 . Отыскивая область
. Отыскивая область 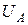 , которая согласно уравнениям и критериям системы отображается в область
, которая согласно уравнениям и критериям системы отображается в область 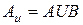 , получим все возможные решения основной задачи управления. Решение основной задачи управления сводится к построению области
, получим все возможные решения основной задачи управления. Решение основной задачи управления сводится к построению области 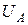 . Только при управлениях
. Только при управлениях 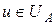 выполняются ограничения на критерии, т.е. система находится в области
выполняются ограничения на критерии, т.е. система находится в области 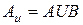 .
.
Дата добавления: 2019-09-30; просмотров: 616;











