Модель конвеерной обработки.

Средняя задержка команды на входе равна средней задержке команды на входе. Среднюю задержку (латентность) мы находим из графа переходов конвейера. Найдем нижнюю (L_min) и верхнюю (L_max) границу средней латентности (L).

Теорема: L_min£L£L_max, где L_max - число единиц в начальном векторе столкновений, а L_min находится из таблицы занятости - подсчитывается число меток в каждой строке и выбирается максимальное число.

Доказательство:

1) L_min£L. Пусть L - средняя латентность, тогда r=1/L - темп поступления или выдачи команд (количество инициаций). Введем к_i - коэффициент использования i ступени. Пусть d_i-число меток в i-ой строке. Оно характеризует, как использовать i-ый сегмент. 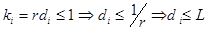будем считать, что это неравенство действует для любого числа i, т.е. 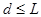, где

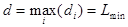
2) L£L_max. Докажем это утверждения для случая, когда граф состояний представляет собой простой, замкнутый цикл (простой цикл - это цикл в котором любое из состояний не повторяется). Докажем, что для такого цикла (жадная стратегия) L_max = числу единиц в начальном векторе столкновения. Рассмотрим модифицированный граф (только инициации). Обозначим за L₁ задержку при переходе от S₁ к S₂. L₁ - число единиц до первого нуля. В каждом состоянии существует свой вектор столкновения (S_i). Обозначим за L₁ задержку при переходе от S₁ к S₂. L₁ - число единиц до первого нуля. S₂ получается путем сдвига S₁ на L₁ позиций и прибавлением к нему начального вектора столкновений. Пусть x_i - число единиц в векторе столкновения, отвечающему i-ому состоянию. х - число единиц в начальном векторе столкновений.

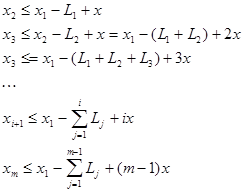
Замкнем круг

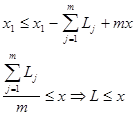
Что и требовалось доказать.