Расчет индуктивностей по заданной форме, размерам и взаимному расположению контуров.

Задавшись токами в рассматриваемых контурах, разбивают каждый из токов на элементарные нити тока и, пользуясь законом Био-Савара-Лапласса, определяют напряженность магнитного поля H в произвольно выбранной точке поля. Умножая H на магнитную проницаемость, предполагаемую одинаковой для проводов и окружающей их среды, получают магнитную индукцию B и, пользуясь формулой (1) Ф = 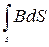, находят поток Ф, сцепляющийся с какой-нибудь нитью тока, после чего по формуле (2) Ψ = 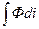вычисляют полный магнитный поток, сцепляющийся с рассматриваемым контуром. Подставляя найденное таким путем значение Ψ в формулу (3) или (4), получают выражение для собственной или соответственно взаимной индуктивности рассматриваемых контуров.

Однако в большинстве случаев для расчета индуктивностей пользуются другими формулами, в которых математические операции, необходимые для получения искомых величин (L или M), указаны явно. Разбив каждый из токов на элементарные нити тока, можно поток Ф, сцепляющийся с какой-нибудь нитью тока di^’, рассматривать как сумму потоков индукции, создаваемых другими нитями (di^’’), т.е. как сумму произведений вида 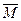di^’’, где 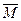- взаимная индуктивность нитей di’и di’’, причем это суммирование должно быть распространено на все нити данного контура при вычислении L и на все нити другого контура при вычислении М.

Таким образом, поток Ф выразится интегралом вида

Ф = ,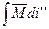

И, подставляя это выражение в (2), а (2) – в (3) и (4), можно написать

L = 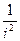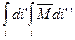(5);

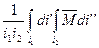M = (6);

Входящая в эти формулы взаимная индуктивность 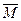двух нитей тока может быть найдена по формуле

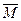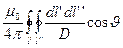= , (7)

где dl’ и dl” – элементы длины нитей l’ и l”; D – расстояние между этими элементами; 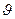- угол между ними, причем нити l’ и l” в формуле для собственной индуктивности принадлежат одному и тому же контуру, а в формуле для взаимной индуктивности – двум различным контурам.