Процесс переадресации виртуальной памяти
Процесс переадресацииопишем на примере микропроцессора 80386 фирмы Intel. Процесс переадресации показан на рис. 19 и 20.Перед исполнением загрузочные модели помещаются в оперативную память. Логические или виртуальные адреса, 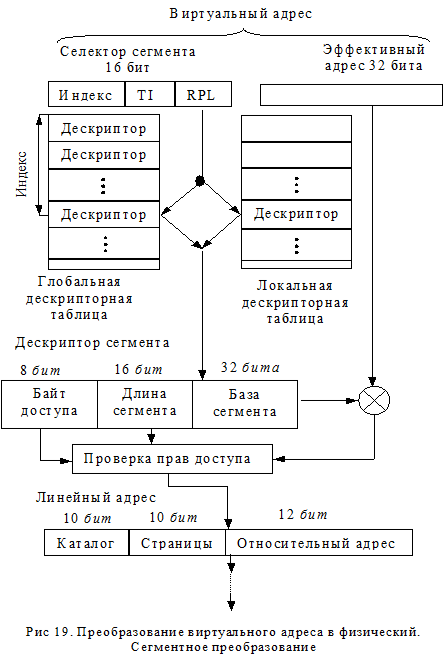
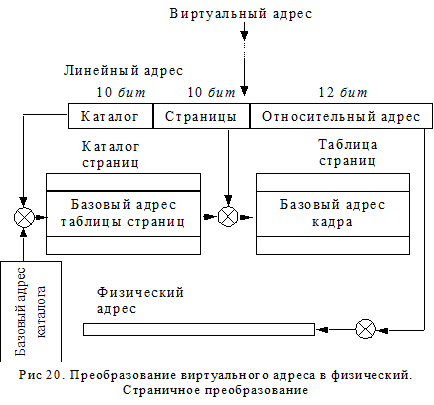 формируемые командами составляющими загрузочные модули, описывают положение адресуемых объектов в виртуальном адресном пространстве. Виртуальный адрес состоит из двух составляющих – селектора сегмента и эффективного адреса. Размер виртуального адреса 48 бит. Блок сегментации преобразует виртуальный адрес в линейный 32-х битный адрес. Блок управления страницами преобразует линейный адрес в физический адрес памяти.
формируемые командами составляющими загрузочные модули, описывают положение адресуемых объектов в виртуальном адресном пространстве. Виртуальный адрес состоит из двух составляющих – селектора сегмента и эффективного адреса. Размер виртуального адреса 48 бит. Блок сегментации преобразует виртуальный адрес в линейный 32-х битный адрес. Блок управления страницами преобразует линейный адрес в физический адрес памяти.
ФОРМАТЫ ДАННЫХ
Основными типами данных, которые встречаются при обработке информации в ЭВМ, являются числа, представленные в двоичной системе счисления, а также алфавитно-цифровые символы. Некоторые ЭВМ также осуществляют обработку чисел, представленных в двоично-десятичной системе счисления. Для записи и индикации адресов и данных могут применяться удобные и компактные восьмеричная и шестнадцатеричная системы счисления.
Минимальная хранимая единица данных в двоичной машине называется бит (от английского BInary digiT - двоичная цифра), совокупность из восьми битов называют байтом. В большинстве современных ЭВМ байт является минимально адресуемой порцией данных. В одном байте можно хранить числа от 0 до 28 -1 = 25510 или FF16. Для представления чисел с большим числом бит может использоваться несколько соседних байтов. Совокупность байтов, выделенную для хранения одной величины, называют полем. Адрес поля есть адрес его младшего байта. Остальные байты поля выбираются последовательно, путем увеличения адреса текущей ячейки памяти на 1. Биты внутри поля в большинстве ЭВМ нумеруют справа налево - 0,1,2,..n-1 (n - длина поля в битах).
Поле фиксированной длины считается выравненным на границу, если его адрес кратен длине. В некоторых типах ЭВМ поля должны быть обязательно выравнены. Так, в СМ ЭВМ шестнадцатибитное слово должно обязательно иметь четный адрес, и нарушение выравнивания приводит к прерыванию особого случая. Другие типы ЭВМ (например, персональные ЭВМ с процессорами семейства 80х86) не требуют обязательного выравнивания данных. Однако следует иметь в виду, что для считывания из памяти невыравненного шестнадцатибитного слова ЭВМ с процессором 8086 вынуждена автоматически генерировать два цикла считывания, а это приводит к резкому замедлению программ. В поле содержится некоторое двоичное число. Это число может быть командой или данными. Если число представляет собой данные, то оно может быть интерпретировано как: целое без знака, целое со знаком, двоично-десятичное число, дробное с точкой, вещественное в экспоненциальной форме (плавающая точка), последовательность символов (символьная строка).
Беззнаковое целое n-битное число X может принимать значения в диапазоне 0<=X<=2n -1, где n - количество бит в двоичном представлении числа (длина поля).
Для представления отрицательных чисел используется немодифицированный дополнительный код. Старший разряд является знаковым: 0 – плюс, 1 – минус. Диапазон чисел со знаком - от -2(n-1) до +2(n-1)-1. При этом признаком переполнения, например, при сложении двух чисел, в дополнительном коде является наличие переноса только в знаковый разряд из старшего разряда кода или только из знакового разряда кода.
Дополнительный код широко используется для представления положительных и отрицательных целых чисел. Можно представлять вещественные числа, полагая, что в n - битном поле существует двоичная точка (аналогичная десятичной точке). Например, вместо интерпретации 16-битного числа 00000000 011100012 как 11100012 = 11310, можно считать, что после третьего разряда справа находится двоичная точка и представлять это поле как 1110.0012 = 14.12510. При этом арифметические команды процессора будут давать правильные результаты, если во всех операндах (подразумеваемые) двоичные точки фиксированы в одном и том же месте. Такое соглашение называется представлением с фиксированной точкой. Недостаток такого представления – диапазон чисел от минимального до максимального слишком мал. Кроме того, такой способ представления вещественных чисел приводит к существенным трудностям программирования, так как нужно заставить компьютер следить за положением точки в числах. Несмотря на это, такое представление чисел широко применяется в тех случаях, когда требуется высокая скорость вычислений.
Одно из решений проблемы представления вещественных чисел состоит в масштабировании. К каждому числу присоединяется некоторый индикатор масштаба, который показывает положение двоичной точки в числе. Позиция точки может меняться от числа к числу, т. е. точка начинает “плавать” внутри числа. Таким образом, мы приходим к представлению чисел с плавающей точкой.
Представление числа с плавающей точкой (в экспоненциальной форме) имеет вид: Х = (-1)S * M * QP , где S - знак числа, M - мантисса, P - порядок, Q - основание системы счисления.
Знак числа 0 - плюс, 1 -минус. Положительные числа от отрицательных отличаются только знаком, дополнительный код не используется.
Основание системы счисления Q в большинстве ЭВМ равно 2, в некоторых ЭВМ (например, в IBM 360) Q=16.
Мантисса представлена в нормализованной форме. Для IBM PC мантисса в двоичном представлении имеет вид 1.q1q2q3q4q5..., где qi - двоичные цифры дробной части числа. Очевидно, что в этом случае 1 <= M < 2. Старший разряд мантиссы всегда равен 1, поэтому для экономии места в машинном представлении эту единицу можно не хранить.
В машинном представлении, как правило, вместо порядка хранится его характеристика Т, т.е. сумма истинного порядка и некоторой целой константы, называемой смещением, например, для IВМ РС смещение равно 127 и в поле порядка числа хранится Т = Р + 127, где Р - порядок. Такое представление порядков позволяет иметь положительные и отрицательные порядки.
На рис. 21 показано машинное представление числа с плавающей точкой в 4-байтовом поле. Такое представление числа обычно называют числом с одинарной точностью в отличие от числа с двойной точностью, которое имеет длину 8 байт
| разряды | 30 23 | 22 0 | |
| знак | характеристика | нормализованная мантисса |
Рис 21 Машинное представление числа с плавающей точкой
Число 1/32 = 1.0*2-5 в формате с одинарной точностью для IBM PC будет представлено так. Нормализованная мантисса равна 1.0, порядок равен -5, характеристика равна 127-5=122 десятичное или 0111 1010 двоичное. Старший бит мантиссы не хранится в целях экономии памяти. С учетом всего этого получаем число, изображенное на рис. 22.
| 0000000 00000000 00000000 | ||
| знак | характеристика | мантисса |
Рис. 22. Представление числа 1/32 в формате с одинарной точностью для IBM PC
Число с плавающей точкой, у которого в поле порядка и мантиссы содержатся нули, считается нулем.
Для представления алфавитно-цифровой информации, включающей в себя буквы алфавита, цифры, математические, пунктуационные и другие символы используются 7- и 8-битные символьные коды, наибольшее распространение получил 8-битный код ASCII (американский стандартный код обмена информацией).
Дата добавления: 2021-02-19; просмотров: 476;











