СПОСОБЫ ЗАДАНИЯ ПЛОСКОСТЕЙ
На чертеже плоскость может быть задана следующими способами:
1. тремя точками, не принадлежащими одной прямой (рис. 4.1, а);
2. прямой и точкой, не лежащей на ней (рис. 4.1, б);
3. двумя параллельными прямыми (рис. 4.1, в);
4. двумя пересекающими прямыми (рис. 4.1, г);
5. плоской геометрической фигурой (рис. 4.1, д);
6. следами.

| а) | б) | в) | г) | д) |
| Рис. 4.1 |
| а) | б) |
| Рис.4.2 |
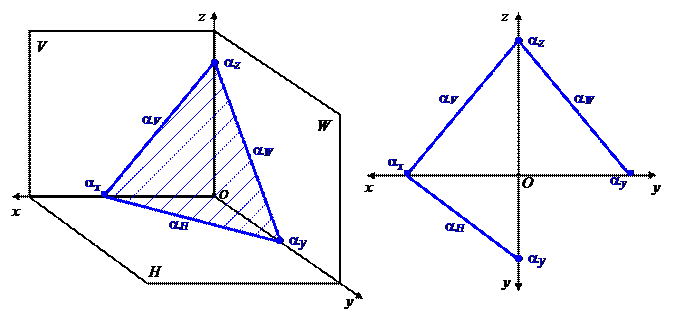 След плоскости- прямая, по которой пересекаются плоскость с плоскостями проекций (рис. 4.2).
След плоскости- прямая, по которой пересекаются плоскость с плоскостями проекций (рис. 4.2).
На рис. 4.2, а показано наглядное изображение плоскости a. Линию пересечения плоскости с горизонтальной плоскостью проекций называют горизонтальным следом плоскости (aН), с фронтальной - фронтальным следом плоскости (aV), с профильной - профильным следом плоскости (aW). Точки, в которых пересекаются два следа, называют точками схода следов (ax, ay, az). На рис. 4.2, б показано задание плоскости a следами на эпюре.
ПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ
Плоскость общего положения- это плоскость. не параллельная и не перпендикулярная ни одной из плоскостей проекций (рис. 4.1, 4.2).
ПЛОСКОСТИ ЧАСТНОГО ПОЛОЖЕНИЯ
Плоскость частного положения - это плоскость, параллельная или перпендикулярная какой либо плоскости проекций.
Плоскости уровня
Плоскость уровня- плоскость, параллельная какой-либо плоскости проекций и перпендикулярная двум другим плоскостям проекций.

Плоскость, параллельная горизонтальной плоскости проекций, называетсягоризонтальной плоскостью.
На рис. 4.3 плоскость, заданная треугольником ABC,является горизонтальной, т.к. ABC ║ H, ABC ^ V и W. А′В′С′ - натуральная величина треугольника.
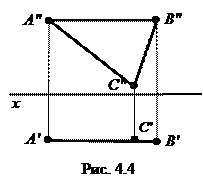
Плоскость, параллельная фронтальной плоскости проекций, называетсяфронтальной плоскостью.
На рис. 4.4 плоскость ABC является фронтальной, т.к. ABC ║ П2, ABC ^ П1 и П3. А″В″С″ - натуральная величина треугольника.
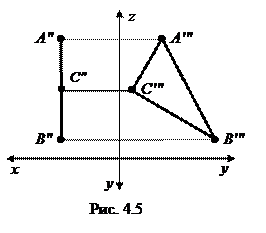
Плоскость, параллельная профильной плоскости проекций, называетсяпрофильной плоскостью.
На рис. 4.5 плоскость ABC является профильной, т.к. ABC ║ П3, ABC ^ П1 и П2. А″′В″′С″′ - натуральная величина треугольника.
Дата добавления: 2016-11-04; просмотров: 2192;











