ОРТОГОНАЛЬНЫЕ ПРОЕКЦИИ ТОЧКИ

Точка относится к основным, неопределяемым понятиям геометрии, она не имеет размеров.

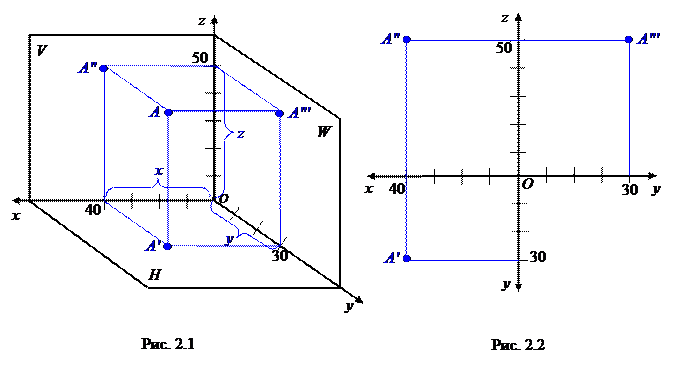
На рис. 2.1 показан I октант пространственной модели координатных плоскостей проекций. Положение точки в пространстве определяется координатами (х, у, z), показывающими величины расстояний, на которые точка удалена от плоскостей проекций. Чтобы определить эти расстояния, достаточно через точку А провести прямые, перпендикулярные к плоскостям проекций, определить точки встречи этих прямых с плоскостями проекций А', А", А'" и измерить величины отрезков [АА'], [АА"], [АА'"], которые укажут соответственно значения аппликаты z, ординаты у и абсциссы х точки А.

Точки А', А", А'" называют ортогональными проекциями точки А, при этом согласно принятым обозначениям:

А' – горизонтальная проекция точки А;

А" – фронтальная проекция точки А;

А'" – профильная проекция точки А.

Эпюр точки А показан на рис. 2.2. Отметим, что А' определяется координатами (х, у), А" (х, z), А'" (у, z). А' и А" находятся на одной вертикальной

линии связи, А" и А'" – на одной горизонтальной линии связи.

Таким образом, точка А находится в I октанте и имеет координаты (40, 30, 50). Она удалена от горизонтальной плоскости проекций на 50 мм, от фронтальной плоскости проекций - на 30 мм, от профильной плоскости проекций - на 40 мм.

На рис. 2.3 и 2.4 изображена точка В с координатами (40, 0, 30). Точка

В 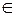V, удалена от горизонтальной плоскости проекций на 30 мм, от профильной плоскости проекций - на 40 мм