Логарифмические частотные характеристики систем

Амплитудно-фазовая частотная характеристика представляет собой выражение

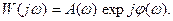(4.8)

Логарифмируя левую и правую части уравнения, найдем

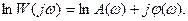(4.9)

Выражения lnA(ω) и φ(ω) представляют соответственно логарифмическую амплитудную (ЛАХ) и логарифмическую фазовую (ЛФХ) характеристики.

Для оценки отношения двух величин принято использовать логарифмическую единицу децибел (дБ). Связь между числом L и числом А дается формулой

L = 20lgA. (4.10)

Например, число А = 10 соответствует 20 дБ.

ПФ разомкнутых одноконтурных систем равна

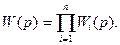(4.11)

Если представить в модулях и аргументах, т.е. в показательном виде, то

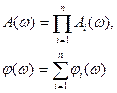
или в логарифмах

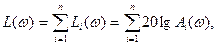(4.12)

где L(ω) – логарифмическая частотная характеристика разомкнутой системы.

Из этого выражения вытекает следующее правило построения ЛАЧХ разомкнутых систем: строят ЛЧХ отдельных звеньев и затем их графически складывают.

Например: пусть дана ПФ разомкнутой системы

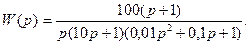
Подставив вместо р = jω и используя выражение (4.11), ЛАЧХ разомкнутой системы будет равна

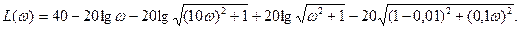
Асимптотическая ЛАЧХ состоит из четырех асимптот. Вычисляются сопрягающие частоты ω₁ = 1/10 = 0,1; ω₂ = 1; ω₃ = 1/0,1 = 10.

При частотах меньше сопрягающей частоты, под корнем оставляют только единицу (остальными членами пренебрегают).

Поэтому при ω < ω₁ L(ω) ≈ 40 – 20lg ω – уравнение первой асимптоты.

1). Первую асимптоту проводят до первой сопрягающей частоты ω₁ через точку с координатами ω₁ = 0,1 и L(ω) = 60 дБ с наклоном -20дБ/дек.

L(ω₁) = 40 – 20lg0,1 = 40 + 20 = 60 дБ.

2). Проводят вторую асимптоту от конца первой до второй сопрягающей частоты ω₂. Ее наклон определяется в зависимости от того, является ли ω₁ сопрягающей частотой форсирующего, апериодического или колебательного звеньев, т.е. +20, -20 или 40 дБ/дек. В данном случае ω₁ – сопрягающая частота апериодического звена, следовательно, наклон будет равен – 20дБ/дек.

При ω₁ ≤ ω < ω₂ уравнение второй асимптоты примет вид:

L(ω) ≈ 40 – 20lg ω – 20lg 10ω = 40 – 20lg ω – 20lg 10 – 20lg ω = 20 – 40lg ω.

3). Далее получают уравнение для третьей асимптоты аналогично второй.

Проводят третью асимптоту от конца второй до третьей сопрягающей частоты ω₃, наклон которой будет равен +20 дБ – форсирующее звено при ω₂.

При ω₂ ≤ ω < ω₃ уравнение третьей асимптоты примет вид

L(ω) ≈ 20 – 40lg ω + 20lg ω = 20 - 20lg ω.

4). Проводят четвертую асимптоту от конца третьей сопрягающей частоты ω₃ с наклон равным - 40 дБ – колебательное звено при ω₃.

При ω ≥ ω₃ уравнение третьей асимптоты примет вид

L(ω) ≈ 20 – 20lg ω - 40lg 0,1ω = 20 - 20lg ω - 40lg 0,1 - 40lg ω = 60 - 60lg ω.

ЛАЧХ разомкнутой системы примет вид, приведенный на рисунке 4.4.

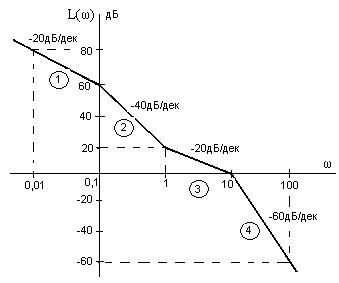
Рисунок 4.4 – ЛАЧХ разомкнутой системы