ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА МЕТОДОМ МАГНЕТРОНА

Основные понятия

При движении электрона в электрическом и магнитном полях траектория электрона определяется величиной и направлениями этих полей.

Существует несколько методов определения удельного заряда электрона, одним из них является метод магнетрона. Это название связано с тем, что применяемая в работе конфигурация электрического и магнитного полей напоминает конфигурацию полей в магнетронах - генераторах электромагнитных колебаний в области сверхвысоких частот. Магнетроны, в частности, применяются во всех бытовых микроволновых печах.

В нашем случае движение электронов происходит в пространстве, заключённом между катодом и анодом вакуумного диода. Катод и анод представляют собой плоскопараллельные пластины. Диод помещен внутри соленоида (катушка с большим количеством витков провода), создающего магнитное поле с вектором индукции, параллельным плоскости пластин (рис.1).

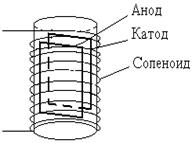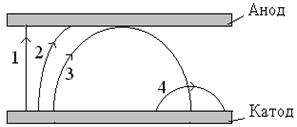Рис.1. Рис. 2.

Рассмотрим возможный вид траектории электронов при различных условиях (рис. 2 – вид на электроды вдоль их оси). Положим, что магнитное поле отсутствует (В = 0) – траектория 1. В этом случае электроны, вылетевшие из катода, движутся прямолинейно перпендикулярно аноду с постоянным ускорением. Влиянием на движение электронов объемного заряда (см. работу № 2) пренебрегаем. Положим, что электрон вылетел из катода с нулевой начальной скоростью. Тогда его скорость при попадании на анод v можно найти из закона сохранения энергии , где U – разность потенциалов между катодом и анодом, которая создаёт электрическое поле (рис.2), m - масса электрона, а е - заряд электрона. Получаем:

(1)

Теперь положим, что электрическое поле отсутствует, имеется магнитное поле с индукцией В, а электроны вылетают из катода со скоростью V, направленной перпендикулярно катоду. Со стороны магнитного поля на электроны будет действовать сила Лоренца

Для рассматриваемого случая F = e×V×B, и сила Лоренца сообщает электрону центростремительное ускорение, то есть он будет двигаться по дуге окружности, радиус которой зависит от величины В (траектории 2 – 4, где B₂< B₃< B₄). Согласно второму закону Ньютона

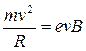
(3)

откуда

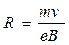
(4)

При всех величинах В, превышающих некоторую критическую В_КР (ей соответствует траектория 3), электроны на анод, очевидно, не попадут (траектория 4). Не долетая до анода, они будут возвращаться на катод, скорость их при этом будет уменьшается, т. к. на своём пути к катоду они будут двигаться в задерживающем электрическом поле. Из рисунка видно, что радиус траектории, соответствующей критической индукции, равен L, где L – расстояние между анодом и катодом. При В < В_КР, все электроны попадают на анод.

В действительном случае, при наличии одновременно электрического и магнитного полей и нулевой начальной скорости электронов, траектория их – это некоторая достаточно сложная кривая с увеличивающимся по мере приближения к аноду радиусом кривизны. Особенностью метода магнетрона является то, что конкретный вид всей траектории нас не интересует. Так как магнитное поле не изменяет модуля скорости, то вблизи анода он остается равным v из формулы (1).

Из вышеуказанного следует, что зависимость величины анодного тока I_A от величины индукции должна быть следующей: при любой индукции, меньшей критической, ток постоянен, при всех значениях индукции, больших или равном критическому, ток равен нулю (рис. 3, прерывистая линия).

Рис. 3.

Таким образом, измеряя ток при различных значениях индукции, можно найти критическое значение В_KP.

Приняв В = В_КР, R = L и подставляя v из (1) в (4)

(5)

Формула (5) позволяет определить 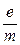, если при заданном потенциале анода Uнайдено значение магнитного поля В_KP,при котором электроны перестают попадать на анод. Более строгий расчет приводит к такой же формуле.

До сих пор мы предполагали, что все электроны покидают катод с нулевой скоростью. В этом случае при B< B_KP все электроны без исключения попадали бы на анод, а при B> B_KP все они возвращались бы на катод, не достигнув анода. На самом деле, электроны, испускаемые нагретым катодом, обладают различными начальными скоростями. Критические условия достигаются, поэтому, для разных электронов при разных значениях В. Поэтому кривая зависимости I_A (B) приобретает вид сплошной линии (рис.3).

Кроме того, реальная геометрия электродной системы отличается от от рассмотренной идеальной, поэтому для электронов, вылетающих из разных точек поверхности анода, величина L может несколько отличаться. Эти причины приводят к дополнительному сглаживанию кривой I_A (B). Поэтому в формулу (5) вводится конструктивный коэффициент К, который учитывает дополнительно и другие конструктивные особенности лабораторной установки:

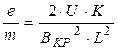
(6)

Выше было сказано, что строго вертикального спада анодного тока при В_КР наблюдаться не будет, т. к. более медленные электроны перестанут доходить до анода при меньшем В, а затем быстрые электроны при большем В. Поэтому правильно будет значение В_КР брать из средней части крутого спада “сбросовой” характеристики - это будет соответствовать средним скоростям электронов (рис.3).

В лабораторной установке измеряется не индукция магнитного поля В, а ток в катушке (соленоиде) I_С, который связан с индукцией формулой бесконечно длинного соленоида

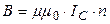
(7)

где n - число витков на 1 м соленоида, m = 1, m₀ = 4p ×10^-7 Гн/м – магнитная постоянная. Для используемой установки n = (230 ± 2) × 10 ². I_С пропорционален В, поэтому качественно вид зависимости I_A от I_C будет таким же, как и I_A от В (рис. 4).

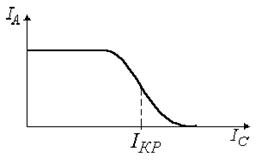
Рис.4

Окончательная формула для расчета удельного заряда электрона получается при подстановке (7) в (6):

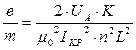
(11)