Линейные операции над векторами. Базис. Разложение вектора по базису. Деление отрезка в данном отношении

1. Величины, которые характеризуются только численными значениями, называются скалярными, например, площадь, длина, объем, температура, масса.

В математике и ее приложениях: физике, механике, геометрии и т.д. рассматривают векторные величины, которые определяются не только своим численным значением, но и направлением. Например, сила, скорость, ускорение и т.д.

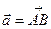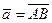Вектор - это направленный отрезок прямой, т.е. отрезок, имеющий определенную длину и направление. Если А - начало вектора, а В - его конец, то вектор обозначают символом и или . Геометрически вектор изображают в виде стрелки, направленной от А к В: .

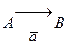Длиной или модулем вектора 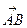называется длина отрезка между точками А и В и обозначается 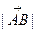, 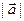или просто АВ.

Вектор, для которого А=В, называется нулевым и обозначается .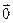

Если 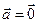, то 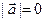и наоборот, если 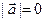, то .

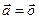Вектор, для которого длина равна 1, называется единичным и обозначается , .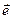

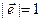Вектор 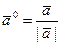, , 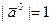называется ортом вектора .

Вектор 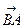называется противоположным вектору 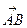и обозначается - .

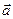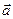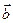Векторы и , параллельные друг другу, называются коллениарными; записывают .

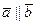Векторы, расположенные в одной плоскости или параллельных плоскостях, называют компланарными.

Определение. Два вектора и 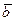считают равными, 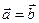, если

1) ,

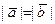2) 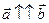, т.е. 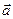и 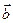коллинеарны и сонаправлены.

Равные векторы можно совместить друг с другом параллельным переносом, т.е. безразлично, где поместить начало вектора. Такие векторы поэтому называют свободными.

Из определения следует, что 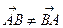или .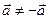

В силу того, что рассматриваются свободные векторы, любые компланарные векторы можно считать расположенными в одной плоскости. Если среди трех векторов один нулевой или два коллинеарны, то такие векторы компланарны.

2. Линейными операциями над векторами называют 1) операции (действия) сложения векторов и 2)умножения вектора на число (скаляр).

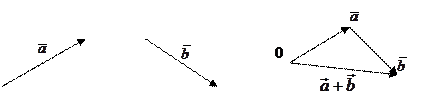Пусть и 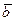- векторы. Суммой векторов и 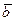называется вектор 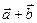, который начало первого вектора соединяет с концом второго вектора 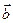(правило треугольника):

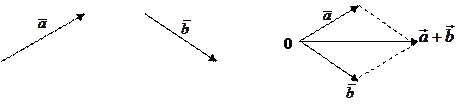Векторы 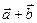можно получить также по правилу параллелограмма:

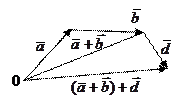Используя определение суммы двух векторов (правило треугольника), можно получить сумму трех и более векторов:

Под разностью векторов и 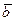понимается вектор / :

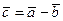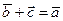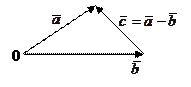
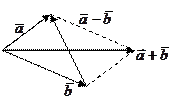В параллелограмме, построенном на векторах и 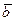, вектор 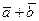направлен по одной диагонали (главной), а 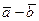- по второй:

Произведением вектора на число 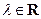называется вектор :

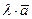1) ,

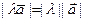2) 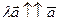, l>0,

3) 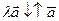, l<0.

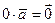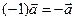При этом для любого вектора , а и .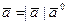

Ясно, что линейные операции над векторами обладают следующими свойствами:

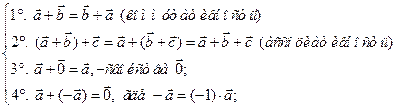
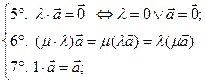(1)

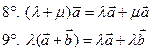- дистрибутивные законы.

3. Вектор 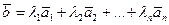, , 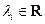, 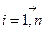называется линейной комбинацией векторов , .

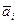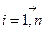Если 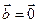при условии, что 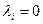, , 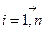то векторы 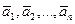называют линейно независимыми, а если 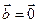и хотя бы одно из чисел 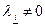, , 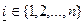то векторы 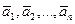называют линейно зависимыми.

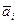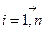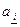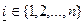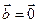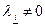Если векторы , , линейно зависимы, то один из векторов , есть линейная комбинация остальных. Действительно, если , а , то

,

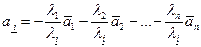обратно, если один из векторов 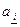есть линейная комбинация остальных, то 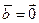, где 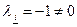, т.е. 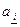, 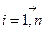- линейно зависимые векторы.

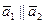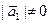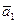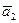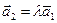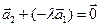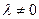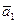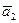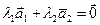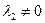Если , , то и - линейно зависимы, так как , и, следовательно, , где . Обратно, если и - линейно зависимые, т.е. , где , то 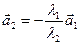, и потому 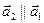. Таким образом, два вектора 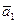и 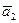в плоскости Е² линейно независимы тогда и только тогда, когда ∦ .

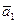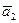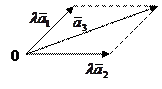Рассмотрим систему из трех векторов 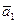, , 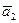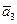в пространстве Е³, и пусть 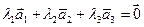, где 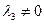. Тогда 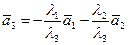, т.е. 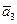комланарен с 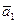и 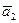. обратно, если три вектора 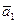, , 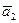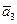комланарны, то один из них есть линейная комбинация остальных, например, 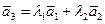. Отсюда получаем, что 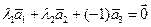, т.е. 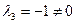, и потому векторы 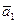, , 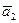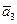- линейно зависимы.

Таким образом, три вектора 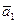, , 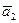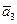в Е³ линейно зависимы тогда и только тогда, когда они не комланарны.

Базисом называется система из n линейно независимых единичных векторов 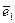, , 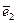…, , , 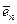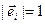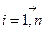. Базис обозначается ( 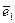, , 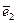…, 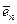). Число n - называют размерностью базиса. Оно совпадает с размерностью Еⁿ. Базисом на плоскости Е² является упорядоченная пара ( 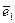, 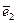), где 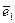∦ 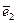, а базисом в пространстве Е³ является упорядоченная тройка ( 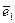, , 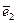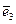), не коллинеарных векторов , , .

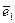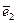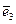Для произвольного вектора в базисе ( 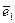, , 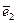…, 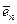) имеем разложение, так как 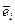- линейно независимые:

, , ,

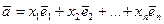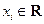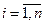где числа x_i называют координатами вектора в базисе ( 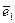, , 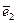…, 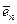). Координаты x_i, 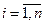, вектора в базисе ( 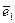, , 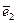…, 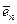) определены однозначно. В самом деле, пусть существуют другие координаты 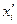, , 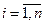вектора в том же базисе. Тогда имеем равенство

.

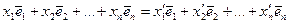Откуда следует

.

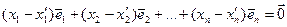Так как векторы 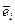, 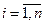- линейно независимые, то 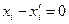, т.е. 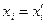, 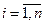. Однозначность координат вектора в базисе ( 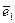, …, 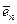), таким образом доказана.

Отсюда следует, что при выбранном базисе ( 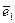, , 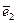…, 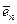) каждой упорядоченной системе координат 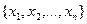соответствует единственный вектор 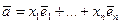. Поэтому вектор записывают в виде .

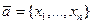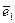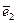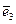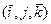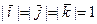В пространстве Е³ в качестве базиса ( , , ) используют ортонормированный базис , где и 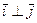, , 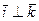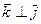. В этом случае координаты вектора носят специальное обозначение: .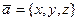

Пусть

,

.

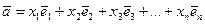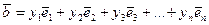Тогда в силу свойств (1) линейных операций над векторами получим

,

.

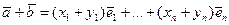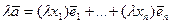Таким образом, при линейных действиях над векторами соответствующие действия производятся над их координатами.

В частности, если 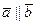, то 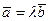, т.е. .

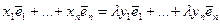Отсюда в силу линейной независимости векторов 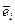, , 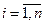следует, что

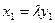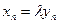, …, , т.е.

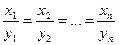. (2)

Это есть условие коллениарности векторов и 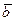в Еⁿ в координатной форме.

Декартовой системой координат называется совокупность из точки 0, называемой началом координат, и базиса, т.е. .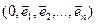

* Система координат 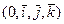в Е³ называется декартовой прямоугольной системой координат. Векторы 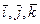направлены вдоль осей Ox - абсцисс, ординат Oy и аппликат Oz, соответственно:

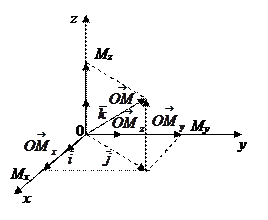Соединяя начало координат О с точкой 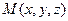, получим вектор 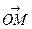, который называется радиусом-вектором точки М. Его координаты совпадают с координатами точки М, так как 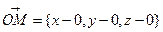={x,y,z} или

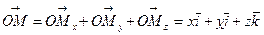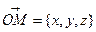® , где 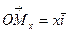, , 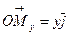, 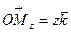так как 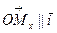и 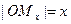,и т.д.

Если в прямоугольной декартовой системы координат (д.с.к.) 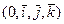дан вектор 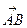, то 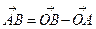. Учитывая, что 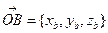, 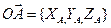и применяя правило действий над векторами в координатной форме, получим

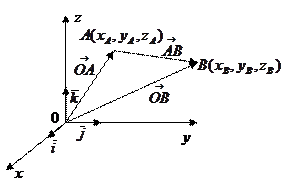
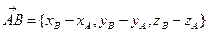. (3)

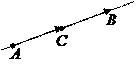4. Пусть дан отрезок 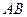в Е³. Если точка С делит отрезок АВ в отношении l, т.е.

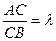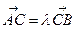, то (4)

так как .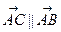

По формуле (3) имеем:

,

.

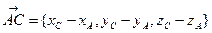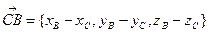Отсюда и из (4) получаем

,

,

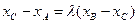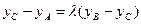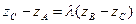
и потому

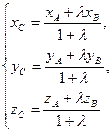(5)

- формулы деления отрезка в отношении l.

Если 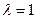, то из (5) находим координаты середины отрезка AB:

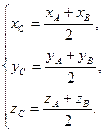(6)

Скалярное произведение двух векторов и его свойства. Модуль вектора. Расстояние между двумя точками. Угол между векторами. Условие ортогональности двух векторов. Проекция вектора на направление другого вектора

Определение. Скалярным произведением векторов и 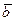называется число, обозначаемое 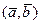, 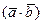или 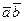и определяемое равенством

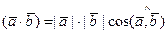, (7)

где 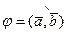- угол между векторами и , .

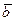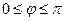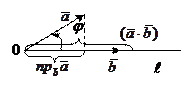Определение. Проекцией вектора на ось l вектора 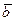называется скалярная величина

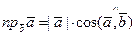, (8)

при этом 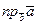>0, есл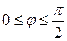и , и 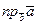<0, есл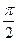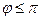и < , и 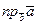=0, когда .

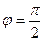Из (7) и (8) получаем, что

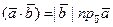. (9)

Скалярное произведение обладает следующими свойствами:

1°. 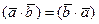- симметричность.

2°. 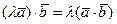- сочетательность относительно .

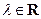3°.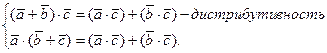

4°. 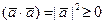, причем .

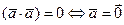5°. , , .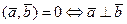

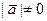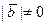Эти свойства очевидны и легко доказываются с учетом (7) и (9), Например,

.

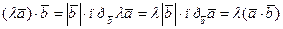Из 5° и 4° в частности следует, что

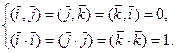(10)

Из (9) получим, что

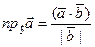. (11)

Рассмотрим вектор

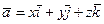(12)

в прямоугольной д.с.к. 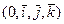. Так как 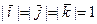, то из (11) находим

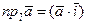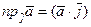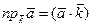, , . (13)

Умножим обе части равенства (12) скалярно на векторы 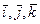. С учетом 1°-5° и (10) получим

,

,

.

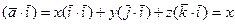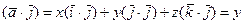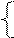
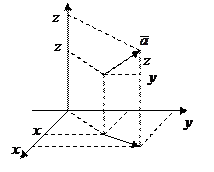
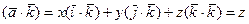Поэтому

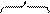
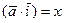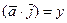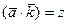, , . (14)

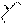Из (13) и (14) вытекает, что

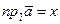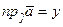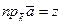, , . (15)

Обозначим углы вектора с осями Ox, Oy, Oz через a, b, g соответственно. Тогда из (8) и (15) следует

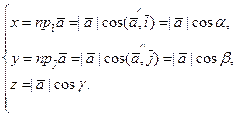(16)

Из (16) находим

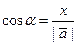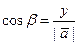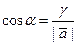, , . (17)

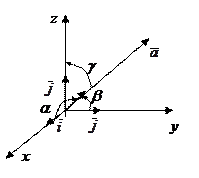Числа cosa, cosb, cosg называют направляющими косинусами вектора .

Пусть даны два вектора 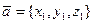и 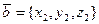в д. пр. с.к. 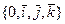. Тогда с учетом 1°-5° и (10) имеем

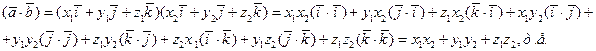
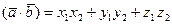(18)

- координатная форма скалярного произведения.

Таким образом, скалярное произведение двух векторов равно сумме произведений их одноименных координат.

Условие ортогональности 5° двух векторов в координатной форме с учетом (18) запишется в виде

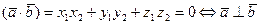. (19)

Из (18) следует, что

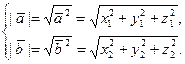(20)

Тогда из (7), (19) и (20) следует, что угол 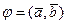между векторами находится по формуле

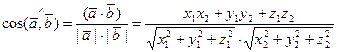, (21)

а из (17) и (20) находим

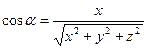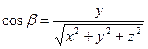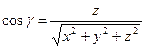, , . (22)

Из (22) получается соотношение между направляющими косинусами

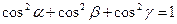, (23)

т.е. сумма квадратов направляющих косинусов вектора , , 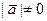равна единице, т.е. .

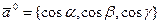Из (8) и (21) находим

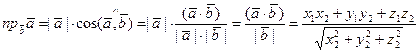. (24)

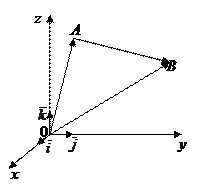Пусть даны две точк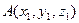и и 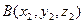. Найдем расстояние АВ между ними. Имеем 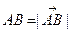. Так как 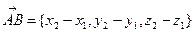, то из (20) следует, что

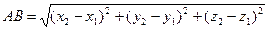. (25)