Уравнение состояния идеального газа (уравнение Менделеева - Клапейрона).

До этого рассматривались газовые процессы, при которых один из параметров состояния газа оставался неизменным, а два других изменялись. Теперь рассмотрим общий случай, когда изменяются все три параметра состояния газа и получим уравнение, связывающее все эти параметры. Закон, описывающий такого рода процессы, был установлен в 1834г. Клапейроном (французский физик, с 183г. работал в Петербургском институте путей сообщения) путем объединения рассмотренных выше законов.

Пусть имеется некоторый газ массой “m”. На диаграмме (P, V) рассмотрим два его произвольных состояния, определяемых значениями параметров P₁, V₁, T₁ и P₂, V₂, T₂. Из состояния 1 в состояние 2 будем переводить газ двумя процессами:

1. изотермического расширения (1®1¢);

2. изохорического охлаждения (1¢®2).

Первый этап процесса описывается законом Бойля-Мариотта, поэтому

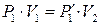. (9.5)

Второй этап процесса описывается законом Гей-Люссака:

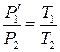. (9.6)

Исключая из этих уравнений 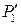, получим:

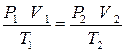. (9.7)

Поскольку состояния 1 и 2 были взяты совершенно произвольно, то можно утверждать, что для любого состояния:

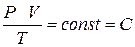
– уравнение Клапейрона

где С – постоянная для данной массы газа величина.

Недостатком этого уравнения является то, что величина “C” различна для различных газов, Для устранения этого недостатка Менделеев в 1875г. несколько видоизменил закон Клапейрона, объединив его с законом Авогадро.

Запишем полученное уравнение для объема V_км. одного 1 киломоля газа, обозначив постоянную буквой “R”:

.

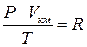Согласно закону Авогадро при одинаковых значениях P и T киломоли всех газов будут иметь одинаковые объемы V_км. и, следовательно, постоянная “R” будет одинакова для всех газов.

Постоянная “R”называется универсальной газовой постоянной. Полученное уравнение 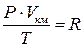связывает параметры киломоля идеального газа и, следовательно, представляет уравнение состояния идеального газа.

Значение постоянной “R” можно вычислить:

.

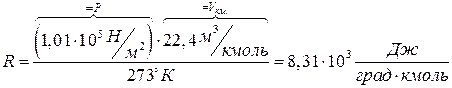От уравнения для 1кмоль легко перейти к уравнению для любой массы газа “m”, приняв во внимание, что при одинаковых давлениях и температуре “z” киломолей газа будут занимать в ”z” раз больший объем, чем 1 кмоль. (V=z×V_км.).

С другой стороны отношение 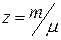, где m – масса газа, m – масса 1 кмоля, будет определять число молей газа.

Умножим обе части уравнения Клапейрона на величину 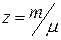, получим

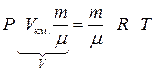Þ 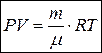(9.7а)

Это и есть уравнение состояния идеального газа, записанное для любой массы газа.

Уравнению 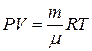можно придать другой вид. Для этого введем величину

,

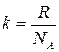где R – универсальная газовая постоянная;

N_A – число Авогадро;

k – постоянная Больцмана (далее будет показано, что “k” представляет коэффициент пропорциональности между средней энергией теплового движения молекулы и абсолютной температурой).

Подстановка числовых значений R и N_A дает следующее значение:

.

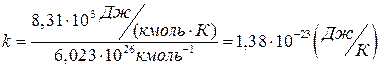Умножим и разделим правую часть уравнения 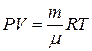на N_A, тогда 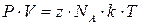, здесь 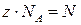– число молекул в массе газа “m”.

С учетом этого

(*)

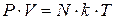Вводя величину 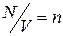– число молекул в единице объема, приходим к формуле:

(**)

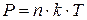Уравнения (*) и (**) представляют различные формы записи уравнения состояния идеального газа.

Отношение 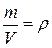, тогда плотность идеального газа можно получить из уравнения .

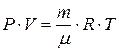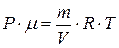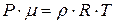Þ Þ .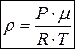

Таким образом, плотность идеального газа пропорциональна давлению и обратно пропорциональна температуре.

Простая связь между температурой и остальными параметрами идеального газа делает заманчивым его использование в качестве термометрического вещества. Обеспечив постоянство объема и использовав в качестве температурного признака давление газа, можно получить термометр с идеальной линейной температурной шкалой. Эту шкалу будем называть идеальной газовой шкалой температур.

Практически, по международному соглашению, в качестве термометрического тела берут водород. Установленная по водороду с использованием уравнения состояния идеального газа шкала называется эмпирической шкалой температур.