Вынужденные колебания. Резонанс.

Для того чтобы система совершала незатухающие колебания, необходимо извне восполнять потери энергии колебаний на трение. Для того, чтобы энергия колебаний системы не убывала обычно вводят силу, периодически воздействующую на систему (такую силу будем называть вынуждающей, а колебания вынужденными).

ОПРЕДЕЛЕНИЕ: вынужденными называются такие колебания, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы.

Эта сила, как правило, выполняет двоякую роль:

во-первых, она раскачивает систему и сообщает ей определенный запас энергии;

во-вторых, она периодически восполняет потери энергии (расход энергии) на преодоление сил сопротивления и трения.

Пусть вынуждающая сила изменяется со временем по закону:

.

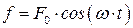Составим уравнение движения для системы, колеблющейся под воздействием такой силы. Предполагаем, что на систему также действует квазиупругая сила 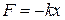и сила сопротивления среды 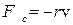(что справедливо в предположении малости колебаний). Тогда уравнение движения системы будет иметь вид:

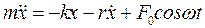или .

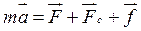Проведя подстановки 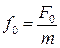, , 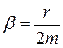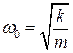– собственная частота колебаний системы, получим неоднородное линейной дифференциальное уравнение 2^го порядка:

.

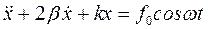Из теории дифференциальных уравнений известно, что общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения.

Общее решение однородного уравнения известно:

,

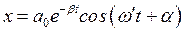где 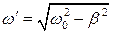; a₀ и a – произвольные const.

Далее предположим, что частное (не содержащее произвольных констант) решение неоднородного уравнения имеет вид

.

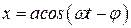С помощью векторной диаграммы можно убедиться, что такое предположение справедливо, а также определить значения “a” и “j”.

Амплитуда колебаний определяется следующим выражением:

.

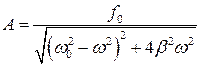Значение “j”, которое представляет собой величину отставания по фазе вынужденного колебания 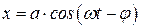от обусловившей его вынуждающей силы 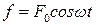, также определяется из векторной диаграммы и составляет:

.

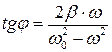Окончательно, частное решение неоднородного уравнения примет вид:

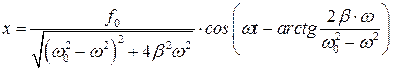
(8.18)

Эта функция в сумме с

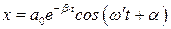
(8.19)

дает общее решение неоднородного дифференциального уравнения, описывающего поведение системы при вынужденных колебаниях. Слагаемое (8.19) играет заметную роль в начальной стадии процесса, при так называемом установлении колебаний (рис. 8.10). С течением времени из-за экспоненциального множителя 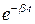роль второго слагаемого (8.19) все больше уменьшается, и по прошествии достаточного времени им можно пренебречь, сохраняя в решении лишь слагаемое (8.18).

Таким образом, функция (8.18) описывает установившиеся вынужденные колебания. Они представляют собой гармонические колебания с частотой равной частоте вынуждающей силы. Амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы. Для данной колебательной системы (определенных w₀ и b) амплитуда зависит от частоты вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания “j” также зависит от частоты вынуждающей силы.

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Колебательная система оказывается особенно отзывчивой на действие вынуждающей силы при этой частоте. Это явление называется резонансом, а соответствующая частота – резонансной частотой.

ОПРЕДЕЛЕНИЕ: явление, при котором наблюдается резкое возрастание амплитуды вынужденных колебаний, называется резонансом.

Резонансная частота определяется из условия максимума для амплитуды вынужденных колебаний:

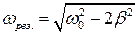. (8.20)

Тогда, подставив это значение в выражение для амплитуды, получим:

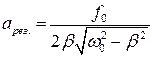. (8.21)

При отсутствии сопротивления среды амплитуда колебаний при резонансе обращалась бы в бесконечность; резонансная частота при тех же условиях (b=0) совпадает с собственной частотой колебаний.

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы (или, что то же самое, от частоты колебаний) можно представить графически (рис. 8.11). Отдельные кривые соответствуют различным значениям “b”. Чем меньше “b”, тем выше и правее лежит максимум данной кривой (см. выражение для w_рез.). При очень большом затухании 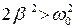резонанс не наблюдается – с увеличением частоты амплитуда вынужденных колебаний монотонно убывает (нижняя кривая на рис. 8.11).

Совокупность представленных графиков, соответствующих различным значениям b, называется резонансными кривыми.

Замечания по поводу резонансных кривых:

при стремлении w®0 все кривые приходят к одному, отличному от нуля значению, равному 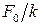. Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы F₀.

при w®¥ все кривые асимптотически стремятся к нулю, т.к. при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместится из положения равновесия.

чем меньше b, тем сильнее изменяется с частотой амплитуда вблизи резонанса, тем «острее» максимум.

Примеры:

С явлением резонанса приходится считаться при конструировании машин, механизмов и сооружений (мосты, самолеты, корабли и т.п.).

Явление резонанса часто оказывается полезным, особенно в акустике и радиотехнике.