Скорость, ускорение и энергия колеблющегося тела.

Вернемся к формулам для смещения x, скорости v и ускорения a гармонического колебательного процесса.

Пусть имеем тело массы «m», которое совершает под действием квазиупругой силы колебания по закону:

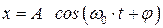, тогда

.

.

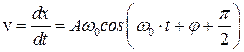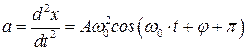Видно, что скорость и ускорение также изменяются по гармоническому закону (графики приводились ранее) с периодом колебаний равным T. Из сравнения формул видно, что скорости v опережает смещение по фазе на 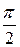. Это означает, что если x=0, то v тела имеет максимальное значение .

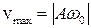Для ускорения зависимость иная. В каждый момент времени ускорение пропорционально смещению и находится с ним в противофазе. Это означает, что когда x=x_max, то ускорение тоже максимально, но отрицательно, т.е. при x=x_max, 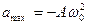(графики приведены ранее).

Квазиупругая сила, под действием которой происходит колебательное движение, является консервативной. Поэтому полная энергия гармонического колебательного движения должна оставаться постоянной. В процессе колебаний происходит превращение кинетической энергии в потенциальную и обратно (силами сопротивления пренебрегаем). Причем в моменты наибольшего отклонения о положения равновесия 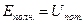, причем 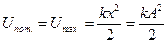; при прохождении положения равновесия 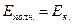, причем 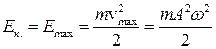. Так как 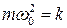, то .

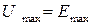Определим, как со временем изменяется Е_к и U_п для гармонического колебания 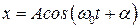. Имеем

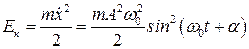(8.4)

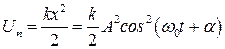(8.5)

Т.к. 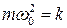, то имеем

,

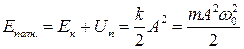т.е. 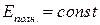как и должно было быть, т.к. квазиупругая сила – консервативная сила.

Используя формулы тригонометрии, можно получить выражения для

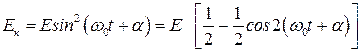(8.6)

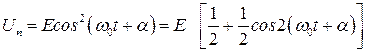(8.7)

Здесь E – полная энергия системы. Из формул видно, что Е_к и U_п изменяются с частотой 2w₀, т.е. с частотой вдвое превышающей частоту гармонического колебания. Среднее значение квадрата sin и квадрата cos равно 1/2. Следовательно, среднее значение E_к совпадает со средним значением U_п и равно E/2.