Интервал между событиями.
В теории относительности вводят понятие события, которое определяется местом, где оно произошло, и временем, когда оно произошло. Событие можно изобразить точкой в воображаемом четырехмерном пространстве, на осях которого три пространственные координаты и время. Эти точки называются мировыми точками. Всякой частице соответствует некоторая линия (мировая линия).
В классической физике при переходе от одной системы координат к другой координаты точек изменяются, но неизменным остается расстояние между двумя выбранными точками Dl, которое можно определить из формулы Dl2 = (x2 - x1 )2 + (y2 -y1)2 + (z2 - z1 )2, где x1 , y1 , z1 , x2 , y2 , z2 - координаты точек. В теории относительности при переходе от одной системы к другой расстояние между точками не остается постоянным, т.е. не является инвариантом. Инвариантом, не зависящим от выбранной системы координат, является интервал между событиями Ds, который определяется по формуле Ds2 = c2t2 - Dl2 . С формальной математической точки зрения интервал можно рассматривать как расстояние между мировыми точками в воображаемом четырехмерном пространстве.
Если Ds2 > 0, то интервал называют времениподобным,и существует такая система отсчета. в которой оба события произошли в одной точке. Два события могут быть причинно связаны друг с другом только в том случае, если интервал между ними времениподобный.
Если Ds2 < 0, то интервал называют пространственноподобным,и сущес-твует такая система отсчета, в которой оба события произошли в одно и тоже время.
Теория относительности сформулировала новое представление о пространстве и времени, показав, что пространство и время органически связаны между собой и образуют единую форму существования материи. Дальнейшее развитие теории относительности (общая теория относительности) показало, что свойства пространства-времени определяются действующими в данной области полями тяготения, и изменяются в зависимости от концентрации в пространстве массы вещества.
| ЛЕКЦИЯ 10 |
Колебания.
Общие сведения.
Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости или такое движение, при котором система многократно отклоняясь от своего состояния равновесия, каждый раз вновь возвращается к нему. Если этот возврат осуществляется через равные промежутки времени, то колебания называются периодическими.
В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические и т.д. Здесь мы будем рассматривать механические колебания.
Колебания широко распространены в природе и технике. Во многих случаях они играют отрицательную роль (колебания моста, вибрации корпуса корабля, вибрации крыльев самолета и т.п.). В подобных случаях задача состоит в том, чтобы предотвратить возникновение колебаний.
Вместе с тем колебательные процессы лежат в самой основе различных отраслей техники. Так, например, на колебательных процессах основана вся радиотехника.
 ПРИМЕРЫ колебательных движений: вибрация струны, движение поршня, суточные и годичные изменения температуры воздуха, морские приливы-отливы, биение сердца, тепловое движение ионов кристаллической решетки твердого тела, переменный ток и его электромагнитное поле, движение электронов в атоме и т.д.
ПРИМЕРЫ колебательных движений: вибрация струны, движение поршня, суточные и годичные изменения температуры воздуха, морские приливы-отливы, биение сердца, тепловое движение ионов кристаллической решетки твердого тела, переменный ток и его электромагнитное поле, движение электронов в атоме и т.д.
Всевозможные колебательные движения имеют два общих характерных признака:
1. До начала колебаний и после их окончания тело находится в положении равновесия;
2. Наличие силы, которая возникает, как только тело выходит из положения равновесия. Эта сила пропорциональна смещению и направлена в сторону, противоположную смещению тела (направлена к положению равновесия). Для такой силы справедливо 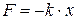 . Называется такая сила упругой силой. Под действием такой силы, например, может сжиматься и разжиматься пружина.
. Называется такая сила упругой силой. Под действием такой силы, например, может сжиматься и разжиматься пружина.
Но может случиться, что сила иного происхождения обнаруживает такую же закономерность.
Рассмотрим колебания математического маятника (рис. 8.1).
Отклоним маятник на некоторый угол j от положения равновесия и разложим силу тяжести 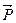 на две составляющие:
на две составляющие:
- Pt – перпендикулярную нити;
- Pn – параллельную нити.
Под действием силы Pt шарик будет стремиться вернуться в положение равновесия. Pt=P·sinj. При малых углах sinj @ j и тогда Pt=-m·g·j. Знак «-», т.к. сила Pt препятствует возрастанию угла j. Сила Pt не упругая сила, но по своему действию и характеру аналогична упругой силе. Такая сила называется квазиупругой силой.
Несмотря на большое разнообразие колебательных процессов, как по физической природе, так и по степени сложности, все они совершаются по некоторым общим закономерностям и могут быть сведены к совокупности простейших периодических колебаний, называемых гармоническими (от греческого “гармоникс” – стройный).
Дата добавления: 2016-11-04; просмотров: 2787;











