Описание установки и метода измерений

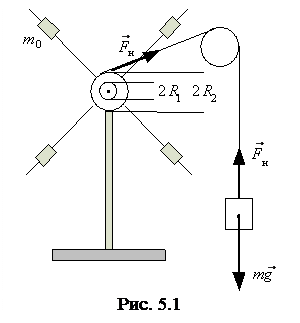Маятник Обербека, исполь-зуемый в данной работе, изображен на рис. 5.1. Он состоит из двух шкивов различного радиуса R₁ и R₂, укрепленных на одной горизонтальной оси (на рисунке отмечена точкой), и четырех стержней, на которые надеваются одинаковые передвижные грузы массой 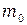.Грузы могут быть закреплены на разных расстояниях от оси вращения маятника. На один из шкивов навивается нить, которая перебрасывается через блок изменения направления движения нити. К свободному концу нити прикрепляется груз массой m, под действием которого маятник приводится во вращательное движение. Расстояние h, пройденное грузом за время t,отмечается по вертикальной шкале.

Основной закон динамики вращательного движения в данной работе удобно записать в виде

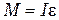, (5.1)

где M – вращающий момент, действующий на маятник, 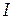– момент инерции маятника, 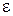– угловое ускорение маятника.

Для того чтобы убедиться в выполнении закона (5.1), в данной работе предлагается рассчитать момент инерции маятника теоретически и сравнить полученное значение с рассчитанным из опыта по формуле (5.1).

Теоретическое значение момента инерции маятника 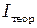рассчитывается как сумма моментов инерции составляющих его частей, т. е.

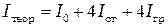, (5.2)

где 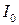– суммарный момент инерции двухступенчатого шкива и бобышки, на которой закреплены стержни, 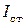– момент инерции одного стержня, 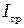– момент инерции подвижного груза.

Учитывая, что ось вращения стержней проходит через их концы, расположенные на оси вращения маятника (следовательно, 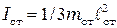), и считая подвижные грузы материальными точками (поскольку их размеры малы по сравнению с расстоянием до оси), можно (5.2) представить в виде

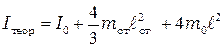, (5.3)

где 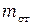– масса стержня, 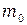– масса подвижного груза, 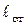– длина стержня, 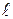– расстояние от центра масс грузов до оси вращения маятника.

Экспериментальное значение момента инерции маятника 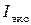находят с помощью формулы (5.1), из которой

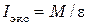. (5.4)

В данной работе силой трения в подшипниках можно пренебречь и считать, что вращение крестовины происходит под действием только момента силы натяжения нити 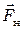. Которую легко найти, записав основной закон динамики (II закон Ньютона) для падающего груза (рис. 5.1) в векторном виде

,

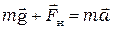затем – в скалярном виде 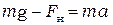. (5.5)

Из (5.5) следует, что 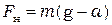, (5.6)

где g – ускорение свободного падения, 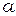– ускорение падения груза.

Груз падает равноускоренно, поэтому его ускорение 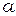можно найти, воспользовавшись уравнением равноускоренного движения

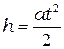, откуда 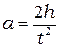. (5.7)

Подставив (5.7) в (5.6), получим

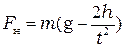. (5.8)

Из рис. 5.1 видно, что плечо силы натяжения равно радиусу шкива R, на который навита нить, следовательно,

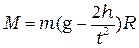. (5.9)

Для нахождения углового ускорения маятника можно считать, что нить нерастяжима, поэтому ускорение всех точек нити и любой точки обода шкива одинаково и равно ускорению груза. Это значит, что угловое ускорение крестовины можно найти по формуле

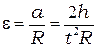, (5.10)

Подставив в формулу (5.4) выражения (5.9) и (5.10), получим формулу для расчета экспериментального значения момента инерции маятника

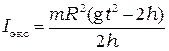. (5.11)