Описание установки и метода измерений

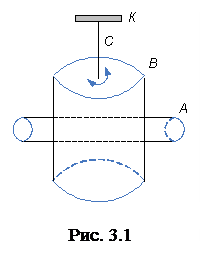
В настоящей работе для определения момента инерции тела, масса и размеры которого неизвестны (круглого стержня А), используют тело с известным моментом инерции (сплошной цилиндр В). Цилиндр, жёстко связанный с проволочным подвесом С, закреплен на штативе К (рис. 3.1). Если цилиндр вывести из положения равновесия, повернув его на небольшой угол 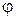, и предоставить самому себе, он будет совершать крутильные колебания. При деформации кручения в проволоке возникает возвращающий момент сил 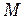, пропорциональный углу поворота

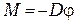, (3.1)

где D – модуль кручения проволоки. Знак ²–² говорит о том, что момент сил возвращает систему в положение равновесия.

Основной закон динамики вращательного движения 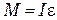для данного случая, с учетом (3.1), имеет вид

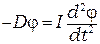, (3.2)

где 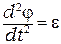– угловое ускорение тела.

Далее, введя обозначение 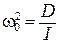, уравнению (3.2) можно придать вид

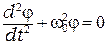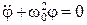, или . (3.3)

Уравнение (3.3) является однородным дифференциальным уравнением второго порядка. Из него следует, что угол поворота тела представляет собой следующую функцию времени:

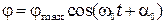, (3.4)

т. е. под действием момента силы, пропорционального углу поворота, тело совершает гармоническое колебательное движение.

Анализ уравнения (3.4) позволяет установить, что постоянные интегрирования 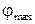и 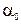представляют собой амплитуду и начальную фазу колебаний соответственно, а 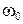– циклическую частоту, которая связана с периодом колебаний соотношением .

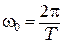Из последней формулы находим период крутильных колебаний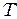

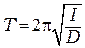. (3.5)

Если известен модуль кручения, то, используя формулу (3.5), можно найти момент инерции тела или системы тел, так как период колебаний легко определяется на опыте путем измерения времени 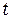, за которое тело совершает 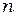колебаний

.

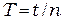В настоящей работе модуль кручения проволоки неизвестен, поэтому находят период колебаний цилиндра 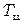и период колебаний системы ²цилиндр – стержень² 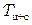по формулам:

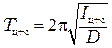, (3.6)

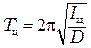, (3.7)

где 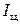– момент инерции цилиндра, 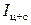– момент инерции системы ²цилиндр – стержень², равный сумме их моментов инерции .

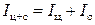Из совместного решения уравнений (3.6) и (3.7) следует, что

,

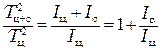откуда момент инерции стержня 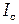равен

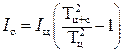. (3.8)

Момент инерции цилиндра относительно оси вращения, совпадающей с его осью симметрии, известен

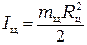. (3.9)

Подставив (3.9) в (3.8), получим окончательную формулу для расчёта экспериментального значения момента инерции стержня:

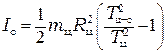. (3.10)

Теоретически момент инерции сплошного круглого стержня радиусом R_с относительно оси симметрии, перпендикулярной его длине, l_с, рассчитывается по формуле

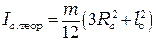. (3.11)