Уравнение неразрывности. Уравнение Бернулли.
Уравнение неразрывности.
Идеальная жидкость - это абстрактная жидкость, не обладающая вязкостью, теплопроводностью, способностью к электризации и намагничиванию.
Такое приближение допустимо для маловязкой жидкости. Течение жидкости называется стационарным, если вектор скорости в каждой точке пространства остается постоянным.
Графически движение жидкостей изображается с помощью линий тока.
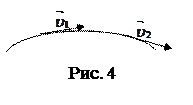 Линии тока жидкости - это линии, в каждой точке которых вектор скорости частиц жидкости направлен по касательной (рис. 4).
Линии тока жидкости - это линии, в каждой точке которых вектор скорости частиц жидкости направлен по касательной (рис. 4).
Линии тока проводят так, чтобы число линий, проведенных через некоторую единичную площадку, ^ потоку, было численно равно или пропорционально скорости жидкости в данном месте.
Часть жидкости, ограниченная линиями тока, называется трубкой тока.
Т.к. скорость частиц жидкости направлена по касательной к стенкам трубки тока, частицы жидкости не выходят из трубки тока, т.е. трубка - как жесткая конструкция. Трубки тока могут сужаться или расширяться в зависимости от скорости жидкости, хотя масса жидкости, протекающей через некоторое сечение, ^ ее течению, за определенный промежуток времени будет постоянной.
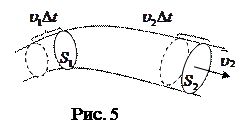 Т.к. жидкость несжимаема, через S1 и S2 пройдет за Dt одинаковая масса жидкости (рис. 5).
Т.к. жидкость несжимаема, через S1 и S2 пройдет за Dt одинаковая масса жидкости (рис. 5).
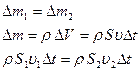
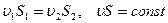 - уравнение неразрывности струи или теорема Эйлера.
- уравнение неразрывности струи или теорема Эйлера.
Произведение скорости течения несжимаемой жидкости и площади поперечного сечения одной и той же трубки тока постоянно.
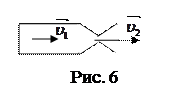 Теорема о неразрывности широко применяется при расчетах, связанных с подачей жидкого топлива в двигатели по трубам переменного сечения. Зависимость скорости потока от сечения канала, по которому течет жидкость или газ, используется при конструировании сопла ракетного двигателя. В месте сужения сопла (рис. 6) скорость истекающих из ракеты продуктов сгорания резко возрастает, а давление падает, благодаря чему возникает дополнительная сила тяги.
Теорема о неразрывности широко применяется при расчетах, связанных с подачей жидкого топлива в двигатели по трубам переменного сечения. Зависимость скорости потока от сечения канала, по которому течет жидкость или газ, используется при конструировании сопла ракетного двигателя. В месте сужения сопла (рис. 6) скорость истекающих из ракеты продуктов сгорания резко возрастает, а давление падает, благодаря чему возникает дополнительная сила тяги.
Уравнение Бернулли.
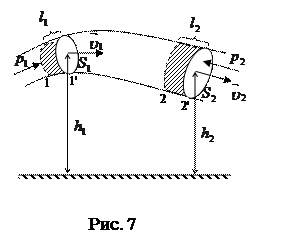 Пусть жидкость движется в поле сил тяжести так, что в данной точке пространства величина и направление скорости жидкости остаются постоянными. Такое течение называется стационарным. В стационарно текущей жидкости кроме сил тяжести действуют еще и силы давления. Выделим в стационарном потоке участок трубки тока, ограниченный сечениями S1 и S2 (рис.7)
Пусть жидкость движется в поле сил тяжести так, что в данной точке пространства величина и направление скорости жидкости остаются постоянными. Такое течение называется стационарным. В стационарно текущей жидкости кроме сил тяжести действуют еще и силы давления. Выделим в стационарном потоке участок трубки тока, ограниченный сечениями S1 и S2 (рис.7)
За время Dt этот объем переместится вдоль трубки тока, причем сечение S1 переместится в положение 1', пройдя путь 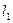 , а S2 - в положение 2', пройдя путь
, а S2 - в положение 2', пройдя путь 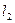 . В силу неразрывности струи выделенные объемы (и их массы) одинаковы:
. В силу неразрывности струи выделенные объемы (и их массы) одинаковы:
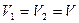 ,
, 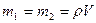 .
.
Энергия каждой частицы жидкости слагается из ее кинетической и потенциальной энергий в поле сил земного тяготения. Вследствие стационарности течения частица, находящаяся через Dt в любой из точек незаштрихованной части рассматриваемого объема, имеет такую же скорость, и, следовательно Wк, какую имела частица, находившаяся в той же точке в начальный момент времени. Поэтому изменение энергии всего рассматриваемого объема можно вычислить как разность энергий заштрихованных объемов V1 и V2.
Возьмем сечение трубки тока и отрезки 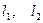 настолько малыми, чтобы всем точкам каждого из заштрихованных объемов можно было приписать одно и то же значение скорости, давления и высоты. Тогда приращение энергии равно:
настолько малыми, чтобы всем точкам каждого из заштрихованных объемов можно было приписать одно и то же значение скорости, давления и высоты. Тогда приращение энергии равно:
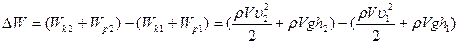
В идеальной жидкости трение отсутствует, поэтому DW должно равняться работе, совершенной над выделенным объемом силами давления:
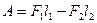
(«-» т.к. 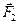 направлена в сторону, противоположную перемещению
направлена в сторону, противоположную перемещению 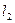 )
)
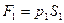 ,
, 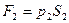 ,
,
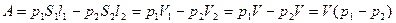 ,
,
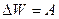 ,
,
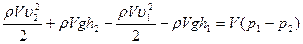 .
.
Сократим на V и перегруппируем члены:
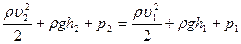 ,
,
сечения S1 и S2 были выбраны произвольно, поэтому можно утверждать, что в любом сечении трубки тока
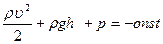 (1)
(1)
Выражение (1) представляет собой уравнение Бернулли. В стационарно текущей идеальной жидкости вдоль любой линии тока выполняется условие (1).
Для горизонтальной линии тока 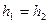 ,
, 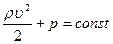
Уравнение Бернулли достаточно хорошо выполняется для реальных жидкостей, внутреннее трение в которых не очень велико.
Уменьшение давления в точках, где скорость потока больше, положено в основу устройства водоструйного насоса.
Выводы этого уравнения учитываются при расчетах конструкций насосов систем подачи жидкого топлива в двигатели.
Дата добавления: 2016-11-04; просмотров: 3419;











