Влияние радиуса и несовершенства скважины на ее

Производительность

Ранее были получены формулы для дебита скважины при установившемся режиме фильтрации жидкости, что позволяет нам установить влияние радиуса скважины r_C на ее дебит Q. Обратимся к плоскорадиальному потоку несжимаемой жидкости. По формуле Дюпюи зависимость дебита скважины Q от ее радиуса r_C и радиуса контура питания можно представить в виде

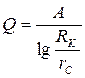, где А = const . (5.16)

Допустим, что при прочих неизменных условиях радиус скважины r_C увеличен в n раз, т.е. 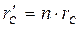, что определяет новый дебит 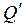по формуле (5.16). Тогда отношение дебитов представится следующим образом:

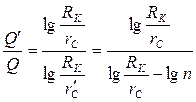. (5.17)

На основании формулы (5.16) построен график зависимости величины 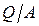от соотношения радиусов 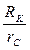, что при А = const и R_K = const , отражает зависимость дебита Q от радиуса r_C скважины (рис.33).

Из графика (рис.33) видно, что дебит скважины изменяется очень медленно в практически наиболее интересном диапазоне изменения отношения 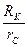от 10³ до 10⁶ (см. табл.1).

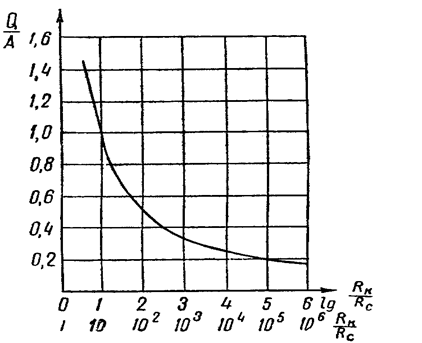
Рис. 33

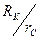
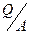
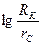
106 105 104 103 102	0.17 0.20 0.25 0.33 0.50 1.0

Табл.1.

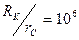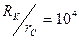На основании формулы (5.17) составлена табл.2 и построен график (рис.34) для случаев и , что соответствует 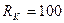км и 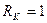км (соответственно) при .

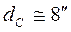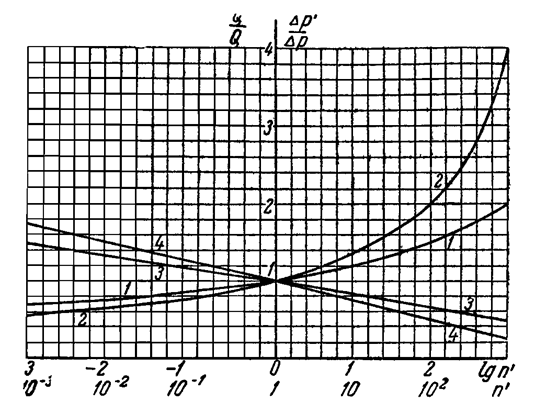
Рис. 34

n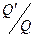
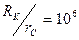
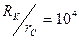
	1.0 1.05 1.2 1.5 2.0	1.0 1.08 1.33 2.0 4.0

Табл. 2

Из таблицы 2 (рис.34) видно, что изменение радиуса скважины сравнительно мало отражается на изменении ее дебита. Так, например, при 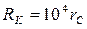, чтобы увеличить дебит вдвое, надо увеличить радиус скважины в 100 раз; наоборот – если увеличить радиус скважины вдвое, ее дебит увеличится только на 8 %. Если 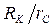еще больше ( 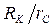= 10⁶ ), то величина радиуса еще меньше.

На рис.34 видно, что при n > 1 подъем кривых 1 и 2 интенсивнее, чем слева от той же оси, т.е. при n < 1 (уменьшение радиуса скважины). Следовательно, увеличение радиуса скважины в какое-то число n раз сильнее сказывается на дебите, чем уменьшение радиуса в это же n число раз. Так, например, при 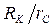= 10⁴ увеличение r_C в 10 раз вызывает увеличение дебита на 33%, а уменьшение радиуса r_C в 10 раз вызывает уменьшение дебита на 20%. Чем больше величина отношения 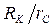и чем ближе n к 1, тем меньше разница между приростом и уменьшением дебита скважины при увеличении и уменьшении ее радиуса в одно и тоже n число раз.

Аналогичный анализ можно было бы провести и о влиянии радиуса скважины r_C на изменение перепада давления (Р_К – Р_С) при сохранении (Q = const) постоянного дебита. Такая зависимость 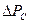от 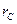показано на рис.34 (линии 3 и 4).

Формула анализа:

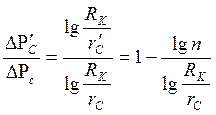. (5.18)

На основании формулы (5.18) можно утверждать, что 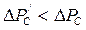при n>1, т.е. при увеличении радиуса скважины требуется создать меньшее понижение давления на забое для получения того же дебита, что и при первоначальном малом радиусе. Из прямолинейности линии 3 и 4 (рис.34) следует, что увеличение радиуса в некоторое число раз на столько уменьшает перепад давления в скважине, на сколько его увеличивает уменьшение радиуса в то же число раз.

Сопоставление результатов вычислений по формулам (5.17) и (5.18) показывает, что

Проведем анализ притока жидкости к гидродинамически несовершенной по степени вскрытия скважины. Для выяснения потери в дебите скважины от неполного вскрытия всей толщины пласта, интересно сравнить дебиты (5.2) – формула Маскета и (3.9) – формула Дюпюи через коэффициент совершенства скважины 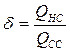. На рис. 35 приведены графики зависимости коэффициента совершенства скважины 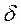от степени вскрытия пласта 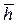(при этом R_K=10⁵r_c). На основании графиков (рис. 35) можно утверждать, что с увеличением степени вскрытия пласта коэффициент совершенства скважины, а, следовательно, и ее дебит возрастает сначала быстро, а затем все более медленно.

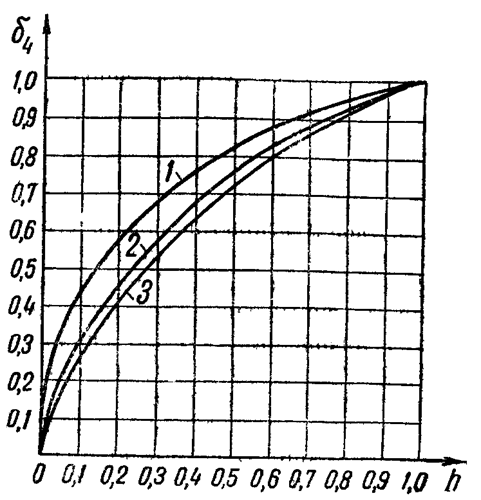
Рис. 35

Отмечается аналогичная закономерность при анализе влияния толщины пласта на дебит скважины: увеличение толщины пласта h первоначально активно влияет на дебит несовершенной скважины, имеющей постоянную глубину ее вскрытия; дальнейшее увеличение толщины пласта влияет менее интенсивно на величину дебита Q_HC несовершенной скважины.

Относительно влияния радиуса скважины r_c на величину дебита Q_HC можно заметить из формулы (5.2), что чем меньше степень вскрытия пласта скважиной 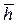, тем сильнее влияние радиуса r_c скважины на ее дебит.

Теперь проведем некоторый анализ притока жидкости к несовершенной по характеру вскрытия скважине.

Такой общий анализ влияния характера несовершенства скважины на ее дебит можно выполнить по кривым зависимости коэффициента фильтрационного сопротивления С₂ от параметров: 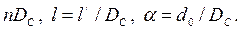Очевидна тенденция падения значения коэффициента С₂ при возрастании показателя nD₀ и a.

Исследователями отмечены основные важные моменты:

1) Положение интервала перфорации относительно кровли и подошвы пласта мало влияет на дебит скважины;

2) С ростом числа перфорационных отверстий до N=16¸20 на 1 п.м. толщины пласта дебит увеличивается; а при числе N>20 на 1 п.м. – дебит остается неизменным;

3) Сильное влияние на дебит оказывает длина перфорационного канала, с увеличением длины перфорационных каналов дебит увеличивается.