Учет несовершенства скважин при расчете их дебита по
Виды несовершенства скважин; расчетные формулы для дебита несовершенной скважины
Скважина называется гидродинамически совершенной, если она вскрывает продуктивный пласт на всю толщину и забой скважины открытый, т.е.вся вскрытая поверхность забоя является фильтрующей. Однако во многих случаях продуктивные пласты вскрываются скважинами не на всю их толщину, а частично; такие скважины считаются несовершенными.
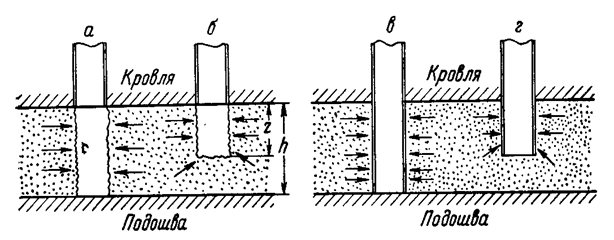
В подземной гидрогазодинамике различают два основных вида несовершенства скважины (рис. 28):
1) гидродинамически несовершенная по степени вскрытия продуктивного пласта;
2) гидродинамически несовершенная по характеру вскрытия пласта.
Скважина называется гидродинамически несовершенной по степени вскрытия пласта, если она вскрывает пласт не на всю толщину h пласта, а только на некоторую ее глубину b с открытым забоем; при этом отношение 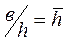 называется относительным вскрытием пласта.
называется относительным вскрытием пласта.
Скважина называется гидродинамически несовершенной по характеру вскрытия пласта, если она вскрывает весь пласт (до подошвы), но сообщение с пластом происходит через специальные отверстия в обсадной колонне и цементном камне или через специальные забойные фильтры.
 |
Нередко встречаются скважины с двойным видом несовершенства – как по степени, так и по характеру вскрытия пласта.
Рис.28. Схема гидродинамически совершенной и несовершенных скважин
А- гидродинамически совершенная скважина; б- скважина, не совершенная по степени вскрытия; в- скважина, не совершенная по характеру вскрытия; г- скважина, не совершенная по характеру и степени вскрытия.
Приток жидкости к несовершенным скважинам даже в горизонтальном однородном пласте постоянной толщины перестает быть плоскорадиальным. Строгое математическое решение задачи о притоке жидкости к несовершенной скважине в пластах конечной толщины представляет большие (иногда непреодолимые) математические трудности. Приведем без выводов и доказательств несколько известных решений по определению дебита несовершенной по степени вскрытия скважины.
Прежде всего допустим, что скважина вскрыла кровлю пласта неограниченной толщины (h ® ¥) и при этом ее забой имеет форму полусферы. В этом случае можно считать, что поток радиально-сферический при условии 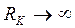 и тогда дебит определяется по формуле (4.7).
и тогда дебит определяется по формуле (4.7).
Если скважина вскрыла пласт неограниченной толщины на глубину b, то ее дебит можно найти по формуле Н.К. Гиринского:
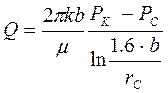 . (5.1)
. (5.1)
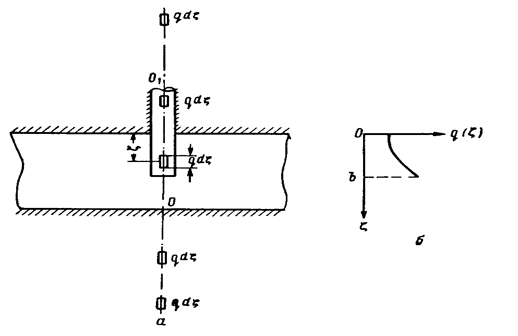 |
Задача о притоке жидкости к несовершенной по степени вскрытия пласта скважине в пласте конечной толщины h исследовалась М. Маскетом (1932г.). Вдоль оси скважины на вскрытой ее части длиной b он располагал воображаемую линию, поглощающую жидкость, каждый элемент которой
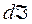 является стоком (рис. 29).
является стоком (рис. 29).
Рис. 29
Интенсивность расходов 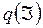 , т.е. дебитов, приходящихся на единицу длины поглощающей линии, подбиралась различной в разных ее точках для выполнения необходимых граничных условий:
, т.е. дебитов, приходящихся на единицу длины поглощающей линии, подбиралась различной в разных ее точках для выполнения необходимых граничных условий:
при r=RK, 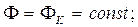
r=rC, 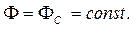
Выполнение условия непроницаемости кровли и подошвы пласта удовлетворялось отображением элементарных стоков 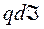 относительно кровли и подошвы пласта бесчисленное число раз.
относительно кровли и подошвы пласта бесчисленное число раз.
Подбирая интенсивность расходов q и используя метод суперпозиции действительных и отображенных стоков, М.Маскет получил следующую формулу для дебита гидродинамически несовершенной скважины:
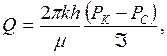 (5.2)
(5.2)
где 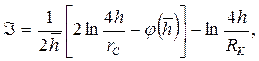
а функция 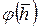 имеет следующее аналитическое выражение:
имеет следующее аналитическое выражение:
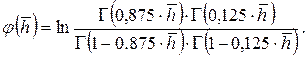 (5.3)
(5.3)
График функции 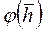 имеет вид (рис. 30).
имеет вид (рис. 30).
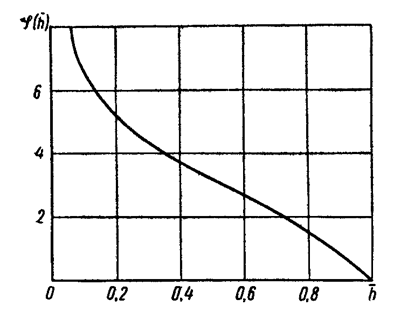 |
Рис. 30
Нетрудно заметить, что если 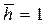 , т.е. пласт вскрыт на всю толщину, формула (5.2) переходит в формулу Дюпюи для плоскорадиального потока.
, т.е. пласт вскрыт на всю толщину, формула (5.2) переходит в формулу Дюпюи для плоскорадиального потока.
Иногда для расчета дебита несовершенной скважины используется более простая формула И. Козени
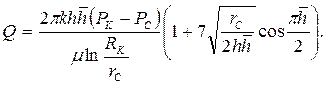 (5.4)
(5.4)
Отметим оригинальное упрощенное решение И.А. Чарного по определению дебита несовершенной по степени вскрытия скважины при малых значениях относительного вскрытия 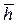 (b<<h). Область фильтрации условно разбивается на две зоны (рис. 31).
(b<<h). Область фильтрации условно разбивается на две зоны (рис. 31).
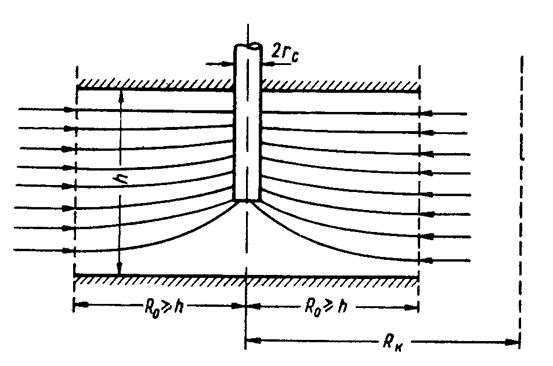
Рис. 31
Первая зона находится между контуром питания и радиусом R0 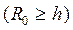 ; в этой зоне движение можно считать плоско-радиальным.
; в этой зоне движение можно считать плоско-радиальным.
Вторая зона расположена между стенкой скважины и цилиндрической поверхностью R0 , где движение будет пространственным.
Обозначим потенциал при r=R0 Ф=Ф0.
Тогда для зоны 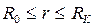 по формуле Дюпюи имеем:
по формуле Дюпюи имеем:
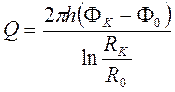 . (5.5)
. (5.5)
Для зоны 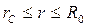 считаем движение радиально-сферическим между полусферами радиусами rc и R0; имеем:
считаем движение радиально-сферическим между полусферами радиусами rc и R0; имеем:
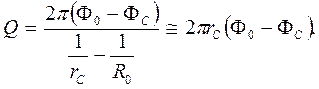 (5.6)
(5.6)
По идее «сращивания фильтрационных потоков» из формулы (5.5) и (5.6) по правилу производных пропорций получается формулы дебита скважины:
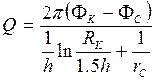 , здесь принято
, здесь принято 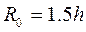 . (5.7)
. (5.7)
Приток жидкости и газа к совершенной по степени вскрытия скважине, но несовершенной по характеру вскрытия, рассматривался рядом авторов: М.Макетом (1943 г.), М.И.Тиховым (1947 г.) и А.Л.Хейном (1953 г.) и др. последняя и наиболее общая работа М.И.Тихова (1964) о притоке жидкости к полностью обсаженной и перфорированной скважине представляет (как и работы других авторов) скорее теоретический интерес и далека от ее практического инженерного приложения.
Еще большие трудности встречает строгое математическое решение задачи о притоке к несовершенной скважине и по степени и по характеру вскрытия пласта. Здесь следует отметить работы М.М. Глаговского (приближенное решение задачи о притоке жидкости к скважине, полностью обсаженной, но в различных интервалах перфорированной) и И.Чарного (скважина полностью обсажена, но перфорированная в верхней ее части).
Ряд сложных задач был решен В.И.Щуровым методом электрического моделирования, который заключается в следующем. Ванна заполняется электролитом. В электролит погружается один кольцевой электрод, моделирующий контур питания. В центре ванны помещается электрод на заданную глубину, соответствующую степени вскрытия пласта скважиной. К обоим электродам подводится разность потенциалов, являющаяся аналогом перепада давления. Сила тока является аналогом дебита скважины. Измеряя разность потенциалов и силу тока, по закону Ома можно подсчитать сопротивление, сделать перерасчет на фильтрационное сопротивление и определить дополнительное фильтрационное сопротивление, обусловленное несовершенством скважины.
Учет несовершенства скважин при расчете их дебита по
Дата добавления: 2016-11-04; просмотров: 5296;











