ЭЛЕМЕНТЫ КВАНТОВОЙ СТАТИСТИКИ И ФИЗИКИ ТВЕРДОГО ТЕЛА.
КЛАССИЧЕСКАЯ И КВАНТОВЫЕ СТАТИСТИКИ.
В системах, состоящих из очень большого числа частиц (газы, потоки света, электронное облако в металлах), невозможно проследить за движением одной частицы, тем более с учетом двойственной корпускулярно-волновой природы всех частиц. В таких случаях применяют статистические методы, вводя средние значения характеристик частиц и параметры, которые свойственны не отдельным частицам, а ансамблю частиц в целом.
В любой статистике основным законом является вероятностный закон распределения частиц по энергиям. Если обозначить энергию частицы как E, а
вероятность того, что частица имеет такую энергию как f, то должна быть известна функция распределения, т.е. зависимость f (E). Зная эту зависимость, можно найти число частиц с энергиями в заданном интервале и вычислить, например, теплоемкость, электрическую проводимость и др. свойства вещества.
В нашем курсе мы не можем рассматривать вывод функций распределения, укажем только, что существует классическая статистика Максвелла-Больцмана и две квантовые статистики
В классической статистике частицы считаются различимыми друг от друга В квантовой механике считается, что однотипные частицы, например, электроны, имеют совершенно одинаковые свойства – массу, электрический заряд, спин и считаются неразличимыми. Одни квантовые частицы имеют целые спины - их называют бозонами, поведение бозонов описывается симметричными пси-функциями, а статистику называют статистикой Бозе-Эйнштейна. Другие квантовые частицы имеют полуцелые спины, их называют фермионами, поведение их описывается антисимметричными пси-функциями, а статистика называется статистикой Ферми-Дирака. Фермионы подчиняются принципу Паули, а бозоны – нет.
1) Классическая статистика Максвелла – Больцмана. Она применяется в молекулярно-кинетической теории к молекулам газа. Закон распределения молекул по энергиям (закон Больцмана) имеет вид:
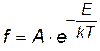
| f - вероятность того, что частица имеет энергию E, k – постоянная Больцмана, T – абсолютная температура | 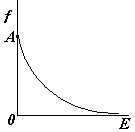
|
| График f (E) приведен на рис. А – некоторая константа (А = f при E = 0). Из графика и формулы следует, что классическая частица может иметь любую энергию, хотя и с разной вероятностью. |
2) Квантовая статистика Бозе – Эйнштейна. Описывает поведение бозонов - частиц с целым или нулевым спином. Например, атом водорода состоит из электрона и протона, имеющих полуцелые спины. Но спины могут быть либо параллельными, либо антипараллельными, поэтому атом водорода в нормальном состоянии будет бозоном. Ядро атома гелия-4 (альфа-частица) – тоже бозон, т.к. состоит из 2-х протонов и 2-х нейтронов. Сам атом гелия-4 тоже бозон, т.к. у него два электрона. Но ядро атома гелия-3, состоящее из двух протонов и одного нейтрона не является бозоном. К бозонам относятся также фотоны и мезоны.

| распределение Бозе-Эйнштейна; f - вероятность того, что частица имеет энергию E, k – постоянная Больцмана, T – абсолютная температура, m - некоторый параметр распределения. |
Бозоны не подчиняются принципу Паули, т.е. данное значение энергии могут иметь многие бозоны в системе.
Сверхтекучесть.
В 1938 г П.Л.Капица открыл явление сверхтекучести гелия. Гелий уникален тем, что даже при самых низких температурах он не затвердевает, оставаясь жидким.
В области температур от 4,2 К до 2,18 К (l - точка) гелий ведет себя как обычная жидкость, и в этой области температур его называют гелий-I. Ниже l - точки гелий становится сверхтекучим, и его называют гелий II.
Одно из свойств сверхтекучего гелия является способность проводить тепло без каких-либо потерь. Если подвести тепло к какой-либо точке жидкого гелия при температуре выше l - точки, жидкость закипит, бурно выделяя пузырьки. Если, продолжая подводить тепло к этой точке, охладить гелий до l - точки, кипение прекращается, потому, что тепло мгновенно распространяется по всему образцу, и вся жидкость сразу же приобретает одну и ту же температуру.
В сверхтекучем гелии отсутствует вязкость, он беспрепятственно протекает через самые узкие капилляры, которые не пропускают не только обычные жидкости, но и гелий-I.
При температурах ниже 1 К весь гелий переходит в сверхтекучее состояние.
Объяснить сверхтекучесть гелия можно только на квантовомеханическом уровне. Атом гелия имеет нулевой спин, т.е. является бозоном и, следовательно, не подчиняется принципу Паули. При понижении температуры энергия атома гелия понижается, и при достаточно низкой температуре все атомы оказываются в наинизшем возможном энергетическом состоянии. Но если все атомы имеют одну и ту же энергию, то они имеют и одну волновую функцию. Таким образом, атомы сверхтекучего гелия действуют согласованно, как единое целое. Поэтому когда мы прикладываем тепло в одной точке жидкого гелия, мы передаем ее сразу всему образцу. Между атомами невозможен обмен энергией, т.к.у всех она одна и та же – наинизшая. Энтропия сверхтекучего гелия равна нулю. Фермион только один может иметь данную энергию, или два, но с разнонаправленными спинами, поэтому гелий-3, является фермионом, не обладает сверхтекучестью.
Сверхпроводимость.
 В 1911 г. Камерлинг-Оннес обнаружил, что при температуре 7,2 К сопротивление свинца внезапно становится равным нулю.
В 1911 г. Камерлинг-Оннес обнаружил, что при температуре 7,2 К сопротивление свинца внезапно становится равным нулю.
(см. рис.), и свинец становится сверхпровдником. В одном из опытов в образце был наведен ток несколько сотен ампер, через год ток не изменился. В настоящее время известны более тысячи веществ, которые при различных низких температурах становятся сверхпроводниками. Очень важно, чтобы вещество было чистым, без посторонних примесей.
Квантовая теория сверхпроводимости был разработана Бардиным, Купером и Шриффером (теория БКШ). Как и сверхтекучесть, сверхпроводимость наблюдается для частиц, которые являются бозонами, т.е. имеющими нулевой или целый спин. В сверхпроводнике при некоторых условиях электроны проводимости объединяются попарно, при этом у них противоположно направлены спины, и они становятся бозонами. Эти пары неустойчивы, они легко разрушаются под действием тепловых колебаний, и могут существовать только при очень низких температурах. При некоторой критической температуре все пары-бозоны оказываются в наинизшем энергетическом состоянии и имеют одну и ту же волновую функцию. Ни одна из пар не может изменить своего состояния, т.к. у всех оно одно и то же. Поэтому при приложении внешнего поля попарные электроны действуют как единый коллектив, движутся все вместе, не теряя энергии и не встречая сопротивления.
Использование сверхпроводников в технике и для научных исследований имеют большие перспективы, т.к. при этом снижаются до минимума потери на джоулево тепло. Но пока они не получили широкого распространения из-за целого ряда трудностей. Например, создание поезда на магнитной подушке, который мог бы двигаться со скоростью 500 км/ч, требует огромных затрат, дорога должна быть прямой, неясно влияние сильных магнитных полей на пассажиров, содержание такой дороги стоит больше, чем содержание авиации. При передаче электроэнергии на большие расстояния выгоднее использовать переменный ток, тогда как сверхпроводники работают на постоянном токе. Многие трудности были бы преодолены, если бы удалось создать сверхпроводник
при более высоких температурах, в идеале – при комнатной температуре. Во всем мире идут поиски таких материалов, но пока максимальная температура 125 К.
3)Квантовая статистика Ферми-Дирака. Описывает поведение фермионов –частиц с полуцелым спином. К фермионам относятся электроны, протоны, нейтроны, нейтрино, ядра атома гелия-3. Мы будем рассматривать распределение Ферми-Дирака (ФД) только в применении к свободным электронам в металле. Основное отличие статистики ФД в том, что данное значение энергии может иметь только один электрон.
Закон распределения частиц по энергиям в статистике ФД имеет вид:
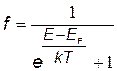
| распределение Ферми-Дирака, f - вероятность того, что частица имеет энергию E, k – постоянная Больцмана, T – абсолютная температура, EF – параметр распределения, называемый энергией или уровнем Ферми (см.дальше). |
На рисунках показаны графики функции ФД, их часто называют распределением электронов по энергиям. При температуре Т = 0 К вероятность того, что электрон имеет какое-либо значение энергии в пределах 0 ¸ EF равна единице; вероятность обнаружить электрон с энергией > EF равна нулю.
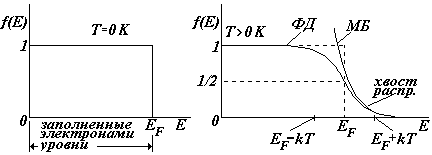
|
При температуре
Т > 0 К электроны за счет энергии теплового движения «покидают» свои уровни и переходят на более высокие.
Для металлов уровень Ферми (энергия Ферми) определяется следующим образом. (для полупроводников – см. дальше)
1)При Т = 0 К - это уровень энергии, отделяющий заполненные электронами
уровни от незаполненных или это максимальная энергия
электронов при Т = 0 К
2) При Т > 0 К - это энергетический уровень, который занимает электрон с
вероятностью, равной 1/2.
При высоких температурах или малых концентрациях электронов распределение ФД переходит в классическое распределение МБ. Действительно, при Е-ЕF >> кТ можно пренебречь единицей в знаменателе распределения ФД, тогда получим:

|
Иначе говоря, на хвосте распределения (см.рис.) можно использовать классическую формулу.
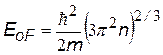
| Энергия Ферми при Т = 0 К, не зависит от числа электронов в образце и его объема, а определяется только концентрацией электронов n=N / V .Для одновалентных атомов характерны величины EoF @ 100 кТ @ 2,5 эВ | |
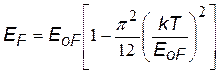
| Для металлов энергия Ферми очень слабо зависит от температуры (kT / EoF @ 0,01 при комнатных температурах) | |
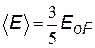
| средняя энергия электронов в зоне проводимости (см. дальше ) связана с энергией Ферми указанным образом |
Зная энергию Ферми EoF можно оценить скорость vF фермиевских электронов и их температуру ТF. Следует иметь в виду, что это не температура вещества, а температура воображаемого облака электронов, средняя скорость движения которых равна vF .
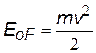 Þ vF
Þ vF
|  Þ ТF.
Þ ТF.
|
| элемент | EoF (эВ) | ТF., К | vF, 106 м/с |
| калий | 2,1 | 0,85 | |
| медь | 7,0 | 1,6 | |
| золото | 5,5 | 1,4 |
ЭЛЕМЕНТЫ ЗОННОЙ ТЕОРИИ ТВЕРДЫХ ТЕЛ.
Зонная теория – это один из разделов квантовой механики твердых тел – теория валентных электронов в периодическом поле кристаллической решетки.
Аналитически решить уравнение Шрёдингера для электрона, движущегося внутри металла, т.е. в поле, создаваемом множеством заряженных ионов решетки, невозможно. Для решения применяют различные приближенные методы.
Образование энергетических зон в кристаллах.
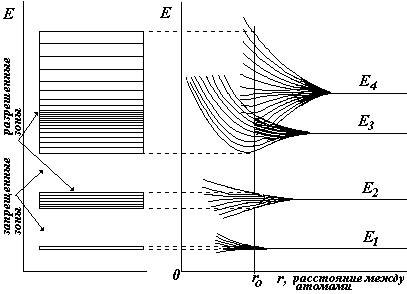 В отдельном атоме электрон имеет определенный набор энергий Е1, Е2 , Е3 ,.... Это проявляется в том, что спектры одноатомных газов линейчатые, т.е. состоят из отдельных линий. Чистый, без примесей металл состоит из однотипных атомов. При этом от каждого атома отрывается по одному, а у некоторых металлов по два электрона, ионы располагаются в строгом порядке, образуя кристаллическую решетку, а электроны свободно перемещаются внутри решетки, образуя облако электронного газа. Так как атомы однотипны, то у каждого электрона должен быть одинаковый набор энергий. Однако, в соответствии с принципом Паули электроны не могут иметь одинаковые энергии, поэтому в кристалле каждый энергетический уровень расщепляется на множество линий, лежащих вблизи исходного уровня, и образуются энергетические зоны. Не следует понимать эти зоны как некие пространственные области в металле, энергетические зоныэто интервалы значений энергий, которые «разрешено» иметь электронам (природой и квантовой механикой). Одни интервалы энергий называются разрешенными зонами, другие – запрещенными, т.е. такие энергии электроны иметь не могут.
В отдельном атоме электрон имеет определенный набор энергий Е1, Е2 , Е3 ,.... Это проявляется в том, что спектры одноатомных газов линейчатые, т.е. состоят из отдельных линий. Чистый, без примесей металл состоит из однотипных атомов. При этом от каждого атома отрывается по одному, а у некоторых металлов по два электрона, ионы располагаются в строгом порядке, образуя кристаллическую решетку, а электроны свободно перемещаются внутри решетки, образуя облако электронного газа. Так как атомы однотипны, то у каждого электрона должен быть одинаковый набор энергий. Однако, в соответствии с принципом Паули электроны не могут иметь одинаковые энергии, поэтому в кристалле каждый энергетический уровень расщепляется на множество линий, лежащих вблизи исходного уровня, и образуются энергетические зоны. Не следует понимать эти зоны как некие пространственные области в металле, энергетические зоныэто интервалы значений энергий, которые «разрешено» иметь электронам (природой и квантовой механикой). Одни интервалы энергий называются разрешенными зонами, другие – запрещенными, т.е. такие энергии электроны иметь не могут.
На рисунке показано символически , как можно представить себе образование зон. Здесь r – расстояние между атомами. При сближении атомов до некоторого расстояния r0 образуется кристалл, и, соответственно, энергетические зоны. В некоторых случаях зоны могут перекрываться, образуя более широкую зону. Чем дальше электрон от ядра, тем шире зона. Верхние зоны имеют ширину 1 эВ и более, нижние – несколько сотых эВ.
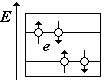 Каждый уровень должен расщепляется на N уровней, где N число свободных электронов в системе. Но данную энергию могут иметь 2 электрона с разнонаправленными спинами. Различие в направлениях спинов проявляется только при воздействии внешнего поля. Поэтому иногда говорят, что в зоне 2N уровней, а иногда N уровней, имея в виду, что на каждом уровне по 2 электрона с противоположно направленными спинами (см. рис.). В 1 см 3 Ме примерно 10 22- электронов. Если ширина зоны примерно 1 эВ, следовательно, расстояние между уровнями порядка 10 -22 эВ, поэтому говорят, что уровни в зоне распределены квазинепрерывно.
Каждый уровень должен расщепляется на N уровней, где N число свободных электронов в системе. Но данную энергию могут иметь 2 электрона с разнонаправленными спинами. Различие в направлениях спинов проявляется только при воздействии внешнего поля. Поэтому иногда говорят, что в зоне 2N уровней, а иногда N уровней, имея в виду, что на каждом уровне по 2 электрона с противоположно направленными спинами (см. рис.). В 1 см 3 Ме примерно 10 22- электронов. Если ширина зоны примерно 1 эВ, следовательно, расстояние между уровнями порядка 10 -22 эВ, поэтому говорят, что уровни в зоне распределены квазинепрерывно.
Уровни в зоне распределяются неравномерно, в середине зоны они располагаются гуще. Для характеристики распределения уровней пользуются понятием плотности уровней. Если на интервал энергий dE приходится dZ уровней, то
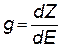 (1/эВ) (1/эВ)
| плотность энергетических уровней в зоне- по смыслу – это число уровней, приходящихся на единичный интервал энергий. | |
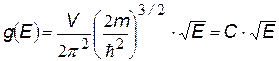
| Приближенная формула для зависимости плотности уровней от энергии; С = const для данного объема V тела, m- масса электрона | |
Проводники, полупроводники и диэлектрики.
Теоретически количество разрешенных зон бесконечно, а число электронов в данном теле хотя и очень велико, но имеет конечное значение. Поэтому не все зоны заполняются электронами. При температуре Т = 0 К заполнены полностью все зоны с наименьшей энергией, все остальные – пустые. Разрешенные зоны принято изображать прямоугольниками. Т.к. уровней в зоне огромное количество, целесообразно заполненную зону полностью или частично заштриховывать, а незаполненную - оставить пустой. Заполненная зона, граничащая с незаполненной, называется валентной, зона выше валентной называется зоной проводимости
Электрические свойства различных веществ - проводников (металлов), собственных полупроводников, диэлектриков и примесных полупроводников - с позиций зонной теории можно объяснить различной заполненностью зон электронами и шириной запрещенной зоны DЕ. И у металлов и у диэлектриков имеется множество свободных электронов, но у них разные энергетические возможности. Основное, что следует понять, что электрон только тогда «принимает», сообщаемую ему энергию, когда он при этом имеет возможность перейти на более высокий свободный энергетический уровень.
На рисунке показаны энергетические зоны для металла, собственного

|
полупроводника и диэлектрика.
Зоны, лежащие выше указанных, не заполнены электронами, нижележащие – полностью заполнены электронами (на рис.не показаны)
Металлы. У металлов зона проводимости частично заполнена электронами, там множество свободных уровней, энергетическое расстояние между которыми очень мало. Достаточно приложить к металлу небольшую разность потенциалов, и металл начинает проводить ток. Электроны «принимают» сообщаемую им энергию, в этой зоне у них большие энергетические возможности. Проводниками тока в металлах являются электроны.
Собственные полупроводники – это вещества, состоящие из однотипных атомов. Зонная схема представлена на среднем рисунке. За счет энергии теплового движения электроны переходят в зону проводимости, там множество свободных уровней, и электроны могут стать носителями тока. Одновременно в валентной зоне освобождается такое же количество «пустых мест».Обычно приводят сравнение со зрительным залом: с 1-го ряда человек ушел, на его место сел человек со 2-го ряд и т.д. Получается, что пустое место перемещается вглубь зала. «Пустое место» в валентной зоне называют дыркой. Дырка – это особое состояние электрона, которое ведет себя как положительный заряд +е.
Таким образом, проводимость собственных полупроводников одновременно и электронная и дырочная. У собственных полупроводников ширина запрещенной зоны DЕ невелика от сотых долей до 2 – 3 эВ. Например, у первых получивших широкое применение германия 1,1 эВ. у кремния 0,7 эВ.
Электропроводность полупроводников меньше, чем у металлов, но принципиальное их отличие в зависимости проводимости от температуры: с ростом температуры проводимость полупроводников увеличивается, а у металлов уменьшается (см.дальше). Энергия Ферми для полупроводников определяется как энергия, которую надо сообщить, чтобы увеличить число носителей тока на единицу (забросить 1 электрон из валентной зоны в зону проводимости). Для полупроводников уровень Ферми зависит от температуры в значительно большей степени, чем для металлов.
Диэлектрики(в электротехнике их называют изоляторами). Практически не проводят ток. В зонной теории это объясняется тем, что ширина запрещенной зоны DЕ велика, и электроны не могут попасть в зону проводимости. У типичного диэлектрика – алмаза DЕ @ 5 эВ. Реально, температура тела всегда > 0 К, поэтому некоторая доля электронов оказывается в валентной зоне, и любой диэлектрик обладает проводимостью, но эта проводимость ничтожно мала.
Примесные полупроводники. Если к собственному полупроводнику добавить небольшое количество чужеродных атомов (< 0,1 %) , то в зонной схеме собственного полупроводника появятся дополнительно зоны примеси. Эти зоны очень узкие, обычно говорят не зона, а примесные уровни. В зависимости от валентности примеси возможны два варианта:
 1) Примесные уровни заполнены электронами и располагаются ниже зоны проводимости вблизи ее дна (см. левый рис., здесь не соблюдены масштабы, ширина примесной зоны в тысячи раз уже зоны проводимости). За счет энергии теплового движения электроны с примесных уровней попадают в зону проводимости, где у них большие энергетические возможности, т.к.уровни свободны. Такие примеси называют донорными примесями(«поставщики электронов»), а сам полупроводник называют примесным полупроводником
1) Примесные уровни заполнены электронами и располагаются ниже зоны проводимости вблизи ее дна (см. левый рис., здесь не соблюдены масштабы, ширина примесной зоны в тысячи раз уже зоны проводимости). За счет энергии теплового движения электроны с примесных уровней попадают в зону проводимости, где у них большие энергетические возможности, т.к.уровни свободны. Такие примеси называют донорными примесями(«поставщики электронов»), а сам полупроводник называют примесным полупроводником
n - типа (часто говорят – донорный или электронныйполупроводник)
При переходе электронов в зону проводимости, в примесной зоне образуются дырки, но их энергия может меняться в очень узком интервале. Поэтому различают два типа носителей тока: основные носители – электроны и неосновные носители – дырки (подробнее см. дальше).
2) Примесные уровни пустые и располагаются вблизи валентной зоны (см.правый рисунок, все замечания относительно ширины зон справедливы и в этом случае).
Электроны из валентной зоны за счет энергии теплового движения переходят на свободные примесные уровни, здесь их энергия может меняться в очень узком интервале. В зону проводимости электроны могут попасть только при значительном повышении температуры, т.к. ширина запрещенной зоны
DЕ2 >> DЕ1. У дырок, образовавшихся в валентной зоне, большие энергетические возможности. Такие примеси называют акцепторными примесями, а полупроводник называют примесным полупроводником р - типа (часто говорят – акцепторный или дырочный полупроводник).
Донорными примесями становятся вещества с большей валентностью, а акцепторными – с меньшей, чем валентность основного собственного полупроводника. Например, для 4-х валентного германия донорными будут 5-ти валентные вещества, а 3-х валентные – акцепторными.
Дата добавления: 2021-02-19; просмотров: 587;











