Дифференциальные уравнения для элементов и систем
Вывод дифференциальных уравнений элементов системы – сложная творческая работа, при которой допускаются определенная идеализация процесса, пренебрежение отдельными факторами, рассмотрение частных случаев и т.д.
Математические описания элементов и систем осуществляются на основе физических, электрических, механических и др. законов, на которых основана работа элементов.
Учитывая сложность математического описания динамики процессов в элементах, часто прибегают к упрощенным уравнениям, с помощью которых получают приближенные решения исходной задачи.
Анализ линейных систем существенно проще, чем анализ нелинейных систем. Поэтому часто применяют линеаризацию нелинейных уравнений, то есть приведение нелинейных уравнений к линейным. Линеаризация основана на том, что в динамическом процессе автоматической системы все переменные изменяются так, что их отклонения от установившихся значений все время достаточно малы. Такое допущение справедливо, так как цель любой автоматической системы состоит в том, чтобы не допустить отклонений регулируемой величины (а значит, и всех параметров) от заданного значения. Основная идея метода линеаризации заключается в разложении исходного уравнения в ряд Тейлора в окрестности некоторой базовой точки, соответствующей заданному значению регулируемой величины, и вычитания из полученного уравнения в приращениях уравнения для установившего состояния. Таким образом, получают новое приближенное уравнение, которое отличается от исходного нелинейного тем, что входящие в него переменные заменены их малыми приращениями.
Геометрическая интерпретация метода линеаризации нелинейной функции xвых =f(xвх) представлена на рисунке 3.13.
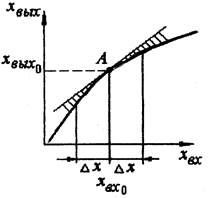
Рис 3.13. Линеаризация нелинейности.
Преобразование первоначальной нелинейной функции путем разложения в ряд Тейлора в окрестности точки А с координатами xвх 0 и xвых 0 и вычитания уравнения для установившегося режима равносильно замене исходной кривой на касательную, проведенную через точку установившегося режима.
При этом замена кривой на касательную всегда происходит с ошибкой (на рис. 3.13 заштрихована), величина которой увеличивается с увеличением отклонения аргумента от базового значения. Как видно, чем меньше ∆x, тем меньше ошибка линеаризации. С другой стороны возможность линеаризации тем шире, чем ближе линеаризуемая кривая к прямой.
При невозможности линеаризации пользуются методом решения нелинейных уравнений.
Наиболее сложной задачей является составление математического описания объекта регулирования (управления). Начинают описания с нахождения уравнений его материального или энергетического балансов (за бесконечно малый промежуток времени dt), выявления кинетических закономерностей, гидродинамических условий и т.п.
Составим математическое описание смесителя постоянного объема V, обеспечивающего идеальное перемешивание жидкости (рис. 3.14).
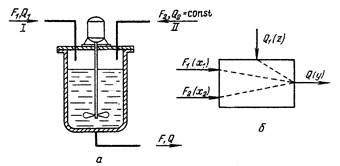
Рис 3.14. схемы смесителя двух жидкостей (а) и его динамических каналов (б).
В смеситель подаются жидкости, расходы и концентрации которых соответственно равны F1, Q1 и F2 , Q2. Выходной величиной смесителя является состав жидкости Q в смесителе и на выходе из него, а входными переменными – величины потоков на входе F1 и F2, а также концентрация Q1. Причем Q1 > Q >Q2.
Для нахождения уравнения динамики смесителя составим полный материальный баланс, а также материальный баланс с учетом концентрации вещества в каждом потоке за промежуток времени dt.
F1 + F2 =F, (3.14)
F1Q1 ·dt+ F2 Q2·dt =V·dQ+ FQ·dt, (3.15)
где F – расход жидкости на выходе из смесителя. Преобразуем уравнение (3.15) с учетом (3.14.)
| V∙ | dQ | +( F1 + F2) ·Q = F1·Q1+ F2·Q2 | (3.16) |
| dt |
Данное уравнение нелинейно, т. к. три его слагаемых представляют собой произведение переменных величин. Линеаризуем его, заменив каждую переменную на сумму базисного значения и приращения. Получим:
| V | d∆Q | + F10·Q+F10·∆Q0+Q0·∆F1+ F20·Q0+F20·∆Q+Q0·∆F2= | (3.17) |
| dt | |||
| =F10·Q10+F10·∆Q1+ Q10·∆F1+ F20·Q2+ Q2·∆F2 | |||
где базисные значения, обозначены теми же буквами, что и сами переменные, но с индексом нуль, и характеризуют равновесное состояние.
Уравнение смесителя при равновесном состоянии имеет вид
F10Q0+ F20·Q0=F10·Q10+ F20·Q2 (3.18)
Вычтем почленно уравнение (3.14) из уравнения (3.13), одновременно учитывая, что F10+F20= F0 , и найдем уравнение смесителя в приращениях
| V | d∆Q | + F0 ∆Q = F10·∆Q1+( Q10 - Q0 )·∆F1 - ( Q0 - Q2 ) ·∆F2. | . (3.19) |
| dt |
Из этого уравнения следует, что концентрация вещества Q в смесители возрастает с увеличением Q1 и F2, т.к. Q10 > Q0, и понижается с увеличением F2, т.к. Q0 > Q2 по условию.
Подставляя в уравнение (3.15.) относительные величины
| y= | ∆Q | ; z= | ∆Q1 | ; х1= | ∆F1 | ; х2= | ∆F2 | , |
| Q0 | Q10 | F10 | ∆F20 |
получим:
| VQ0 | dу | + F0Q0 у= F10·Q10 z+( Q10 −Q0 ) · F10· x1−(Q0 −Q2) · F20· x2 | . (3.20) |
| dt |
Разделив все слагаемые уравнения (3.20) на сомножители F0Q0, окончательно найдем
| Т0 | dу | + у =k1 · z +k2· х1 − k3· х2 | (3.21) |
| dt |
где Т0 = V/F0 – постоянная времени объекта; k1, k2 , k3, - коэффициент усиления по каналам Q1 − Q0 , F1 – Q , F2 – Q .
| к1= | F10 Q10 | , К2= | F10 (Q10 − Q0) | , К3= | F20 (Q0 − Q2) | . |
| F0 Q0 | F0 Q0 | F0 Q0 |
Таким образом, по всем трем каналам прохождения сигналов рассматриваемый смеситель представляет собой устойчивый объект 1-го порядка; его устойчивость объясняется наличием внутренней обратной связи.
Уравнение динамики смесителя в операторной форме будет:
(Т0 р +1) у = k1·z + k2·х1 − k3·х2 . (3.22)
Передаточная функция объекта по его каналам описывается равенствами:
| W1(p)= | к1 | , W2(p)= | К2 | , W3(p)= | К3 | . |
| (Т0р +1) | (Т0р +1) | (Т0р +1) |
Уравнению (3.22) соответствует структурная схема, приведенная на рис. 3.15.
Подробнее об операторной форме уравнения (3.22) и понятие передаточной функции будет рассмотрено в разделе 3.8.2.
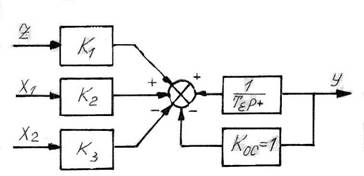
Рис. 3.15. Структурная схема смесителя двух жидкостей
В общем случае элементы и системы автоматического регулирования могут описываться линейными дифференциальными уравнениями с постоянными коэффициентами следующего вида:
| а0 | d n хвых | + a1 | d n-1 хвых | +…+an-1 | d хвых | + an ∙хвых = | |
| dtn | dt n-1 | dt | |||||
| =b0 | d m хвх | + b1 | d m-1 хвх | +…+bm-1 | d хвх | + bn ∙хвых | , (3.23) |
| dt m | dt m-1 | dt |
при этом в реальных системах n > m.
3.8.2. Передаточные функции
При исследовании АСР широко используются прикладные математические методы операционного исчисления, существенно облегчающие задачу исследования сложных систем регулирования. В частности, в теории автоматического регулирования используют преобразование функции вещественного переменного (времени) в функцию комплексного переменного, называемого преобразованием Лапласа.
Преобразованием функции-оригинала x(t) называется функция x(p) комплексного переменное p = a + j ω, определяемая интегралом Лапласа
∞
x(p) = ∫ x(t)∙ e-p∙ t dt . (3.24)
Символически преобразования Лапласа изображается следующим образом L[x(t)]= x (p).
Применение преобразования Лапласа превращает дифференциальные уравнения в алгебраические, что упрощает дальнейшее решение задач по описанию и расчету систем регулирования.
Для упрощения пользования преобразованием Лапласа составлены таблицы преобразований наиболее часто встречающихся функций и определены основные свойства преобразований Лапласа.
Применив преобразование Лапласа к дифференциальному уравнению (3.23) при нулевых начальных условиях (при t = 0, x (t) = 0, x'(t) = 0 и т.д.), получим уравнение, записанное в операторном виде,
(aор n + a1p n-1 + … + an-1p + an) xвых(p) =
= (b0p m + b1p m-1 + … + bm-1p + bm) xвх(p). (3.25)
На основе уравнения (3.25) получается выражение для передаточной функции:
| W (p)= | хвых(р) | = | b0p m + b1p m-1 + … + bm-1p + bm | = | В(р) | . (3.26) |
| хвх(р) | aор n + a1p n-1 + … + an-1p + an | А(р) |
Таким образом, передаточной функцией W(p) называется отношение преобразований Лапласа выходной величины к преобразованию Лапласа входной величины, найденных при нулевых начальных условиях.
Для быстрого определения W(p) по виду исходного дифференциального уравнения (3.23) существует формальное правило: необходимо предварительно заменить все производные на p в соответствующей степени, а затем разделить правую часть уравнения на левую. Например, d2 x/dt2 заменяют на p2, dx/dt на p, х на 1 и т.д.
3.8.3. Временные характеристики
Временной характеристикой, кривой разгона, называется зависимость изменения выходной величины во времени, полученная при ступенчатом изменении выходной величины. При единичном входном воздействии характеристика называется переходной, и в этом случае ее обозначают h(t). Из выражения (3.26) можно записать хвых(р) = W(р)·хвх(р). Учитывая, что преобразование Лапласа для единичного входного воздействия [хвх(t) = 1] будет L[1] = хвх(Р) = 1/Р, то переходная функция в операторном виде запишется так: хвых(Р) = W(Р)/Р.
Для обратного преобразования Лапласа в целях определения переходной функции можно воспользоваться формулой Хевисайда:
| h(t) = | + | n | ∙ е ркt | (3.27) | ||
| A(0) | ∑ | А(рк) | ||||
| B(0) | рк ∙ В' (рк) | |||||
| k=1 |
где рк – корни уравнения А(р) = 0.
3.8.4.Частотные характеристики
Если в выражении для передаточной функции вместо р поставить jω, то получим комплексную частотную характеристику W(jω), называемую амплитудно-фазовой частотной характеристикой (АФЧХ). Ее можно выразить через вещественную и мнимую составляющие, а также амплитудное и фазовое значение:
W(jω) = Р(ω) + j · Q(ω) = А(ω) · e jφ(ω) , (3.28)
где Р(ω) и Q(ω) – соответственно вещественная и минимальная составляющие АФЧХ; А(ω) – амплитудно-частотная характеристика (АЧХ), показывающая относительное изменение амплитуд выходного сигнала, по отношению к амплитуде входного сигнала от частоты ω входных колебаний; φ(ω) - фазочастотная характеристика (ФЧХ) , показывающая зависимость фазы выходных сигналов от частоты ω входных колебаний.
Частотные характеристики можно получить и экспериментально: если на вход системы подать гармоническое воздействие хвх с частотой ω и амплитудой Авх, то через определенное время на выходе также установятся гармонические колебания с частотой ω, но с амплитудой сигнала Авых и сдвинутые по фазе на φ(ω).
Графически годограф АФЧХ (3.38) представлен на рис.3.16.
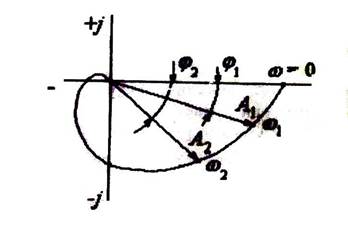
Рис.3.16. Амплитудно-фазовая частотная характеристика
3.8.5.Типовые динамические звенья АСР
Звенья АСР могут иметьразличные физические принципы действия,различные схемы и конструктивные формы, а также назначения. Однако с точки зрения динамических свойств звена, имеют значения лишь уравнения, связывающие выходную и входную величины звена. В классическом варианте выделяется обычно семь типовых звеньев: 1. Безинерционное звено;2.Инерционное звено; 3.Интегрирующее звено; 4.Дифференцирующее звено; 5.Колебательное звено; 6. Упругое (интегро-дифференцирующее) звено;7. Запаздывающее звено.
1.Безинерционное (статическое) звено. Оно называется также пропорциональным или усилительным звеном и описывается простейшим алгебраическим уравнением
хвых = К·хвх, (3.29)
где К – коэффициент передачи.
Выходная величина этого звена пропорциональна входной величине. Примеры такого звена показаны на рис 3.17. Из (3.29) имеем:
хвых (р) = К· хвх (р), (3.30)
и тогда передаточная функция будет:
| W(p) = | хвых (р) | = К . | (3.31) |
| хвх (р) |
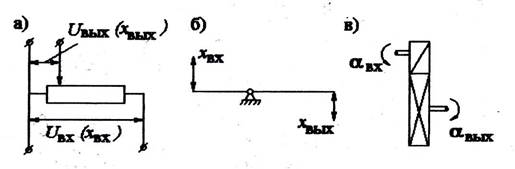
Рис. 3.17. Примеры безинерционного звена:
а- потенциометр; б –рычаг; в – редуктор.
Переходная функция звена получается из алгебраического уравнения при подаче на вход единичного воздействия.
h(t)=K. (3.32)

рис 3.18. характеристики безинерционного звена:
а - переходная функция; б – АФЧК; в – АЧХ; г – ФЧХ.
Как видно, АФЧХ представляет собой точку на действительной оси комплексной плоскости, АЧХ постоянна для всех значений частот, а фазовый сдвиг равен нулю φ(ω) = 0
2.Инерционное (апериодическое) звено. Описывается следующим дифференциальным уравнением первого порядка.
| Т | dxвых | +xвых = K∙ хвх | (3.33) |
| dt |
где Т – постоянная времени, К – коэффициент передачи.
Примеры систем, эквивалентных инерционному звену, представлены на рис 3.19.
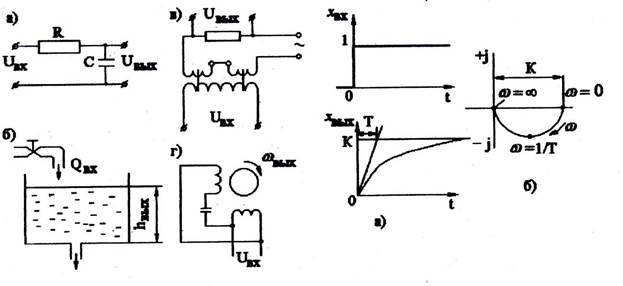
Рис.3.19. Примеры апериодического звена: Рис.3.20. Переходная функция (а)
а – RC-контур; б – одноемкостной гидра- и амплитудно-фазовая частотная
влический объект; в – магнитный усили- характеристика (б) апериодическо-
тель; г – двухфазный асинхронный двига- го звена.
тель.
Переходная функция инерционного звена представляет собой экспоненту с постоянной времени Т (рис. 3.20, а)
h(t) = K·(1-e-t/T) . (3.34)
Передаточная функция звена будет
| W(p)= | хвых (р) | = | К | (3.35) |
| хвх (р), | Тр + 1 |
Амплитудно-фазовая характеристика звена
| W(jω)=A(ω)·ejφ(ω ) = | K | ∙ e- j∙arc tg(Tω ) . (3.36) |
| √ 1 + (Т ω)2 |
Итак, рассмотрев различные системы, относящиеся к двум типовым динамическим звеньям, мы показали, что они могут описываться общими уравнениями, устанавливающими связь между выходными и входными величинами. Ограниченность объема учебного пособия не позволяет рассмотреть подробно остальные типовые динамические звенья. Приведем лишь некоторые их характеристики (Табл 3.1) [47].
Таблица 3.1.
3.8.6. Основные виды соединений звеньев системы
Различные сложные соединения звеньев основываются, в основном, на трех типовых соединениях: последовательном, параллельном встречно-параллельном (соединение с обратной связью). Рассмотрим их основные уравнения.
Последовательное соединениезвеньев (рис.3.21). Передаточнаяфункция «n» последовательно соединенных звеньев, равна произведению передаточных функций этих звеньев.
n
| WЭ(р) = | хвых.. п (р) | =W1(p)∙ W2(p) …Wп(р) = ∏ Wi(p) . (3.37) |
| хвх (р) |
i=1
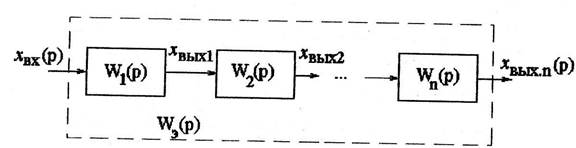
Рис.3.21. Схема последовательного соединения звеньев.
Параллельное соединение звеньев (рис.3.22).
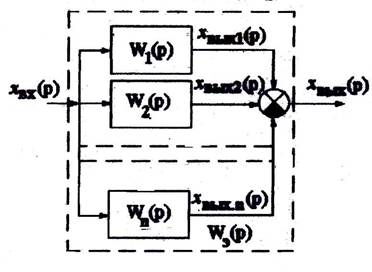
Рис.3.22. Схема параллельного соединения
Передаточная функция параллельного соединения звеньев Wэ(р) равна сумме передаточных функций этих звеньев:
| Wэ(р) = | n | Wi(p). | (3.38) |
| ∑ | |||
| i=1 |
Соединение с обратной связью (рис.3.23) характеризуется наличием цепи передачи выходного сигнала на вход системы. Обратная связь является основой работы замкнутых систем, действующих по отклонению регулируемой величины. В системах автоматического регулирования бывает обратная связь основная, как правило отрицательная, и дополнительные обратные связи, предназначенные для коррекции динамических характеристик отдельных звеньев. Последние могут быть как отрицательными, так и положительными.
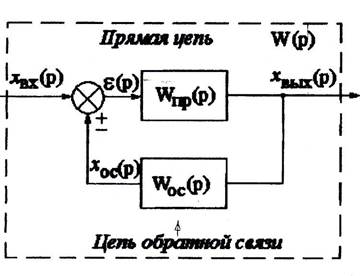
Рис. 3.23. Схема системы с обратной связью
Как видно, выходной сигнал прямой цепи, он же выходной сигнал системы хвых(р), через цепь обратной связи в виде хос(р) подается на выход системы. Результат рассогласования ε(р) входного сигнала и сигнала обратной связи подается на выход системы. На основании несложных рассуждений с учетом вышеприведенных правил для последовательного и параллельного соединения звеньев получаем выражение для передаточной функции замкнутой системы:
| W(p) = | хвых(р) | = | Wпр(р) | , (3.39) |
| хвх(р) | 1± Wпр(р)∙Wос(р) |
где знаки (+) и (-) соответствуют отрицательной и положительной обратной связи.
На основе приведенных трех типов соединений звеньев создаются более сложные структурные схема реальных АСР.
3.8.7.Устойчивость одноконтурных АСР
Понятия об устойчивости.Одним из важных и необходимых условий работоспособности АСР является их устойчивость. АСР находится в состоянии равновесия, если регулируемая величина не изменяется во времени.
Процесс регулирования устойчив, если после отклонения АСР от положения равновесия и устранения возмущения, вызвавшего это отклонение, она вновь с течением времени возвращается к исходному состоянию.
Различаются три вида состояний равновесия: 1) устойчивое; 2) безразличное; 3) неустойчивое. Эти виды равновесия схематически иллюстрируются на рис.3.24. с помощью различного расположения шариков.
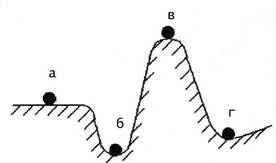
Рис.3.24. Схема, иллюстрирующая виды равновесия:
а – безразличное равновесие;
б и г – устойчивое равновесие; в – неустойчивое равновесие.
Математически задача устойчивости была решена А.М.Ляпуновым. Так как это решение справедливо для малых отклонений, то при исследовании исходят из линеаризованных дифференциальных уравнений. В соответствии с вышеприведенным определением устойчивости системы ее поведение характеризуется свободным движением. Решение дифференциального уравнения системы состоит из свободной и вынужденной составляющих. Вынужденная составляющая движения определяется возмущающими воздействиями и свойствами самой системы. Свободная же составляющая движения определяется только свойствами самой системы и по характеру свободного движения можно судить об основных динамических показателях системы.
Поэтому при исследовании устойчивости систем анализируют свободную составляющую решения, которая аналитически получается из однородного дифференциального уравнения (с нулевой правой частью):
| а0 | d n хвых | + a1 | d n-1 хвых | +…+an-1 | d хвых | + an ∙хвых = 0 | . (3.40) |
| dt n | dt n-1 | dt |
Решение уравнения (3.40) записывается так:
| xвых (t) = | n | Ck ∙ e pк∙ t | (3.41) |
| ∑ | |||
| к=1 |
где Ск –постоянная интегрирования; рк – корни характеристического уравнения исходного дифференциального уравнения.
Характеристическое уравнение имеет вид:
a0 рn + a1 pn-1 + … + an-1 p + an = 0 (3.42)
и совпадает со знаменателем передаточной функции W(p) = B(p)/A(p), поэтому может быть определено из W(р), приравниванием к нулю ее знаменателя А(р) = 0.
Система автоматического регулирования будет устойчива, если с течением времени все составляющие решения (3.41) стремятся к нулю. Корни характеристического уравнения (3.42) могут быть вещественными (в т.ч. и нулевые), комплексными и мнимыми:
рк = αк ; рк = βк ±jωк; рк = ± jωк.
Графики решений (3.41) имеют вид, представленный на рис. 3.25.
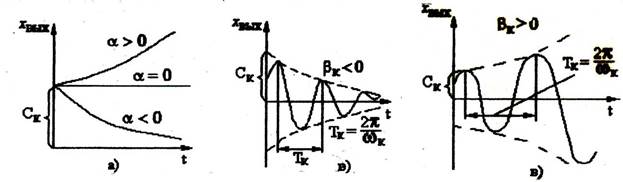
Рис.3.25. Переходные процессы для различных видов корней характеристического уравнения системы: а- вещественные корни, б,в – комплексные.
Как видно из графиков (рис.3.25) решений, переходные процессы при отрицательной вещественной части комплексных корней – имеют вид затухающих колебаний, а при мнимых корнях имеем незатухающие колебания.
Таким образом, для устойчивой линейной системы автоматического регулирования необходимо и достаточно, чтобы вещественные части всех корней характеристического уравнения были отрицательными.
Однако сложность вычисления корней характеристического уравнения АСР (в период до появления современных средств вычислительной техники) вызвала необходимость косвенных методов оценки устойчивости систем, названных критериями устойчивости.
Критерии устойчивости. Существует ряд алгебраических критериев устойчивости (Гурвица, Раусса, Вышеградтского И.А.), основанных на определенных соотношениях коэффициентов характеристического уравнения. Уровень сложности этих критериев зависит от порядка характеристического уравнения.
На практике часто отдают предпочтение частотным критериям устойчивости (в частности критерию Найквиста).
Частотный критерий устойчивости Найквиста (рис. 3.26). Этот критерий получил широкое применение в практике расчетов систем автоматизации благодаря ряду достоинств:
-для анализа устойчивости системы по этому критерию используется амплитудно-фазовая частотная характеристика разомкнутой системы, которая может быть получена как аналитическим, так и экспериментальным путем, что особенно важно;
-использование АФЧХ разомкнутой системы позволяет без риска для АСР, которая может оказаться неустойчивой в замкнутом состоянии, оценить ее устойчивость в замкнутом состоянии до аппаратурного замыкания.

Рис. 3.26. К определению устойчивости системы
по критерию Найквиста
Основная формулировка критерия Найквиста сводится к следующему: АСР, устойчивая в разомкнутом состоянии, будет устойчива и в замкнутом состоянии, если амплитудно-фазовая частотная характеристика разомкнутой системы не охватывает точку с координатами (-1; j0).
3.8.8. Качество АСР
Показатели качества. Условие устойчивости АСР является необходимым, но недостаточным для практического применения системы, ибо переходный процесс в системах может быть слишком медленным, либо слишком колебательным, либо отличаться недопустимыми отклонениями регулируемой величины. Поэтому система должна отвечать определенным показателям качества регулирования. Оценка качества АСР осуществляется по характеру переходного процесса в системе, получаемого при воздействии на него наиболее типичных возмущений. Чаще всего в качестве типового возмущающего воздействия используют ступенчатое входное воздействие, характеризующее наиболее тяжелый режим работы оборудования. Это может быть режим пуска, останова, сброса нагрузки и т.д.
хвх(t) = 0 при t > 0,
хвх(t) = а при t < 0, где а – константа.
На рис.3.27 приведены переходные процессы при обработке по управляющему (рис.3.27,а) и возмущающему (рис.3.27,б) воздействиям.
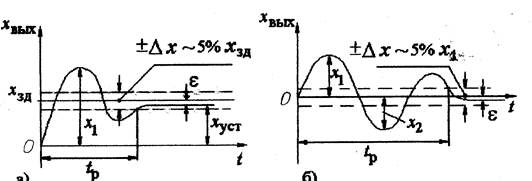
Рис.3.27. Показатели качества переходного процесса.
Основными показателями качества процесса регулирования являются следующие.
Перерегулированиеσ характерезует максимальное динамическое отклонение регулируемой величины х1 от исходного состояния равновесия. При этом для переходного процесса по управляющему воздействию (по заданию хзд), показанному на рис.3.27,а, перерегулирование выражается в % от установившегося значения регулируемой величины:
σ = [(х1 – х уст ) / х уст] · 100. (3.43)
При регулировании по возмущающему воздействию перерегулирование определяется по отношениям двух соседних амплитуд колебаний (рис.3.27,б):
σ= ( |х2| /х1)·100. (3.44)
Время регулирования tр- это промежуток времени от момента нанесения воздействия и соответствующего отклонения регулируемой величины до момента возвращения ее регулятором к исходному значению с точностью ±5% величины максимального динамического отклонения регулируемой величины х1 (при регулировании по возмущению) или до момента достижения регулируемой величиной нового заданного значения с точностью ± 5% (при регулировании по управляющему воздействию).
Остаточное отклонение ε – отклонение регулируемой величины в новом установившемся режиме от заданного значения при регулировании по управляющему воздействию, т.е.ε = хзд – хуст, а при регулировании по возмущающему воздействию ε характеризует отклонение регулируемой величины от исходного при окончании процесса регулирования (3.27,б).
Итак, остаточное отклонение характеризует статическую точность системы регулирования.
Перерегулирование и время регулирования являются основными показателями качества и тесно взаимосвязаны. Действительно, перерегулирование связано со скоростью, с которой регулируемая величина подходит к установившемуся значению, и чем выше эта скорость, тем больше перерегулирование и колебательность переходного процесса .
При уменьшении этой скорости в целях в целях уменьшения перерегулирования , т.е. улучшения динамической точности, происходит увеличение времени регулирования, что также нежелательно. Поэтому принимают компромиссное решение, допуская некоторое перерегулирование, например, в 20…45% , при котором обычно получается переходный процесс с 2 ÷ 3 колебаниями.
Итак, все показатели сводятся к двум основным показателям: статической и динамической точности регулирования.
Для уменьшения величины статической ошибки, а следовательно повышения точности регулирования, необходимо увеличить коэффициент усиления системы. Однако увеличение коэффициента усиления системы ведет к снижению запаса устойчивости. Это видно, например, из критерия устойчивости Найквиста, т. к. увеличение коэффициента усиления системы увеличивается модуль А(ω) амплитудно-фазовой характеристики, приближая его к критической точке [-1, j0],снижая тем самым запас устойчивости системы.
Поэтому приходится идти на компромисс, допуска определенную величину статической ошибки регулирования, при которой обеспечивается необходимый запас устойчивости системы.
Методы оценки качества переходного процесса. Анализ качества АСР наиболее полно можно осуществить, построив переходный процесс. Существует ряд методов построения переходного процесса, которые отличаются друг от друга степенью трудоемкости и точности. В инженерной практике чаще пользуются приближенными методами оценки качества переходных процессов на основе либо графика вещественной частотной характеристики замкнутой системы, либо расположения корней характеристического уравнения системы на комплексной плоскости корней.
Частотный метод оценки качества. Метод позволяет установить ряд текущих зависимостей, дающих возможность оценить качество переходного процесса без его построения, но на основе анализа вещественной частотной характеристики Р(ω) замкнутой системы, связанной интегральным соотношением с переходным процессом h(t):
∞
| h(t)= | ∫ | H( ω ) | ∙sin ωt ∙d ω | (3.45) | |
| π | ω |
При определенных затруднениях непосредственного вычисления интеграла (3.45), прибегают к графическому вычислению указанных интегралов. Для этого вещественную частотную характеристику разбивают на типовые трапециидальные или треугольные характеристики, для которых переходные
n
процессы табулированы (hį (t)), а далее находят h(t)= ∑hį (t).
i=1
Многоконтурные АСР
Удовлетворительное качество регулирования в простейшей одноконтурной системе с использованием стандартных типовых законов можно обеспечить лишь при благоприятных динамических характеристиках объекта. Большинство же промышленных объектов химической технологии характеризуется значительным чистым запаздыванием и большими постоянными времени. В этих случаях даже при оптимальных настройках регуляторов одноконтурные АСР характеризуются большими динамическими ошибками, низкой частотой регулирования и длительными переходными процессами. Для повышения качества регулирования необходим переход от одноконтурных АСР к более сложным системам, использующим дополнительные (корректирующие) импульсы по возмущениям или вспомогательным выходным координатам. Такие системы кроме обычного стандартного регулятора содержат вспомогательные регулирующие устройства – динамические компенсаторы или дополнительные регуляторы.
По характеру корректирующего импульса различают следующие многоконтурные АСР: комбинированные, сочетающие обычный замкнутый контур регулирования с дополнительным каналом воздействия, по которому через динамический компенсатор вводится импульс по возмущению; каскадные – двухконтурные замкнутые АСР, построенные на базе двух стандартных регуляторов и использующие для регулирования кроме основной выходной координаты дополнительный промежуточный выход; с дополнительным импульсом по производной от промежуточной выходной координаты.
Дата добавления: 2021-02-19; просмотров: 642;











