Примеры задаются формулами.
3) X – это дискретная случайная величина, t – это непрерывный параметр.
Этот класс на графике изображается так:
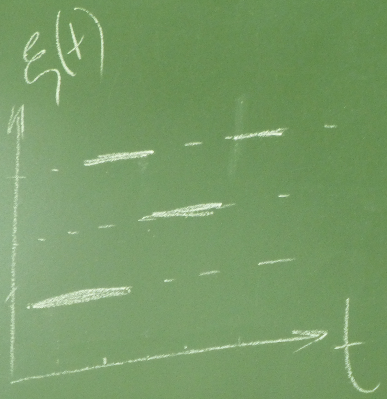
Пример:
Время непрерывно (идёт какими-то отрезками), а случайная величина меняется.
В промежутке времени от 10-и до 11-и часов дня будет разное количество людей (т.е. в одно и тоже время будет разное количество людей), назовём где: магазин, метро, троллейбус и т.п.
4) X – это дискретная случайная величина, t – это дискретный параметр.
Этот класс на графике изображается так:
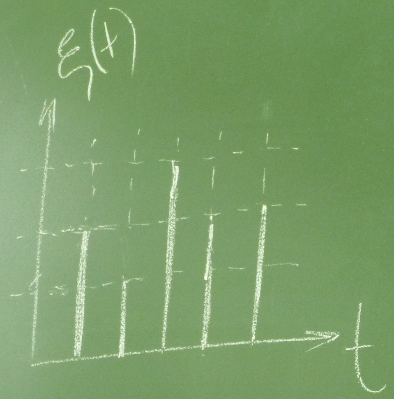
Т.е. 2 графика накладываются друг на друга:
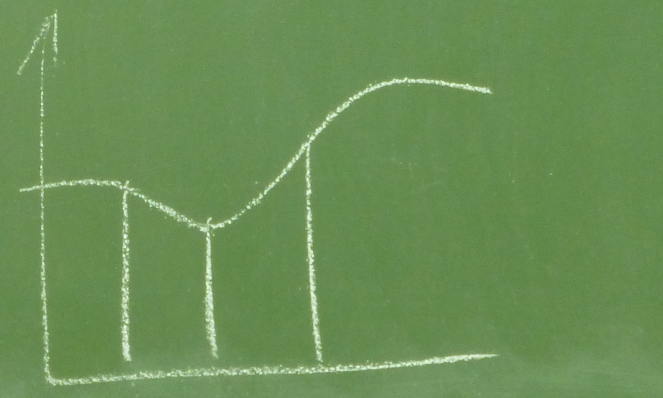
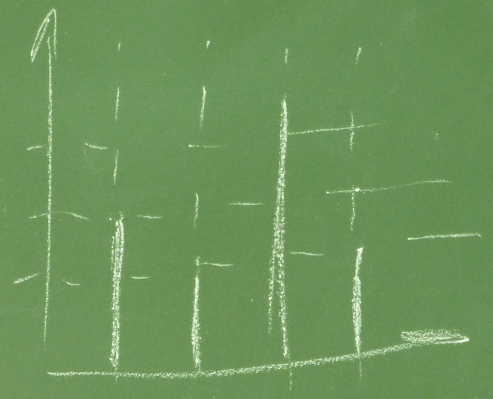
В определённый момент времени происходит какое-то множество случайных величин (они описываются функциями).
Пример: оцифрованный звук.
Случайный процесс – это случайная функция времени. Это означает, что наблюдатель видит только одну реализацию случайного процесса из множества возможных функций.
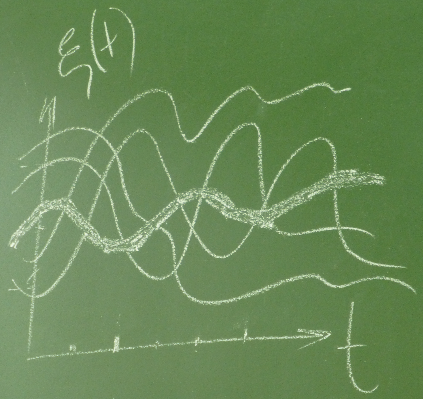
Ансамбль – это полный набор всех возможных реализаций.
Случайный процесс – это и есть ансамбль реализаций, а не функция в обычном её понимании.
Характеристикой случайного процесса в каждый фиксированный момент времени (t=t1) является плотность распределения вероятности P(X) случайной величины X(t).
По этим данным можно найти среднее значение, математическое ожидание, дисперсию, среднеквадратическое отклонение и другие характеристики случайного процесса.
Центрированные процессы – это процессы с нулевым средним значением.
Решим задачу:
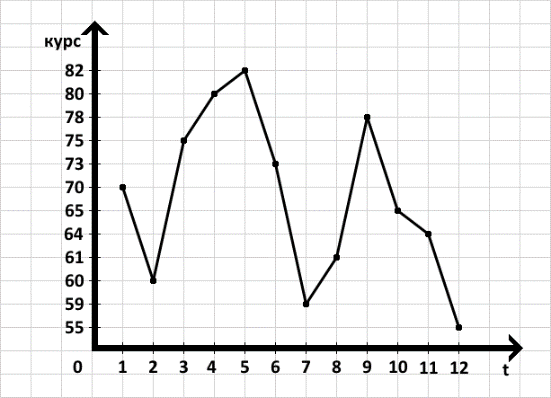
Выберем для примера какой-нибудь экономический случайный процесс, связанный с цифрами (меняющиеся во времени, скажем, каждый час). Выберем в качестве примера курс валюты.
Случайная величина – это у нас курс валюты.
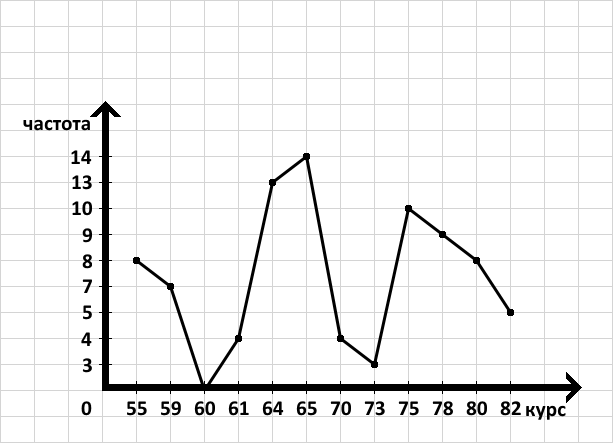
Частота – это у нас сколько дней встречался курс валюты.

И к этому всему ещё добавится вероятность.
Мы должны:
1) построить таблицу, состоящую из: X, 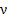 , P.
, P.
2) распределить значения случайных величин по возрастанию (ещё для удобства мы изменим таблицу)
3) построить график случайных величин (по возрастанию) по частоте возникновения
4) построить график случайных величин (по возрастанию) по месяцам
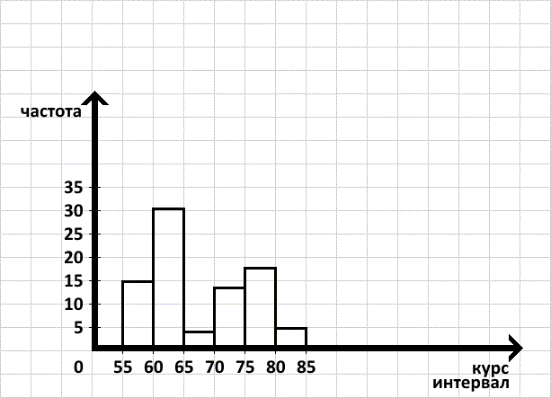
5) построить график – гистограмму распределения случайных величин (для этого надо разбить от 55 до 82-х на определённое количество интервалов, а также записать сумму появления этих чисел)
Решение:
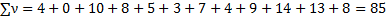

X: 55, 59, 60, 61, 64, 65, 70, 73, 75, 78, 80, 82

Найдём среднее значение:
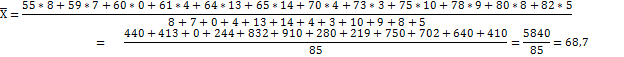
| Интервал | 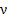
|
| 55 – 60 | |
| 61 – 65 | |
| 66 – 70 | |
| 71 – 75 | |
| 76 – 80 | |
| 81 – 85 | |
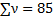
|
(т.е. мы складываем частоту тех случайных величин, которые входят в интервал, пример: интервал 55 – 60 (частоты случайных величин: 8(55), 7(59), 0(60)), частота = 8+7+0=15)
Дата добавления: 2016-11-04; просмотров: 876;











