Отображения и функции
Определение 2.1. Рассмотрим два непустых множества X и Y. Если каждому элементу множества X соответствует один элемент множества Y, то говорят, что задано отображение f множества X в множество Y.
Этот факт обычно записывают в виде:
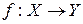 .
.
Определение 2.2. Элемент из множества Y, соответствующий элементу 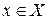 , обозначают
, обозначают 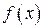 и называют образом элемента x относительно отображения f. При этом элемент x называется прообразом элемента
и называют образом элемента x относительно отображения f. При этом элемент x называется прообразом элемента 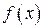 относительно отображения f. Множество X называется областью определения отображения f.
относительно отображения f. Множество X называется областью определения отображения f.
Определение 2.3. Пусть f – отображение множества X в множество Y , а множество A является подмножеством множества X. Множество 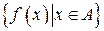 называется образом множества A при отображении f и обозначается
называется образом множества A при отображении f и обозначается 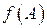 . В этом случае множество A называется прообразом множества
. В этом случае множество A называется прообразом множества 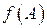 .
.
Пример. Пусть X – множество студентов потока, находящихся в аудитории на лекции, а Y – множество стульев, находящихся в этой аудитории. Рассмотрим отображение f, сопоставляющее каждому студенту стул, на котором он сидит (при условии, что все студенты на лекции сидят). Тогда стул, занимаемый студентом является образом данного студента при отображении f. Рассмотрим множество 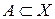 , A – множество студентов из одной определенной группы потока. Тогда
, A – множество студентов из одной определенной группы потока. Тогда 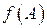 – множество стульев, занимаемых студентами из данной группы.
– множество стульев, занимаемых студентами из данной группы.
Определение 2.4. Отображение f множества X в множество Y называется функцией, если множество Y – числовое множество.
Определение 2.5. Отображение f множества X в множество Y называется сюръективным, или “отображением на”, если образом области определения X является все множество Y.
Отображение f множества X в множество Y называется инъективным, если для любых 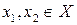 из условия
из условия 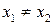 следует
следует 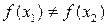 .
.
Отображение f множества X в множество Y называется биективным, если оно сюръективно и инъективно. Биективное отображение также называют взаимно однозначным соответствием.
Примеры. 1) В предыдущем примере отображение 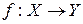 является инъективным, поскольку разным студентам соответствуют разные стулья. В случае, когда свободных стульев в аудитории нет, отображение также является сюръективным, а значит и биективным, то есть взаимно-однозначным соответствием между множеством студентов и множеством стульев. Если же в аудитории имеются незанятые стулья, то отображение сюръективным не является.
является инъективным, поскольку разным студентам соответствуют разные стулья. В случае, когда свободных стульев в аудитории нет, отображение также является сюръективным, а значит и биективным, то есть взаимно-однозначным соответствием между множеством студентов и множеством стульев. Если же в аудитории имеются незанятые стулья, то отображение сюръективным не является.
2) Пусть 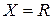 ,
, 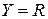 . Отображение
. Отображение 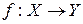 задается формулой:
задается формулой:
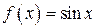 . Тогда отображение f является функцией. При этом оно не сюръективно (
. Тогда отображение f является функцией. При этом оно не сюръективно ( 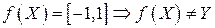 ). Оно также и не инъективно, так как разным значениям x могут соответствовать равные образы, например,
). Оно также и не инъективно, так как разным значениям x могут соответствовать равные образы, например, 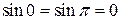 .
.
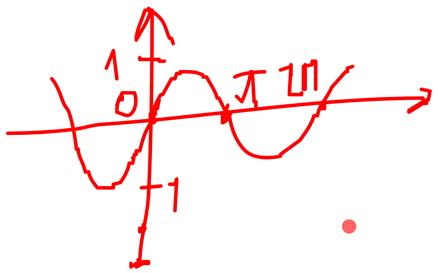
3) Пусть 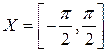 ,
, 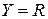 . Отображение
. Отображение 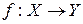 задается формулой:
задается формулой:
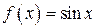 .Тогда данное отображение не сюръективно, но инъективно, поскольку на отрезке
.Тогда данное отображение не сюръективно, но инъективно, поскольку на отрезке 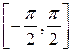 разным значениям x соответствуют разные образы
разным значениям x соответствуют разные образы 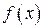 .
.
4) Пусть 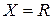 ,
, 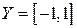 . Отображение
. Отображение 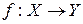 задается формулой:
задается формулой:
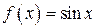 . В этом случае отображение f сюръективно, так как
. В этом случае отображение f сюръективно, так как 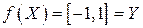 , но не инъективно.
, но не инъективно.
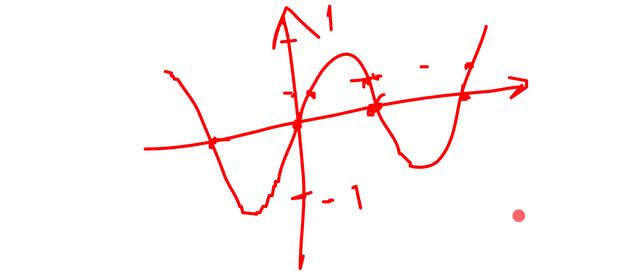
5) Пусть 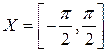 ,
, 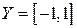 , Отображение
, Отображение 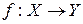 задается формулой:
задается формулой:
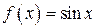 . В этом случае отображение f , очевидно, сюръективно и инъективно, следовательно, биективно.
. В этом случае отображение f , очевидно, сюръективно и инъективно, следовательно, биективно.
Сравнение множеств
Важной характеристикой множества является количество его элементов. Множество называется конечным, если оно состоит из конечного числа элементов, и бесконечным в противном случае. Любые два конечных множества можно сравнить по количеству их элементов, ответив на вопрос, в каком множестве элементов больше и на сколько. Для бесконечных множеств такое сравнение теряет смысл (в частности, невозможно определить на сколько отличаются количества элементов в множествах).
Определение 3.1. Говорят, что два множества имеют одинаковую мощность (равномощны), если между элементами этих множеств можно установить взаимно однозначное соответствие.
Иными словами, два множества равномощны, если каждому элементу одного из них можно поставить в соответствие ровно один элемент другого и наоборот.
Из определения следует, что конечные множества имеют одинаковую мощность в том и только том случае, когда они состоят из одинакового количества элементов.
Определение 3.2. Бесконечное множество называется счетным, если оно имеет одинаковую мощность с множеством натуральных чисел N.
Иначе говоря, множество счетно, если его элементы можно занумеровать с помощью натуральных чисел. Таким образом, чтобы установить счетность множества, нужно найти взаимно однозначное соответствие между элементами этого множества и множества N. Или, что то же самое, найти способ нумерации элементов данного множества натуральными числами.
Примеры. 1) Множество целых чисел Z счетно. Действительно, составим таблицу, в первой строке которой записаны целые числа, а во второй – их натуральные номера:
| Z | -1 | -2 | -3 | -4 | … | ||||
| N | … |
2) Пусть множества A и B счетны. Тогда их прямое произведение 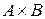 тоже счетно. Для доказательства этого составим бесконечную (вправо и вниз) таблицу, в которой каждой строке соответствует элемент множества A, а каждому столбцу – элемент множества B. В клетках таблицы поставим натуральные числа – номера элементов множества
тоже счетно. Для доказательства этого составим бесконечную (вправо и вниз) таблицу, в которой каждой строке соответствует элемент множества A, а каждому столбцу – элемент множества B. В клетках таблицы поставим натуральные числа – номера элементов множества 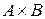 так, как показано стрелками. Очевидно, что таким образом каждому элементу
так, как показано стрелками. Очевидно, что таким образом каждому элементу 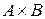 будет соответствовать свой определенный номер, причем разным элементам будут соответствовать разные номера. Это и доказывает счетность множества
будет соответствовать свой определенный номер, причем разным элементам будут соответствовать разные номера. Это и доказывает счетность множества 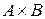 .
.
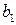
| 
| 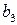
| 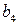
| … | |
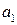
| 1 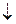
| 4 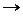
| 5 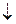
| 16 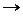
| |
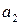
| 2 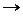
| 3 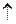
| 6 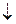
| 15 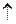
| |
| 9 
| 8 
| 7 
| 14 
| |
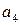
| 10 
| 11 
| 12 
| 13 
| |
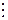
|
3) Множество рациональных чисел Q счетно. Для доказательства этого рассмотрим прямое произведение двух счетных множеств: 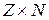 , оно, как было доказано в примере 2, счетно. Это значит, что каждой упорядоченной паре чисел
, оно, как было доказано в примере 2, счетно. Это значит, что каждой упорядоченной паре чисел 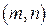 , где
, где 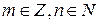 , можно присвоить натуральный номер. Тогда и каждой обыкновенной дроби
, можно присвоить натуральный номер. Тогда и каждой обыкновенной дроби 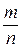 , можно присвоить натуральный номер, следовательно, множество обыкновенных дробей также счетно. Поскольку каждое рациональное число может быть представлено в виде различных обыкновенных дробей (например, рациональное число
, можно присвоить натуральный номер, следовательно, множество обыкновенных дробей также счетно. Поскольку каждое рациональное число может быть представлено в виде различных обыкновенных дробей (например, рациональное число 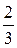 можно представить также в виде дробей
можно представить также в виде дробей 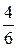 ,
, 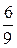 и т. д.), множество рациональных чисел Q можно отождествить с некоторым подмножеством множества обыкновенных дробей. А так как множество Q бесконечно, то оно, очевидно, счетно.
и т. д.), множество рациональных чисел Q можно отождествить с некоторым подмножеством множества обыкновенных дробей. А так как множество Q бесконечно, то оно, очевидно, счетно.
Рассмотрим теперь пример множества, которое не является счетным. Докажем, что интервал 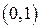 не является счетным.
не является счетным.
Предположим, что интервал 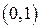 – счетное множество. Это значит, что все числа из
– счетное множество. Это значит, что все числа из 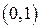 удалось каким-то образом занумеровать:
удалось каким-то образом занумеровать: 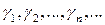 . Каждое такое число можно записать в виде бесконечной десятичной дроби:
. Каждое такое число можно записать в виде бесконечной десятичной дроби:
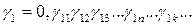 ,
,
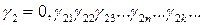 ,
,
…………………………….
…………………………….
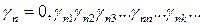 ,
,
где 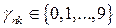 ,
, 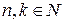 .
.
Напишем теперь десятичную дробь 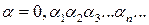 , цифры которой удовлетворяют условию:
, цифры которой удовлетворяют условию: 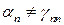 . Понятно, что тогда
. Понятно, что тогда 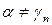 ни при каком
ни при каком 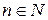 . Но с другой стороны
. Но с другой стороны 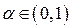 . Следовательно, нам не удалось занумеровать все числа из интервала
. Следовательно, нам не удалось занумеровать все числа из интервала 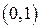 вопреки предположению.
вопреки предположению.
Этот пример показывает, что имеются множества, не являющиеся счетными.
Определение 3.3. Будем говорить, что множество действительных чисел, составляющих интервал 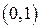 имеет мощность континуум, и все множества равномощные с интервалом
имеет мощность континуум, и все множества равномощные с интервалом 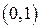 также имеют мощность континуум.
также имеют мощность континуум.
Примеры.
1) Очевидно, что любой интервал 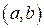 также имеет мощность континуум. Приведем пример взаимно однозначного соответствия интервалов
также имеет мощность континуум. Приведем пример взаимно однозначного соответствия интервалов 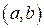 и
и 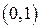 :
:
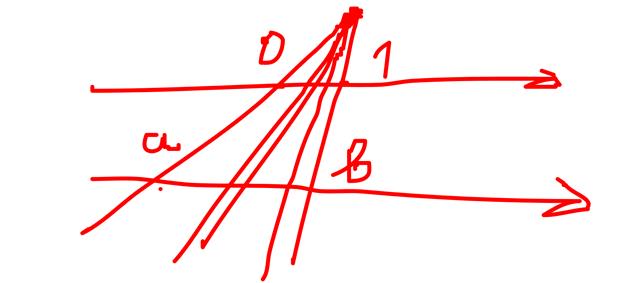
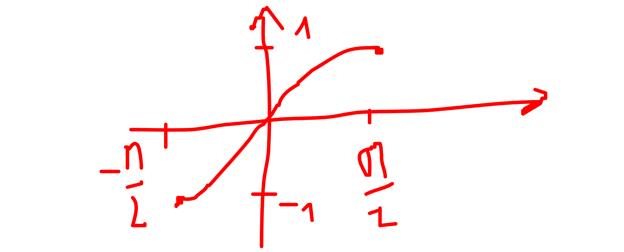
2) Множество всех действительных чисел R имеет мощность континуум. Действительно, взаимно однозначное соответствие между интервалом 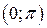 и множеством R можно установить, например, с помощью функции
и множеством R можно установить, например, с помощью функции 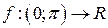 , которая каждому числу
, которая каждому числу 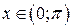 ставит в соответствие число y по формуле
ставит в соответствие число y по формуле 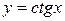 .
.
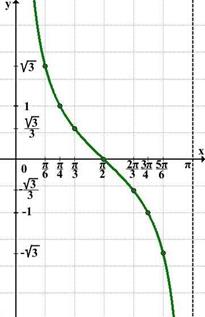
Из свойств этой функции следует, что она является взаимно однозначным соответствием, значит множества 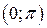 и R равномощны, а это и означает, что R имеет мощность континуум.
и R равномощны, а это и означает, что R имеет мощность континуум.
3. Полуинтервал 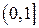 также имеет мощность континуум. Доказательство этого факта приведено в “Конспекте лекций по дискретной математике”.
также имеет мощность континуум. Доказательство этого факта приведено в “Конспекте лекций по дискретной математике”.
Можно доказать, что мощность континуум имеет и множество всех
точек плоскости, и множество точек пространства, и множество 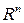 при всех
при всех 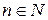 .
.
Дата добавления: 2021-02-19; просмотров: 728;











