Множества и операции над ними, их геометрическое истолкование

Понятие множества относится к числу первичных в математике: его нельзя определить через другие понятия. Для наших целей оказывается достаточным интуитивного представления о множестве, и поэтому можно ограничиться его описанием и примерами.

Множество состоит из элементов и полностью определяется ими. Принадлежность элемента a множеству A обозначают 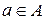; запись 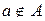означает, что a – не элемент A.

Множество можно задать либо непосредственным перечислением его элементов, либо указанием некоторого свойства, которым обладают элементы этого множества, и только они. В первом случае используют запись вида 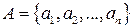( в фигурных скобках через запятую перечисляются элементы множества). Во втором случае записывают 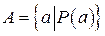, что означает, что множество A состоит из тех и только тех элементов, для которых выполняется свойство .

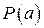Примеры 1.1

1) Запись вида 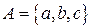означает, что множество A состоит из трех элементов a, b и c.

2) 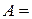{человек│человек является студентом СПбГЭУ}. Множество A – множество студентов СПбГЭУ.

Множество, не содержащее ни одного элемента, называется пустым и обозначается знаком .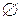

Два множества называются равными, если они состоят из одних и тех же элементов. Равенство множеств A и B обозначают: .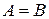

Множество A называется подмножеством множества B если каждый элемент множества A является элементом множества B. В этом случае также говорят, что имеет место включение множества A в множество B и обозначают 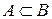(или ).

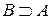При доказательстве включения одного множества в другое можно пользоваться формулой:

.

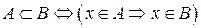Для любого множества A верно, что 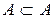и .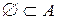

Очевидно, что 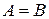тогда и только тогда, когда 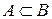и .

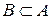При доказательстве равенства двух множеств можно пользоваться формулой:

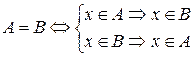
Операции над множествами

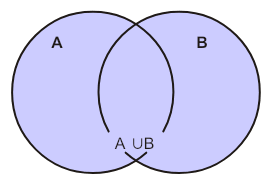
Объединением множеств A и B называется множество, обозначаемое 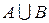, состоящее из элементов, каждый из которых принадлежит хотя бы одному из множеств A или B:

.

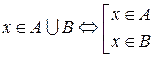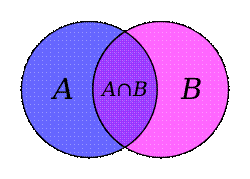
Пересечением множеств A и B называется множество, обозначаемое 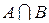, состоящее из элементов, каждый из которых принадлежит как множеству A, так и множеству B:

.

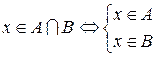Пример 1.2. Пусть 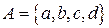и 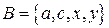. Тогда , .

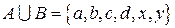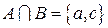Следующие свойства операций объединения и пересечения множеств следуют непосредственно из определений:

1) Коммутативность объединения и пересечения множеств

(переместительный закон):

; .

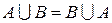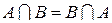2) Ассоциативность объединения и пересечения множеств

(сочетательный закон):

; .

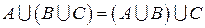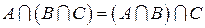3) ; .

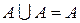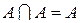4) ; .

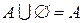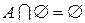Следующие два свойства называются дистрибутивностью объединения и пересечения множеств (распределительным законом):

5) .

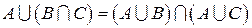6) .

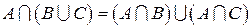Замечание. Для обозначения объединения множеств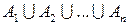

используют обозначение . Аналогичное обозначение используют для пересечения множеств: .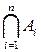

Разностью множеств A и B (или дополнением множества B в

множестве A) называется множество, обозначаемое A\B, состоящее из элементов множества A, не входящих в множество B:

A\B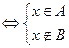

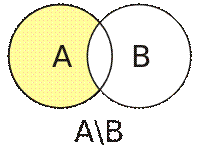
Пример1.3. Пусть 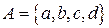и 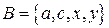. Тогда A\B 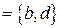, B\A .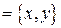

Операции с множествами – объединение, пересечение и разность (дополнение) – связаны между собой так называемыми соотношениями двойственности: дополнение к объединению множеств равно пересечению их дополнений, а дополнение к пересечению – объединению дополнений. Действительно, пусть A, B и C – три множества. Докажем, что:

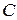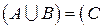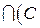\ \A) \B).

Пусть 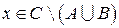. Это означает, что

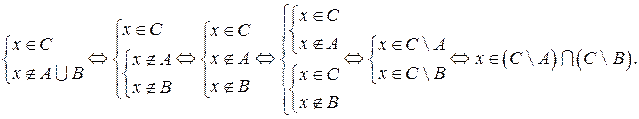Второе соотношение двойственности: 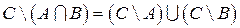доказывается аналогично.

Будем считать, что все множества в рассматриваемой задаче содержатся в одном и том же множестве U (универсальном множестве). Тогда дополнение множества A в множестве U будем обозначать .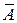

В этих обозначениях соотношения двойственности принимают вид:

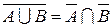и ,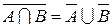

и известны как формулы де Моргана.

Прямым (декартовым) произведением двух множеств A и B называется множество, обозначаемое 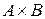, элементами которого являются упорядоченные пары 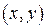, где :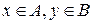

.

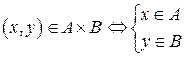Пример 1.4. 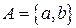, 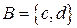. Тогда 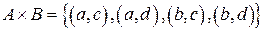и .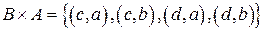

Пример 1.5. 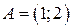, 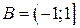. На рисунке изображены множества 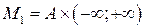, 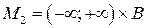. Двойной штриховкой обозначено множество .

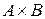Числовые множества

Перечислим общепринятые обозначения числовых множеств.

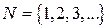– множество натуральных чисел.

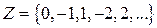– множество целых чисел.

Q – множество рациональных чисел. Рациональным числом называется число, которое может быть представлено в виде отношения 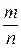, где , .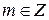

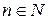R – множество действительных чисел.