Модели экономического роста

Существует множество моделей экономического роста. Рассмотрим только основные.

В своей модели американский экономист и социолог У. Ростоу выделил пять стадий роста:

1. Стадия классового (традиционного) общества характеризуется статическим равновесием, доньютоновской наукой и техникой, аграрным хозяйством, ограниченными возможностями развития производительных сил, падением доходов из-за низких темпов экономического роста, с одной стороны, и большой рождаемостью – с другой, последующей стабилизацией численности населения и доходов в соответствии с законом народонаселения Р. Мальтуса. На этой стадии практически нет условий для сколько-нибудь расширенного воспроизводства национального продукта.

2. Переходное общество. Эта стадия в развитии общества характеризуется подготовкой условий для последующего его сдвига с состояния статического равновесия. Такой сдвиг становится возможным благодаря тому, что годовая норма накопления в национальном доходе поднимается до 5%. Примером такого общества может быть Европа конца XVII в.

3. Стадия «разбега» и перехода к индустриальному развитию. На этой стадии доля инвестиций повышается до 10% годового национального дохода. Помимо роста третья стадия имеет еще два отличительных свойства. Должна существовать, по крайней мере, одна значительная отрасль промышленности с высокими темпами роста, а также политическая или общественная структура, поддерживающая расширение этой отрасли. У. Ростоу определил стадию «разбега» как промышленную революцию. Она охватывает сравнительно небольшой промежуток времени: 20-30 лет.

4. «Путь к зрелости». Аналогом этой стадии является индустриальное общество, развитие которого характеризуется увеличением нормы накопления до 20% национального дохода. Обычно эта стадия продолжается 60 лет. У. Ростоу считал началом этого периода для: Великобритании – 1850 г., Швеции – 1930 г., США – 1900 г., Японии – 1940 г., Германии – 1910г., России – 1950 г., Франции – 1910г., Канады – 1950 г.

В этот период развивается процесс урбанизации, повышается доля квалифицированного труда, руководство промышленностью сосредотачивается в руках квалифицированных управляющих – менеджеров.

5. Стадия массового потребления. Ее характеризует такое состояние в экономике, когда производственный потенциал нации начинает работать преимущественно на потребителя, а ведущим сектором экономики выступают отрасли, производящие предметы длительного пользования. Это самая продолжительная стадия. У. Ростоу считал, что США потребовалось около 100 лет для перехода от зрелости к стадии массового потребления.

В своей более поздней работе «Политика и стадии роста» У. Ростоу выступил с концепцией шестой стадии роста – «поиска качества жизни», в которой ведущим сектором экономики становится сфера услуг, а на первый план общественного прогресса выдвигается духовное развитие человека.

Неокейнсианские модели экономического роста

1. Основываются на главном постулате Дж. Кейнса – совокупном спросе. При построении моделей их авторы исходили из того, что решающим условием сбалансированного роста экономики является увеличение совокупного спроса.

2. Основным фактором экономического роста считаются капиталовложения (инвестиции), которые посредством мультипликатора расширяют прибыль или сами вызваны ростом прибыли (под воздействием акселератора). Все остальные производственные факторы (увеличение занятости, степень использования оборудования, улучшение организации производства) в расчет не берутся и исключаются из модели.

Модель экономического роста Е. Домара

Е. Домар уточнил и дополнил теорию Дж. Кейнса тем, что у него инвестиции являются фактором не только образования доходов, но и создания мощностей, и, следовательно, развития производства, и предложения товаров.

Таким образом, Е. Домар обратил внимание на двойственность инвестиционного процесса и считал, что в этом заключается смысл модели уравновешенного (сбалансированного) роста национального дохода. Далее Е. Домар поставил вопрос: если инвестиции увеличивают производственные мощности, а также создают дополнительные доходы, то как должны расти инвестиции, чтобы темп прироста дохода равнялся темпу прироста производственных мощностей?

Чтобы ответить на этот вопрос. Е. Домар составил систему трех уравнений:

1. Уравнение предложения показывает, какой прирост производственных мощностей (производства) создают инвестиции. Прирост производства ∆Q, получаемый за счет созданных производственных мощностей, можно определить путем умножения общих капиталовложений I на их среднюю производительность 𝛽.

Символ 𝛽, характеризующий влияние инвестиций на развитие производства, получил название капиталоотдачи (увеличение занятости рабочей силы, научно-технический прогресс, совершенствование организации производства и т. д.). Следовательно,

𝜷=∆𝑸/𝑰 (15.2)

2. Уравнение спроса показывает, на какую величину должен возрасти спрос, чтобы занять дополнительные мощности. Согласно теории мультипликатора, при любой предельной склонности к сбережению а прирост национального дохода ∆Y является результатом мультипликационного воздействия дополнительных инвестиций∆𝐼

∆Y=∆𝑰*𝟏/m, (15.3)

где 1/m − мультипликатор.

Если сравнить уравнение предложения и уравнение спроса, то нетрудно заметить, что в уравнении предложения ∆𝑸=𝜷𝑰 выступают общие инвестиции, в то время как в уравнении спроса – только прирост инвестиций по сравнению с предыдущим периодом. Это oбъясняется тем, что прирост производства ∆𝑸 обеспечивается производительностью всего капитала, тогда как прирост дохода ∆Y — лишь мультипликационным воздействием дополнительных капиталовложений.

3. Уравнение равенства темпов прироста дохода и производственных мощностей достигается, когда

∆𝑰*𝟏/m= 𝜷𝑰 (15.4)

Решением этого уравнения устанавливается, что

∆𝑰/𝑰=m𝜷 (15.5)

В левой части уравнения стоит годовой темп роста инвестиций, которые для поддержания полной занятости с помощью увеличения производственных мощностей должны расти с годовым темпом Доход должен расти с тем же темпом. Из полученной формулы следует, что сбалансированный темп роста инвестиций является произведением склонности к сбережениям и степени производительности инвестиций.

Таким образом, модель Домара позволяет определить тот темп, с которым должны постоянно расти инвестиции. Этот темп находится в прямой зависимости от доли сбережений в национальном доходе (предельной склонности к сбережениям) и средней эффективности инвестиций.

Отсюда следовал важный вывод для экономической политики: только постоянно растущая аккумуляция капитала (рост инвестиций) обеспечивает в масштабе общества динамичное равновесие между совокупным спросом и совокупным предложением. Для поддержания сбалансированного роста инвестиций государство может воздействовать на долю сбережений (накопления) в национальном доходе или на темпы технического прогресса (производительность капитала).

Модель Экономического роста Р. Харрода

Целью модели Р. Харрода является исследование траектории роста экономики. Поэтому ее основу составляет теория акселератора, позволившая определить отношение прироста инвестиций к вызвавшему его приросту дохода.

Если Домар оперировал только так называемыми автономными (независимыми от дохода) инвестициями, связанными с соответствующей государственной политикой, то как Р. Харрод – производными (индуцированными) инвестициями, вызванными ростом национального дохода. Вспомним принцип акселератора.

Принцип акселератора показывает, что возросшие доход и спрос, в свою очередь, ускоряют инвестиционный процесс, Это означает, что новые капиталовложения – функция прироста дохода, умноженного на коэффициент акселерации 𝛿

∆𝑰=∆𝒀𝜹 (15.6)

Коэффициент акселерации – техническая величина, зависящая от типа технического прогресса, обладает следующими свойствами:

• при капиталоемком техническом прогрессе, требующем больших объемов капитала, значение 𝛿 растет;

• при техническом прогрессе, экономящем капитал (капиталосберегающий тип), значение 𝛿 становится меньше.

При создании модели экономического роста Р. Харрод ввел в анализ три уравнения:

1. Уравнение фактического темпа роста – исходное уравнение модели Р. Харрода. Оно показывает, какой должна быть доля сбережений в национальном доходе, чтобы обеспечить накопление части прироста продукции, идущей на производственные цели:

Gc=s, (15.7)

где G – фактический прирост (growth – рост) общего выпуска за какой-либо период, например за год:

G=∆𝒀/𝒀, то есть фактический темп роста – это отношение приращения дохода к величине дохода базового периода;

C – капитальный коэффициент (capital – капитал), или коэффициент капиталоемкости производства, показывающий "инвестиционную цену" одной единицы прироста дохода или продукции и являющийся величиной, обратной производительности капитала. c=𝐼/∆𝑌 при этом 𝛽=1/с;

S – доля сбережений в национальном доходе, или склонность к сбережению ( s=𝑆/𝑌).

Если в уравнение (15.7) подставить значение его элементов, то получим известное равенство Дж. Кейнса – инвестиции равны сбережениям.

2. Уравнение гарантированного темпа роста выражает равновесие непрерывного поступательного движения, то есть прогнозируемую линию развития, на которую настраиваются предприниматели и которой они в целом удовлетворены :

Gwcr=s (15.8)

Р. Харрод считал, что гарантированный (warranted) темп роста Gw является линией динамического равновесия.

сr – требуемый коэффициент капиталоемкости также является категорией динамического равновесия: он выражает потребность в новом капитале, деленную на прирост выпуска продукции, для обеспечения которого требуется этот новый капитал.

Следовательно, в уравнении гарантированного темпа роста приравниваются инвестиции ex-ante и сбережения ex-post.

Поскольку доля сбережений в национальном доходе s – величина постоянная (из-за постоянства мотивов, побуждающих людей совершать сбережения), как и требуемый коэффициент капиталоемкости сr, то отсюда Р. Харродом делался вывод о постоянном уровне гарантированного темпа роста Gw .

Если бы фактический темп роста совпадал с прогнозируемым, гарантированным темпом , то экономика имела бы устойчивое непрерывное развитие. Однако, такой устойчивости нет ни в статическом (краткосрочном), ни в динамическом (долгосрочном) плане.

Сравнивая оба уравнения Харрод отмечает, что на практике фактический темп роста всегда выше или ниже гарантированного. Если фактический темп превысит гарантированный, то s из-за относительного постоянства не сможет немедленно увеличиться в той же степени, а это значит, что фактический коэффициент капиталоемкости с обязательно понизится и станет меньше требуемого (прогнозного) коэффициента капиталоемкости, на который ориентировались предприниматели.

Иными словами, если G>Gw и s=const, то с<cr. Отсюда Р. Харрод делает вывод, что производители, оценивая фактическую капиталоемкость как чрезмерно низкую, постараются увеличить товарно-материальные запасы, закупить новое оборудование, что повлечет за собой еще большее превышение фактического темпа роста над гарантированным (равновесным).

Если же G<Gw , то c>cr на основании чего производители сделают вывод о том, что имеющиеся у них запасы сырья, материалов и оборудования чрезмерны, сократят закупки, чем еще больше снизят фактический темп роста по сравнению с гарантированным.

Таким образом, мы видим, что вместо приспособления фактического темпа развития производства к равновесному на практике имеет место обратная тенденция – к все большему удалению производства от линии динамического равновесия либо в сторону повышения, либо в сторону понижения.

Это дало основание Р. Харроду сделать вывод о том, что рыночная экономика «балансирует на острие ножа», что ей внутренне присуща динамическая нестабильность, что внутри ее «работают центробежные силы, заставляя систему все дальше и упорнее отклоняться от требуемой линии развития». Данный вывод впоследствии получил в экономической литературе наименование «парадокс Харрода».

Он, как видим, объясняет кратковременные циклические колебания экономической конъюнктуры. Для интерпретации более длительных колебаний экономической динамики Р. Харрод вводит третье уравнение – уравнение естественного темпа роста.

3. Уравнение естественного темпа роста в модели Р. Харрода имеет следующий вид:

Gncr= или ≠𝒔, (15.9)

где Gn – (natural – естественный) максимально возможный темп движения экономики при полном использовании ресурсов.

Для поддержания такого темпа роста в экономике может не хватить сбережений, поэтому в уравнении естественного темпа роста предусматривается отсутствие обязательного равенства между левой и правой частями (заметим, что гарантированный темп роста Gw допускал наличие и вынужденной безработицы).

Выведенные уравнения позволили Р. Харроду рассмотреть соотношение между тремя величинами: естественным Gn, гарантированным Gw и фактическим G темпами роста.

1. Если Gw > Gn. В этом случае, так как естественный темп роста максимально возможен при данных ресурсах, фактический будет ниже естественного, а значит, окажется обязательно ниже и гарантированного. Тогда прогнозный коэффициент капиталоемкости будет ниже фактического (сr<с), что приведет, как было показано выше, к длительной депрессии. На более понятном языке это означает, что чрезмерное перенапряжение сил ("перегрев экономики") порождает длительную фазу спада.

2. Если Gw < Gn, то возможны два сценария развития экономики. Первый (Gw > G), рассмотренный выше, ведет к продолжительной депрессии, второй (поскольку из Gw <G следует, что сr > с) может характеризоваться периодом длительного бума.

Следовательно, отношение между естественным и гарантированным темпами роста имеет решающее значение для определения того, будет ли на протяжении ряда лет преобладать оживление или депрессия.

Таким образом, Харрод обращает внимание на две проблемы в экономической динамике:

1) расхождение между Gw и Gn

2) удаление G от Gw ,

- первая проблема есть проблема хронического избытка рабочей силы,

- вторая – это проблема хронического ее недостатка.

Затем Харрод ставит следующий вопрос: существуют ли в рыночной экономике силы, которые бы автоматически уравнивали гарантированный Gw и естественный Gn темпы роста? Отвечая на него, Р. Харрод указывал, что главным параметром экономического роста, зависящим от воли людей, являются сбережения, и поэтому исследование этого вопроса сводится к исследованию динамики сбережений. При этом он, однако, задавался вопросом: существуют ли в рыночной экономике инструменты, автоматически стимулирующие такой размер сбережений, который соответствовал бы требованиям сбалансированного роста? Р. Харрод отвечал на него отрицательно и вслед за Дж. Кейнсом обосновывал необходимость государственного вмешательства в экономику.

Программа государственного вмешательства в экономику у Р. Харрода включала две группы мероприятий:

а) против «бегства фактического темпа роста от гарантированного» предлагалась антициклическая политика краткосрочного плана (общественные работы, процентная ставка, создание "буферных запасов" из непортящихся материалов, сырья, продовольствия); государственные органы должны поддерживать цены на такие товары на относительно стабильном уровне путем массовой их закупки во время спада и распродажи – во времена бума;

б) против хронической безработицы и длительной депрессии предлагалось использовать политику снижения нормы процента – вплоть до нулевой отметки. Это приведет к расширению инвестиционного спроса на сбережения (на величину d), а значит, к некоторому сокращению доли сбережений в национальном доходе.

Цель политики государственного вмешательства, по словам Р. Харрода, должна состоять в достижении такого прогрессирующего понижения процентной ставки, при котором: Gwcr = s-d =Gncr.

Данное выражение Р. Харрод определил как формулу устойчивого роста при полной занятости. Она показывает, что устойчивое динамическое развитие экономической системы (стабильный характер фактического темпа роста) достигается при равенстве гарантированного и естественного темпов роста в условиях полной занятости ресурсов.

Модель Р. Солоу

Модель построена на неоклассической предпосылке господства совершенной конкуренции на рынках факторов производства, обеспечивающей полную занятость ресурсов. Выпуск продукции – функция не только капитала, но и труда, которые являются хорошими субститутами, и сумма коэффициентов эластичности выпуска по этим факторам равна единице.

Сначала модель описывает равновесие экономической системы при нейтральности технического прогресса и постоянной отдаче от масштаба, в дальнейшем в нее вводятся технологические сдвиги посредством изменения нормы накопления и убывающей отдачи от масштаба.

Р. Солоу исходит из того, что необходимым условием равновесия экономической системы является равенство совокупного спроса и совокупного предложения. При этом совокупное предложение в его модели определяется на основе производственной функции Кобба–Дугласа, выражающей отношение функциональной зависимости между объемом производства, с одной стороны, и используемыми факторами и их взаимной комбинацией – с другой. Производственная функция Кобба–Дугласа обладает тем свойством, что доли каждого фактора в стоимости продукта постоянны, хотя в абсолютном выражении затраты труда и капитала могут изменяться

Y=AK𝛼L𝛽, (15.10)

где 𝛼+𝛽=1

В развернутом виде данная функция У Солоу принимает вид:

Y=(∆𝒀⁄∆𝑳)L+(∆𝒀⁄∆𝑲)K, (15.11)

где ∆𝒀⁄∆𝑳 – предельный продукт труда MPL;

∆𝒀⁄∆𝑲– предельный продукт капитала МРК.

Это означает, что общий продукт (выпуск) равняется сумме произведений затраченного количества труда L и капитала К на их предельные продукты, т. е. на приросты продуктов ∆𝒀 от увеличения затрат труда ∆𝑳 и затрат капитала ∆𝑲. Для упрощения функции обозначим:

y=𝒀⁄𝑳, ….(15.12)

k=𝑲⁄𝑳, (15.13)

где у – выпуск продукции в расчете на одного работника, или производительность /труда;

к – капиталовооруженность (фондовооруженность) труда.

Тогда производственную функцию можно записать:

y=f(k) (15.14)

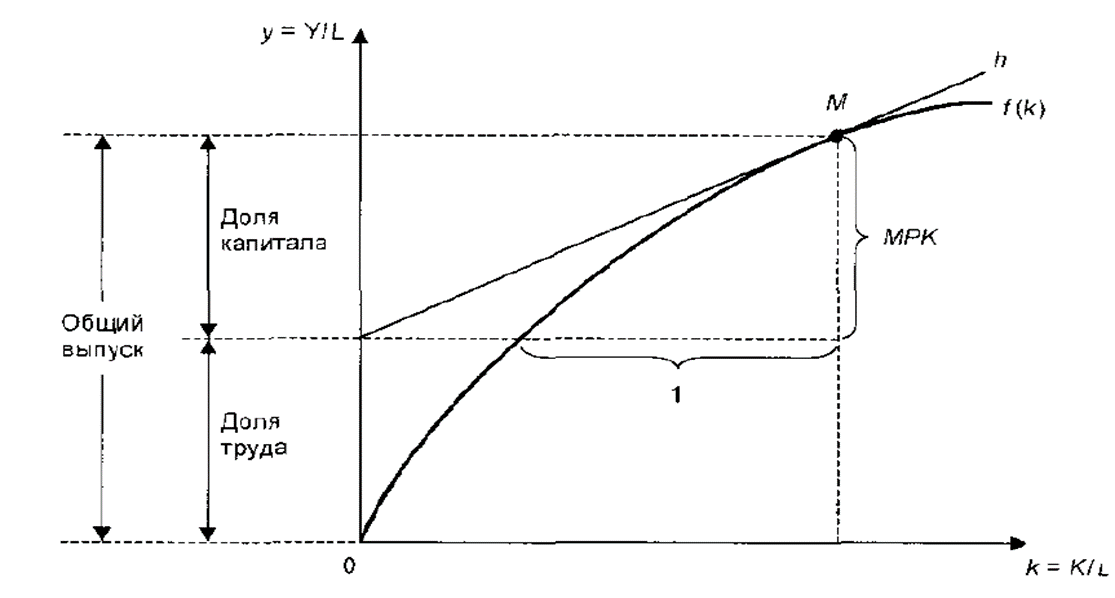
Рисунок 15.2. – Функциональная зависимость выпуска от доли труда и капитала

График показывает, что капиталовооруженность k определяет размер выпуска продукции в расчете на одного работника: Тангенс угла наклона касательной h равен предельной производительности капитала: если к увеличивается на одну единицу, то у возрастает на МРК единиц. При этом мы видим, что по мере роста капиталовооруженности труда его производительность увеличивается, но с убывающей скоростью, поскольку предельная производительность капитала снижается

Совокупный спрос в модели Р. Солоу определяется инвестиционным и потребительским спросом (государственные закупки для простоты не учитываются). Уравнение выпуска в расчете на одного работника примет вид:

y=c+i, (15.15)

где c и i – потребление и инвестиции в расчете на одного занятого.

Поскольку доход используется на потребление и сбережения в соответствии со сложившейся склонностью к сбережению, то функцию потребления можно представить как

c=(1-s)y , (15.16)

где s – норма сбережения (накопления).

Тогда y=c+i= (1-s)y+i

i=sy

Иначе говоря, в условиях равновесия инвестиции равны cбережениям и пропорциональны доходу.

В результате условие равенства спроса и предложения может быть представлено как:

f(k)=c+i или f(k)=𝒊⁄𝒔.

Производственная функция определяет предложение на рынке товаров, а накопление капитала – спрос на произведенную продукцию.

Теперь посмотрим, как накопление капитала обеспечивает экономический рост. Объем капитала меняется под воздействием инвестиций и выбытия: инвестиции увеличивают запас капитала, выбытие – уменьшает.

Инвестиции в расчете на одного работника являются частью дохода, приходящегося на одного работника, так что, заменив у выражением производственной функции, получим уравнение инвестиций как функцию от капиталовооруженности:

i=sf(k), (15.17)

Из уравнения следует, что чем выше уровень капиталовооруженности, тем выше уровень производства и больше инвестиции. Это свидетельствует о наличии связи между существующими запасами капитала к и накоплением нового капитала i что иллюстрирует следующий рисунок.

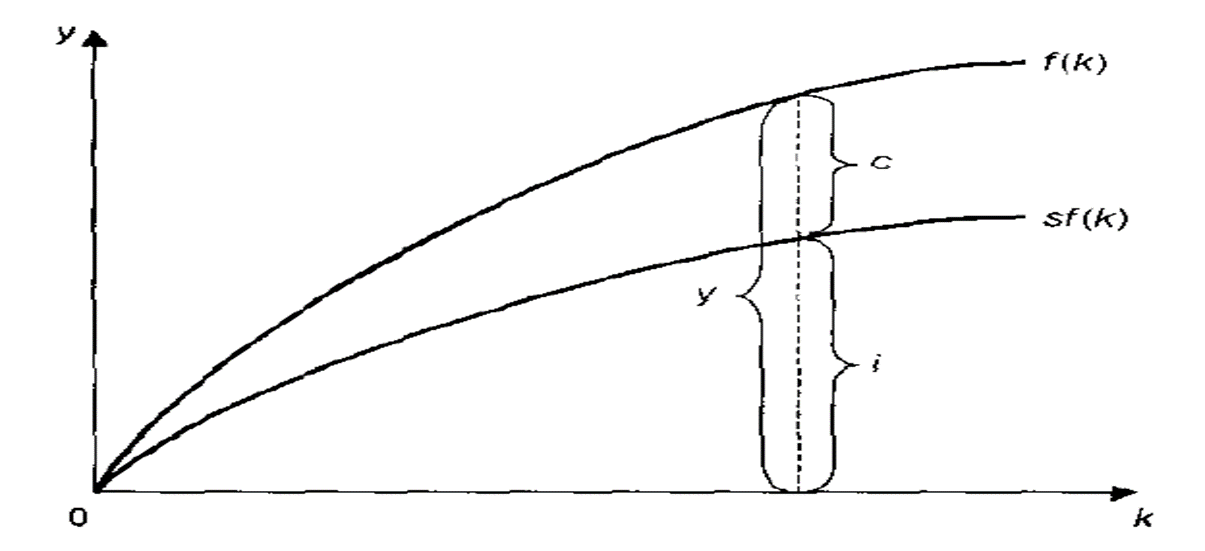
Рисунок 15..3 – Функциональная зависимость выпуска от капиталовооруженности

Норма сбережений s определяет деление произведенного продукта на потребление с и инвестиции i.

Для любого уровня капиталовооруженности к объем производства составляет f(k) инвестиции – sf(k) , а потребление соответственно f(k) – sf(k)

Для определения объема амортизации капитала допустим, что ежегодно выбывает определенная его доля d, называемая нормой амортизации. Например, если капитал эксплуатируется 10 лет, то норма выбытия равна 10% в год (d = 0,1). Таким образом, количество капитала, которое выбывает каждый год, составляет dk. Ежегодно выбываемая часть капитала пропорциональна запасам капитала.

Таким образом, влияние инвестиций и выбытия на запасы капитала можно выразить следующей формулой:

∆𝒌=𝒊−𝒅𝒌,……(15.18).

где ∆𝒌 – изменение запасов капитала, приходящееся на одного работника.

Используя равенство инвестиций и сбережений, получим:

∆𝒌= sf(k)- 𝒅𝒌

Оно показывает, что запас капитала к будет увеличиваться (∆𝒌>0) до уровня, пока инвестиции не уравняются с объемом выбытия sf(k) = 𝒅𝒌.

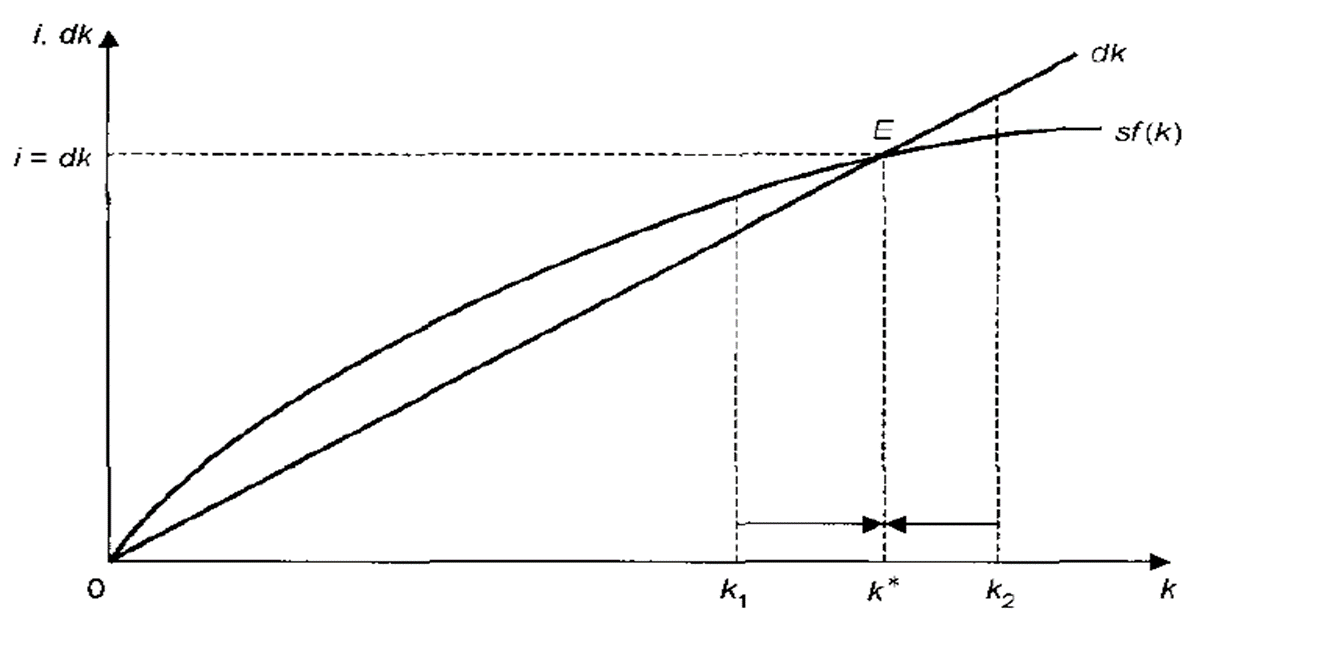
Рисунок 15.4. – Долгосрочное равновесие экономики при определенном равновесный уровне капиталовооруженности труда

Это состояние изображает точка Е, которой соответствует устойчивый (равновесный) уровень капиталовооруженности труда k*При достижении k* экономика находится в состоянии долгосрочного равновесия. Независимо от первоначального объема капитала, с которого экономика начинает развиваться, она затем достигает устойчивого состояния. Если запасы капитала ниже устойчивого уровня инвестици превышают выбытие (k1), капиталовооруженность увеличивается и будет расти, пока не приблизится к уровню k*. Если запасы капитала соответствуют точке k2 то инвестиции меньше, чем износ, а значит, запасы капитала будут сокращаться, приближаясь к уровню k*.

На равновесный уровень капиталовооруженности оказывает влияние норма накопления (сбережения). Ее рост с сдвигает кривую инвестиций с и экономика переходит в новое равновесное состояние с большей капиталовооруженностью и более высокой про изводительностью труда.

Таким образом, модель Солоу показывает, что норма сбережения (накопления) – ключевой фактор, определяющий уровень устойчивой капиталовооруженности. Более высокая норма сбережения обеспечивает больший запас капитала и более высокий уровень производства.

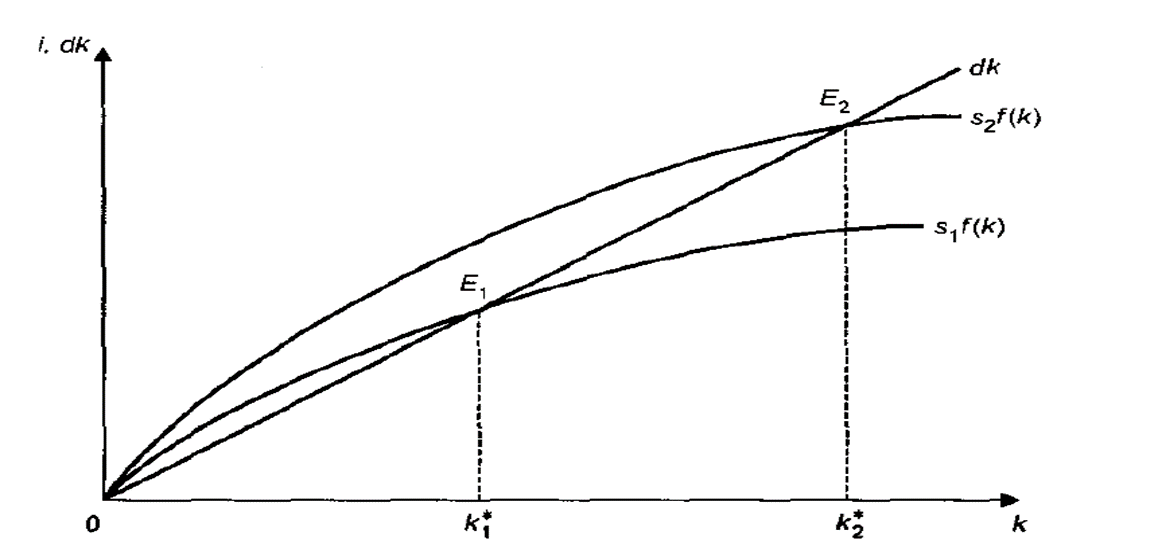
Рисунок 15.5. – Динамика долгосрочного равновесия экономики при росте капиталовооруженности труда

Процесс накопления как результат повышения нормы сбережения не объясняет механизма экономического роста, а лишь показывает переход от одного равновесного состояния к другому. Поэтому дальнейшее развитие модели Солоу предполагает изменение численности населения (занятых работников) и ускорения технического прогресса. Сначала введем фактор роста населения.

Равновесный уровень капиталовооруженности при росте населения. Предположим, население растет с постоянным темпом n. Очевидно, что увеличение численности работников при прочих равных условиях приведет к сокращению капиталовооруженности труда. В результате, уравнение, показывающее изменение запаса капитала на одного работника, будет выглядеть следующим образом:

∆𝒌= sf(k)- 𝒅𝒌-nk = i-𝒅𝒌-nk = i- (d+n)k………………(15.19)

Поскольку капиталовооруженность труда снижается (так как запас капитала распределяется между возросшим числом занятых), то для поддержания его на прежнем уровне необходим такой объем инвестиций, который не только покрывал бы выбытие капитала, но и обеспечивал бы капиталом новых работников в том же объеме, что и старых.

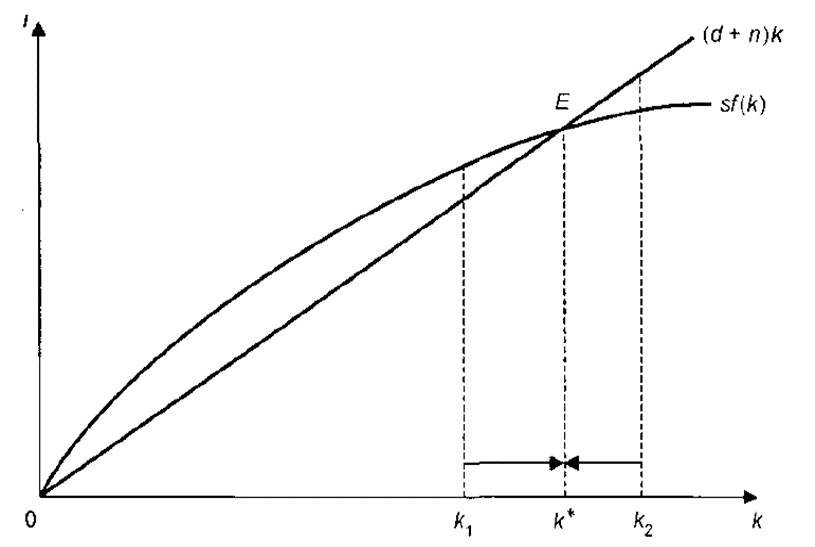
Рисунок 15.6. – Равновесие экономики при росте трудовых ресурсов

Математически это требование, характеризующее устойчивое равновесие в экономике при неизменной капиталовооруженности к*, примет вид:

∆𝒌= sf(k)- (d+n)k =0 → sf(k)= (d+n)k ……(15.20)

Составляющая (d+n)k в уравнении характеризует критическую величину инвестиций – такой их объем, который необходим для поддержания капитала, приходящегося на одного работника, на постоянном (неизменном) уровне.

Чтобы изобразить графически модель Р. Солоу с учетом роста населения, обозначим устойчивый уровень капиталовооруженности труда k*. Экономика будет находиться в равновесном состоянии, если капитал на одного работника k=const. Если k1<k*, то фактические инвестиции больше их критической величины и k1растет.

Если k2>k*, то инвестиции меньше их критического уровня и k2 падает.

Модель показывает, что. для того чтобы экономика находилась в устойчивом состоянии, инвестиции sf(k) должны компенсировать последствия выбытия капитала и роста населения (d+n)k, что имеет место в точке Е.

В этом случае капиталовооруженность и производительность труда у остаются неизменными. Но постоянство капиталовооруженности при росте населения означает, что капитал должен возрастать с тем же темпом, что и население, то есть ∆𝒀/𝒀=∆𝑲/𝑲=∆𝑳/𝑳=𝒏.

Отсюда следует вывод: рост населения – одна из причин непрерывного экономического роста в условиях устойчивого состояния экономики.

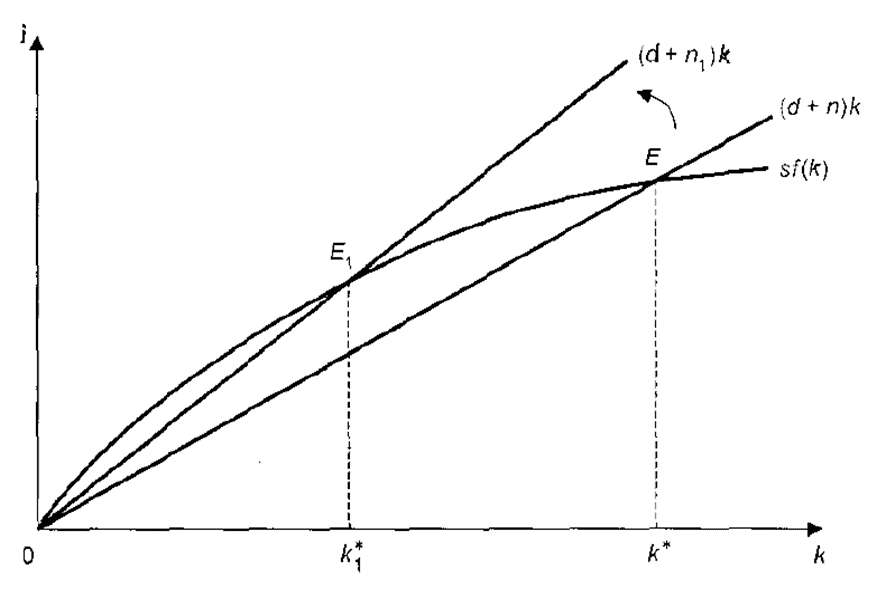
Рисунок 15.7. – Динамика долгосрочного равновесия экономики при росте трудовых ресурсов

Если рост населения не сопровождается увеличением инвестиций, то это ведет к уменьшению запаса капитала на одного работника.

Рост населения с n до n1, сдвигает линию (d + n)k вверх, в положение (d + n1)k что сокращает капиталовооруженность с k* до k1*.

Таким образом, модель Р. Солоу объясняет, что страны с более высокими темпами роста населения имеют меньшую капиталовооруженность, а значит – более низкие доходы.

Третьим источником экономического роста после инвестиций и увеличения численности занятых является технический прогресс. В неоклассической теории под техническим (технологическим) прогрессом понимается не машинизация производства (замена живого труда машинами), а качественные изменения в производстве (повышение образовательного уровня работников, улучшение организации, рост масштабов производства и т. п.).

Включение в модель технического прогресса изменит исходную производственную функцию, и она примет вид:

Y=f(K,L𝛆),………(15.21)

где ε – эффективность труда одного работника (зависит от здоровья, образования и квалификации рабочей силы);

Lε – численность эффективных единиц рабочей силы.

Технический прогресс вызывает прирост эффективности с постоянным темпом g. Поэтому если g = 2%, то отдача от каждой единицы труда увеличится на 2% в год, а это равносильно тому, что объем производства возрастет так, как если бы рабочая сила за год выросла на 2%. Такая форма технического прогресса называется трудосберегающей, a g – темпом трудосберегающего технического прогресса.

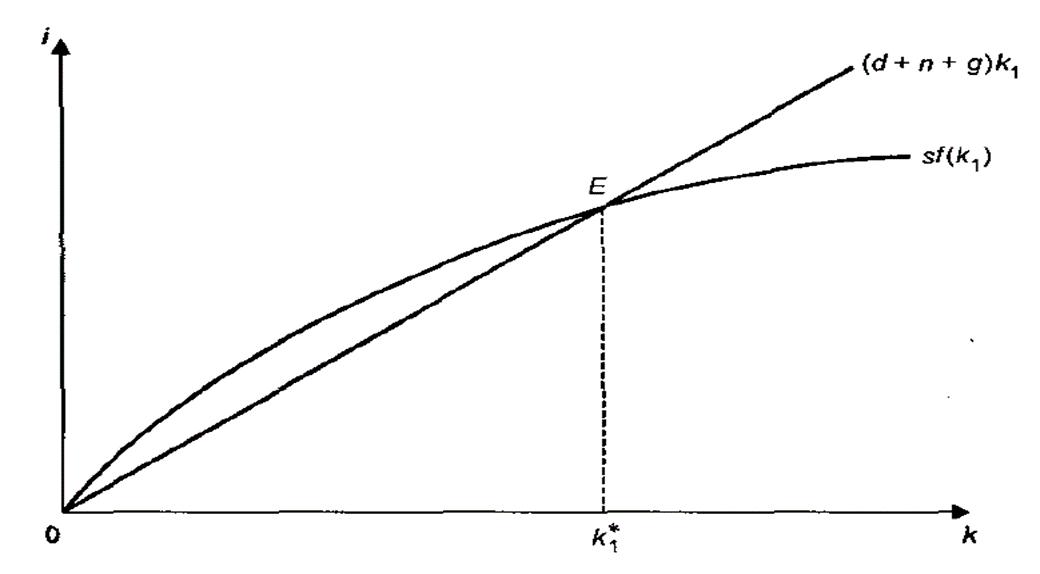
Рисунок 15.8. – Экономический рост экономики при росте технологии

Если численность занятых L растет с темпом n, а эффективность s растет с темпом g, то Lε будет увеличиваться с темпом n+ g. Капитал на единицу труда с постоянной (начальной) эффективностью составит k1= 𝐾/("L" ε), а объем производства на единицу труда с постоянной эффективностью y1= 𝑌/("L" ε).

Состояние устойчивого равновесия в этом случае будет достигаться при условии:

sf(k1)= (d+n+g)k1………(15.22)

Равенство показывает, что существует лишь один уровень капиталовооруженности, при котором капитал и выпуск, приходящиеся на единицу труда с неизменной эффективностью, постоянны. Это устойчивое состояние представляет собой долгосрочное равновесие экономики.

В устойчивом состоянии при наличии технического прогресса общий объем капитала К и выпуск Y будут расти с темпом n +g. В расчете на одного работника капиталовооруженность K/L и выпуск Y/L будут расти с темпом g. Это говорит о том, что технический прогресс в модели Солоу – единственное условие непрерывного роста уровня жизни.

Таким образом, модель Р. Солоу позволяет раскрыть взаимосвязь трех источников экономического роста – инвестиций, численности рабочей силы и технического прогресса. Воздействие государства на экономический рост возможно через его влияние на норму сбережения (накопления) и на скорость технического прогресса.

Равновесный экономический рост совместим с различными нормами сбережения, поэтому оптимальной будет считаться норма, обеспечивающая экономический рост с максимальным уровнем потребления. Такая норма соответствует "золотому правилу". Устойчивый уровень капиталовооруженности, соответствующий этой норме накопления, обозначим к**, а потребления – с**.

Произведенная продукция расходуется на потребление и инвестиции: y = c + i,откуда следует:c=y-i.

Подставляя значение данных параметров, которые они имели в устойчивом состоянии, получаем: с*=f(k*)-dk*,

где с* – потребление в состоянии устойчивого роста.

Устойчивый уровень капиталовооруженности, при котором максимизируется объем потребления, соответствует “золотому правилу". Капиталовооруженность по «золотому правилу» обозначена к**, а потребление по "золотому правилу" – с**.

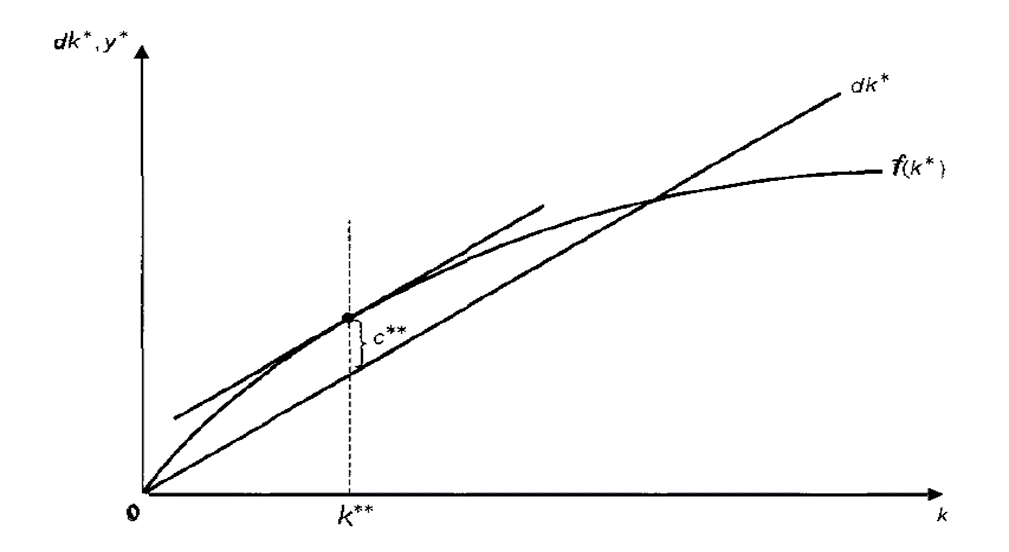
Рисунок 15.9. – Производственная функция, обеспечивающая максимально возможное потребление при данном уровне технологии, населения и капиталовооруженности

При капиталовооруженности, соответствующей уровню «золотого правила», производственная функция f(к*) и линия dk* имеют одинаковый наклон и потребление достигает максимального уровня.

При уровне капиталовооруженности к** увеличение запаса капитала на единицу дает прирост выпуска, равный предельному продукту капитала МРК, и увеличивает выбытие капитала на величину d. Таким образом, при уровне капиталовооруженности к**, соответствующем «золотому правилу», выполняется условие MPK=d а с учетом роста населения и технического прогресса:

MPK=(d+n+g).

Если экономика развивается с запасом капитала, большим, чем она могла бы иметь по «золотому правилу», то в этом случае необходимо проводить политику, направленную на снижение нормы сбережений. Уменьшение нормы сбережения ведет к увеличению потребления и соответствующему снижению инвестиций, а значит, и уменьшению устойчивого уровня запаса капитала.

Если экономика начинает развиваться с меньшей капиталовооруженностью, чем при устойчивом состоянии по «золотому правилу», необходимо увеличить норму сбережений. Это повысит инвестиции и снизит потребление, но по мере накопления капитала с некоторого момента потребление снова начнет расти. В результате экономика достигнет нового равновесного состояния, но уже в соответствии с «золотым правилом», где потребление будет иметь более высокий уровень по сравнению с начальным.

План семинарского (практического)занятия

1) Определение экономического роста. Измерение экономического роста. Темпы экономического роста.

2) Факторы экономического роста. Типы экономического роста: экстенсивный и интенсивный. Факторы, сдерживающие экономический рост. Аргументы «за» и «против» экономического роста.

3) Модели экономического роста: кейнсианская и неоклассическая.

Вопросы для самоконтроля и проверки:

1) Что такое экономический рост и как его можно измерить?

2) Чем экономический рост отличается от экономического развития?

3) Что понимается под экономическим ростом и каковы его типы?

4) Какой тип экономического роста имеет место в России в настоящее время?

5) Чем был обусловлен экстенсивный тип экономического роста в СССР?

6) Какие показатели характеризуют экономическое развитие?

7) Каковы позитивные результаты экономической динамики?

8) Перечислите основные факторы экономического роста.

9) Какое воздействие оказывает использование НТП на факторы экономического роста?

10) Каковы причины экономических циклов?

11) Какие изменения происходят на различных фазах цикла?

12)Чем объясняется причина повторяемости кризисов недопроизводства товаров?

12)

Темы рефератов:

1) Особенности современного мирового экономического кризиса

2) Оценка реальных и потенциальных угроз кризиса для экономической безопасности России.

3) Прогнозные сценарии развития экономики России

Рекомендуемая литература:

1) Долан, Э.Дж. Economics Экономикс: англо-русский словарь-справочник / Э.Дж. Долан, Б.И. Домненко. - М.: Лазурь, 1994. - 544 c.

2) Липсиц, И.В. Микроэкономика. Макроэкономика: Учебник / И.В. Липсиц. - М.: КноРус, 2017. - 304 c.

3) Мэнкью, Н. Макроэкономика. / Н. Мэнкью. - СПб.: Питер, 2013. - 560 c.

4) Макконнелл Кэмпбелл, Брю Стенли. Экономикс: принципы, проблемы, политика. 18-е изд. — М.: ИНФРА-М. — 2011. — 1010 с.

5) Макроэкономика: теория и российская практика. Учебник для вузов. Под ред. А.Г.Грязновой, Н.Н.Думной. 2-е изд.-2005.- 688 с.

6) Самуэльсон. Экономика. Т. 1,2. — М.: НПО Алгон. — 1993.

7) Современная экономическая теория. /Под ред. Дж. Харвея. — М.: Юнити-Дана. — 2012. — 703 с.

8) Фишер Стенли и др. Экономика. — М.: Дело. — 2003. — 864 с.