Тепловые процессы при токарной обработке

Многочисленными исследованиями установлено, что температура оказывает доминирующее влияние на стойкость режущего инструмента.

Изнашивание передней поверхности резца в процессе точения происходит неравномерно и зависит от распределения температуры по этой поверхности. Так форма и размеры углубления на передней поверхности, образовавшегося вследствие изнашивания (лунки изнашивания), зависят от значения температуры, а координата этого углубления совпадает с координатой ее максимального значения. Таким образом, зная температурное поле режущего инструмента, можно прогнозировать интенсивность его изнашивания и период стойкости.

Исследовать температурное поле инструмента путем натурных экспериментов затруднительно, поэтому для этих целей широко используют моделирование.

В расчетах общей мощности тепловыделения при токарной обработке обычно принимают во внимание мощности тепловыделения источников, возникающих как результат перехода в теплоту работы деформирования и работы сил трения на передней и задней поверхностях инструмента. Практически все источники тепловыделения при резании являются трехмерными. Однако в большинстве случаев задачу упрощают и принимают эти источники двумерными, что не оказывает заметного влияния на точность расчетов [4.1].

Для источников тепловыделения, действующих в процессе механической обработки, вид зависимости, описывающей закон распределения плотности тепловыделения, достаточно сложен. При схематизации теплообмена на основе анализа параметров, определяющих тепловыделение (силы, коэффициенты трения, скорости), или на основе экспериментов получают представление о возможном законе распределения плотности тепловыделения и аппроксимируют его какой-либо функцией. Источник, возникающий на плоскости сдвига, принимают распределенным равномерно. Распределение сил трения и плотность теплового источника на поверхности контакта стружки с резцом описывают, как правило, комбинированным законом. Удовлетворительные результаты дает описание плотности этого источника несимметричным нормальным законом распределения.

На поверхности трения заготовки о заднюю поверхность резца действует тепловой источник, эквивалентный теплоте трения, и соответствующий тепловой поток принимают распределенным по несимметричному нормальному закону.

Теплота, выделяемая в зоне обработки, расходуется на нагревание инструмента, стружки, заготовки и окружающей среды. Тепловое состояние каждого из этих объектов характеризуется температурным полем, под которым понимают совокупность мгновенных значений температуры во всех точках тела [4.1, 4.2]. Температура Т в общем случае изменяется вдоль координатных осей х, у, z и с течением времени τ:

Т = f(x, y, z, τ).

Температурное поле, изменяющееся во времени, называют нестационарным, или неустановившимся; не изменяющееся во времени – стационарным, или установившимся. Стационарное поле можно описать следующей зависимостью:

Т = f(x, y, z).

В зависимости от того, в направлении скольких координатных осей изменяется температурное поле, различают одно-, двух- и трехмерные температурные поля.

Распределение температуры внутри тела описывается дифференциальным уравнением теплопроводности, которое применительно к нестационарному трехмерному температурному полю в декартовой системе координат имеет следующий вид:

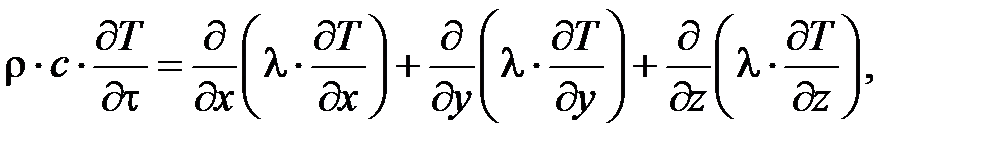
где ρ – плотность материала, кг/м³; с – удельная теплоемкость материала, Дж/(кг·К); τ – время, с.

Передача теплоты между движущейся средой и поверхностью какого-либо тела (твердого, жидкого, газообразного) осуществляется путем конвективного теплообмена и теплопроводности. При механической обработке это, например, теплообмен между заготовкой и смазочно-охлаждающей жидкостью (СОЖ), заготовкой и воздухом, инструментом и СОЖ, инструментом и воздухом, воздухом и СОЖ. Для расчета теплоотдачи используют формулу Ньютона-Рихмана:

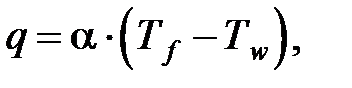
где α – коэффициент теплоотдачи, Вт/(м²·К); 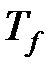, 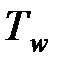– температура соответственно потока СОЖ и обтекаемой поверхности, К.

Математическая формулировка тепловой задачи должна содержать:

1) дифференциальное уравнение или систему уравнений (в зависимости от степени схематизации процесса) теплопроводности контактирующих твердых тел;

2) дифференциальное уравнение энергии СОЖ (при необходимости);

3) краевые условия или условия однозначности:

– геометрические, отражающие форму и размеры тел и их поверхностей, участвующих в теплообмене;

– физические, характеризующие физические свойства всех тел, участвующих в теплообмене;

– динамические, содержащие информацию о полях массовых сил (задают при необходимости);

– граничные, определяющие особенности протекания тепловых процессов на границах анализируемой системы;

– начальные, определяющие начальное состояние системы (задают только при анализе нестационарного теплообмена).

Граничные условия – обязательная часть постановки любой задачи теплообмена, правильность которых во многом определяет качество получаемого решения. Эти условия могут быть заданы в четырех различных вариантах:

1) граничные условия 1 рода задают распределение температуры на поверхностях тела, участвующего в теплообмене, и ее изменение во времени;

2) граничные условия 2 рода определяют распределение плотности теплового потока на поверхностях тела, участвующего в теплообмене, и ее изменение во времени;

3) граничные условия 3 рода устанавливают температуру сред, омывающих тело, и условия теплообмена (коэффициенты теплоотдачи) между средами и поверхностями тела, а также изменения этих параметров во времени;

4) граничные условия 4 рода задают равенство тепловых потоков и температур в зоне контакта двух тел.

Естественно, формулировка тепловой задачи может содержать комбинацию перечисленных граничных условий.

Точные аналитические методы решения задач теплопроводности часто связаны с трудностями, непреодолимыми при решении нелинейных задач. Нелинейные задачи возникают, в частности, если принимается во внимание зависимость теплофизических характеристик материалов контактирующих объектов (заготовки и инструмента) и механических характеристик материала заготовки от температуры. В таких случаях обращаются к численным методам решения.

Одним из широко используемых численных методов решения задач теплопроводности является метод конечных разностей [4.3]. Этот метод основан на замене производных дифференциальных уравнений их приближенными значениями, выраженными через разности значений функций в отдельных дискретных точках – узлах сетки. Дифференциальные уравнения заменяют эквивалентными соотношениями в конечных разностях.

Производную функции, описываемой кривой AP (рис. 4.1), можно выразить через угол α_i наклона касательной к этой кривой:

.

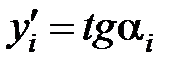Если разности 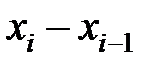; 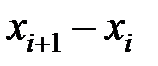достаточно малы, т. е. не превышают значения, при котором обеспечивается «устойчивость» решения [4.3], то угол α_i можно заменить на углы β_i и γ_i (см. рис. 4.1) и получить следующие разностные выражения:

;

;

.

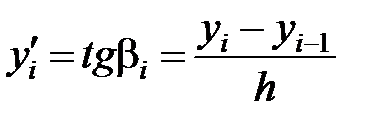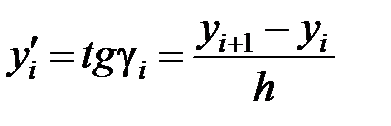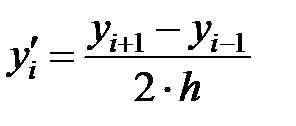Приближенное значение второй производной:

.

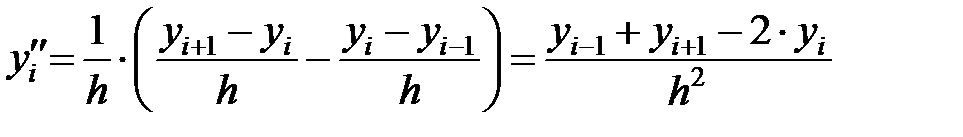Уравнение теплопроводности, описывающее нестационарное одномерное температурное поле, имеет следующий вид:

.

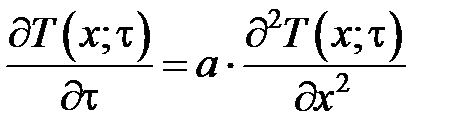Поскольку температура T зависит от двух переменных – времени τ и координаты x, для получения приближенных значений производных следует использовать сетку прямоугольного типа.

На схеме, показанной на рис. 4.2, по оси абсцисс отложена координата x, вдоль которой распространяется температура, а по оси ординат – время τ. Через h и Δτ обозначены соответственно размер элементов, на которые мысленно разбит анализируемый объект, и конечный малый промежуток времени, на которые разбито время τ_т, в течение которого происходит теплообмен.

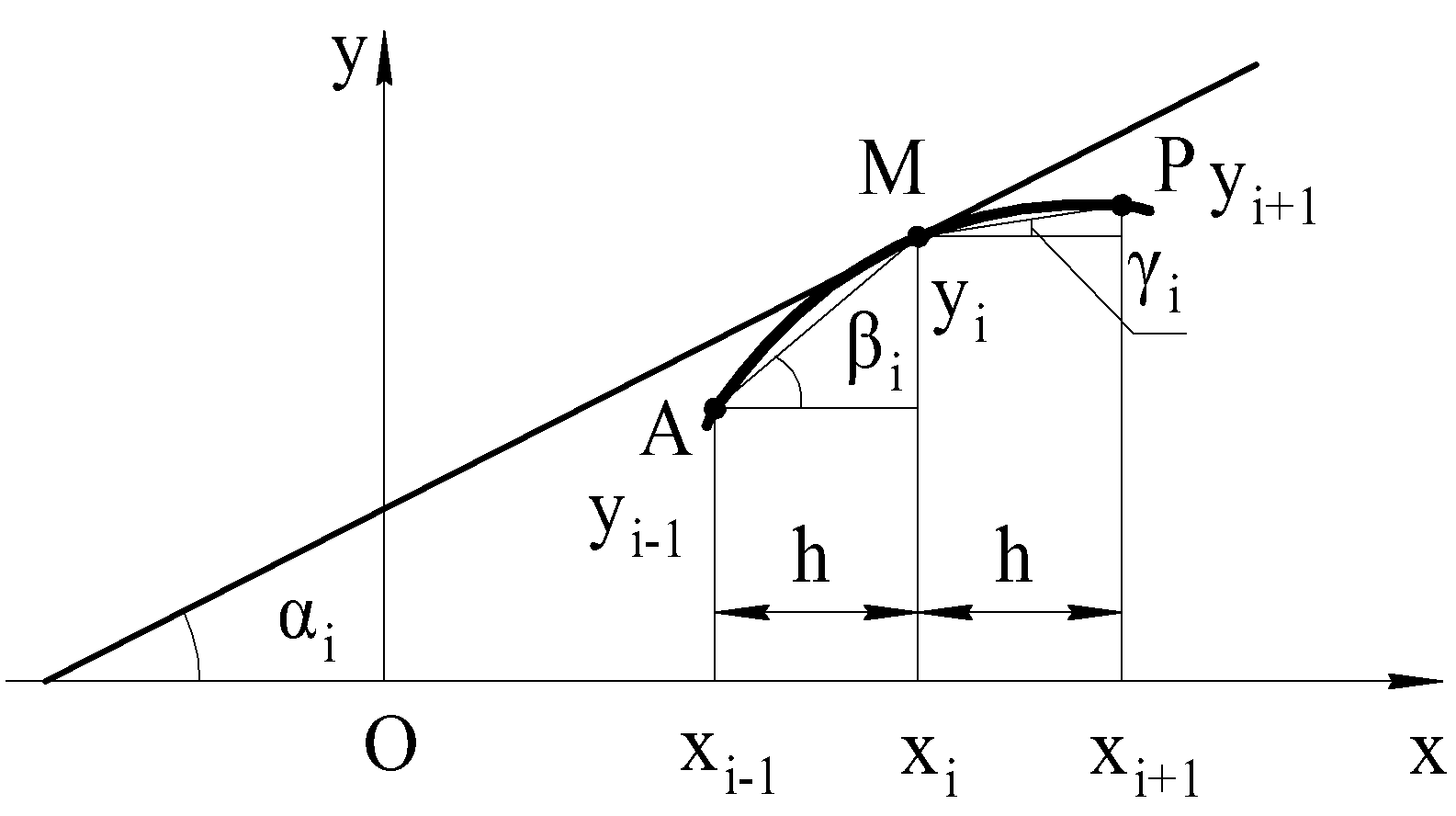
Рис. 4.1. Схема для вывода разностных выражений

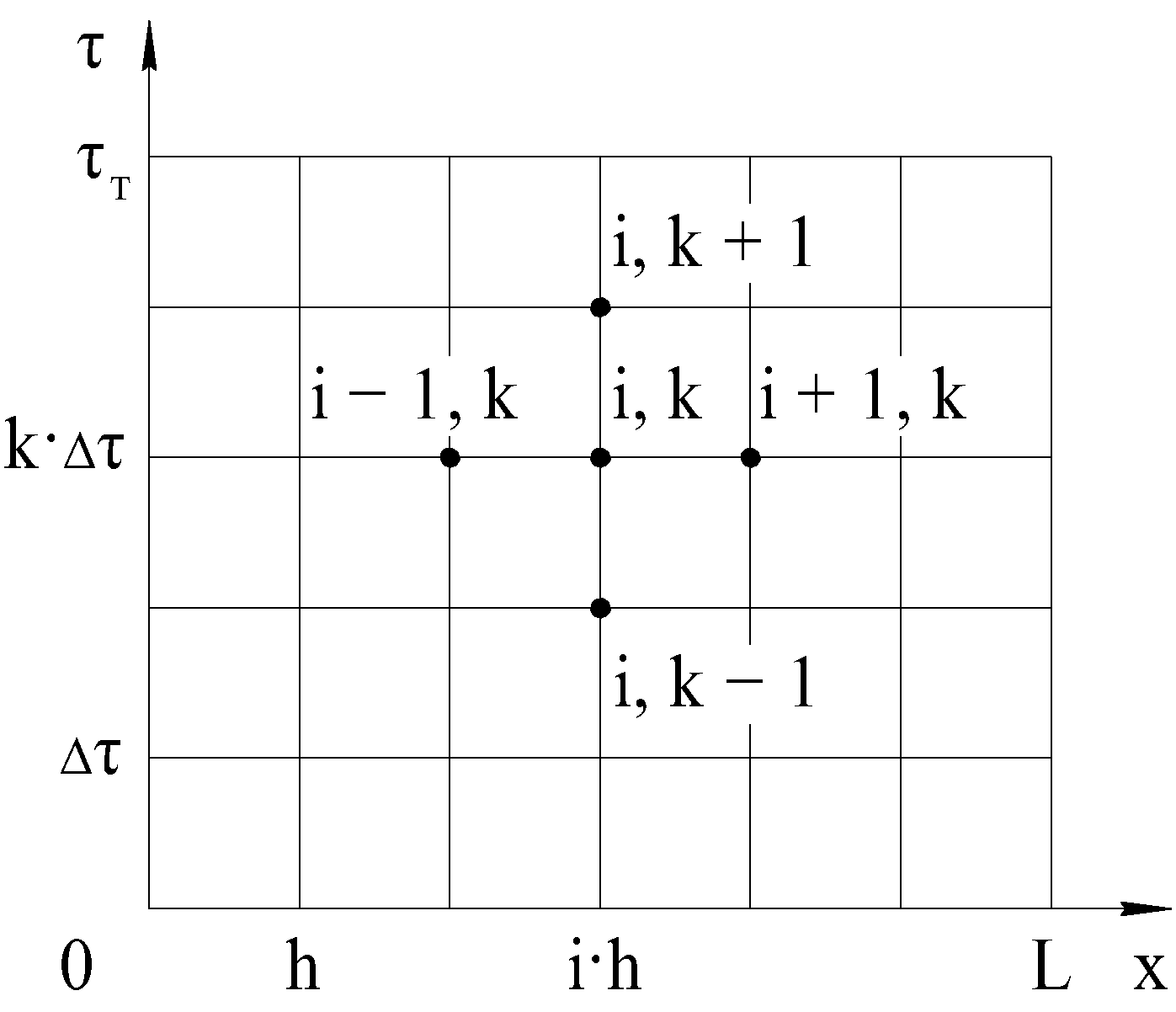
Рис. 4.2. Схема для вывода разностного уравнения теплопроводности

Выразим частные производные ∂Т/∂τ, ∂²Т/∂x² в точке i, k через разностные отношения:

;

.

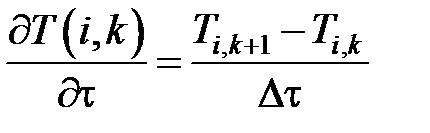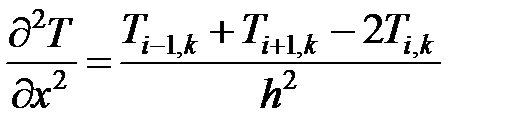Использовав эти отношения, получим разностное уравнение

,

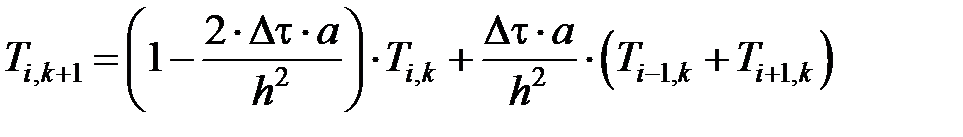которое позволяет вычислить значение температуры в точке с координатами i, k + 1(вмомент времени τ = k +1) по значениям температур в точке с координатами i, k и в соседних с ней точках с координатами i – 1, i + 1 в предыдущий момент времени τ = k. Значения температур в начальный момент времени τ = 0 известны из начальных условий; температуры в точках с координатами x = 0 и x = L, где L – размер рассматриваемого объекта, известны из граничных условий 1 рода.

Таким образом, получается система алгебраических уравнений, которые составляют алгоритм численного интегрирования нестационарного уравнения теплопроводности. Такая математическая модель является базой прикладной программы «Тепло» [4.4], предназначенной для исследования температурного поля в режущем клине инструмента при точении.

Программа позволяет рассчитывать температурное поле в зависимости от различных параметров процесса обработки: материалов заготовки и инструмента (резца), переднего, заднего и главного угла в плане, глубины резания, подачи, скорости резания и диаметра заготовки.