Математические модели, зависимости и методики расчета температур при точении
Температуры на рабочих поверхностях режущего инструмента (передней и задней) и на обрабатываемых поверхностях заготовки оказывают существенное влияние на работоспособность инструмента, качество обработанных поверхностей и производительность обработки. Без знания этих температур невозможно решить многие задачи, возникающие при проектировании технологических операций, в том числе назначить рациональные условия и режим обработки.
При теплофизическом анализе полагают, что теплота при точении выделяется в области стружкообразования и на поверхностях контакта резца со стружкой и заготовкой (рис. 3.1). Если два последних источника являются плоскими, то источник теплоты в области стружкообразования является объемным. Однако этот источник также считают плоским, причем это допущение не вносит заметных погрешностей в результаты расчета.
Общая мощность тепловыделения при резании:
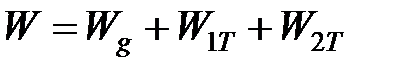 ,
,
где 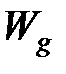 ,
, 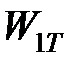 ,
, 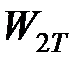 – мощности тепловыделения источников, возникающих как результат перехода в теплоту работы деформирования
– мощности тепловыделения источников, возникающих как результат перехода в теплоту работы деформирования 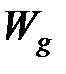 , работы сил трения на передней
, работы сил трения на передней 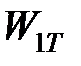 и задней
и задней 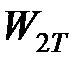 поверхностях режущего клина, Вт.
поверхностях режущего клина, Вт.
Мощности источников можно определить как [3.1]
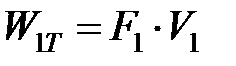 ;
; 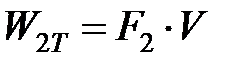 ;
; 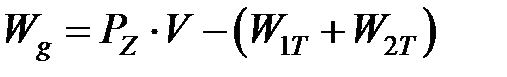 , (3.1)
, (3.1)
где 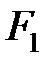 и
и 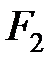 – силы трения на поверхности контакта резца со стружкой и заготовкой соответственно, Н; V – скорость резания, м/с; V1 – скорость перемещения стружки относительно резца, м/с:
– силы трения на поверхности контакта резца со стружкой и заготовкой соответственно, Н; V – скорость резания, м/с; V1 – скорость перемещения стружки относительно резца, м/с: 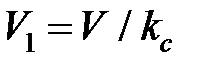 , где
, где 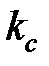 – коэффициент утолщения стружки;
– коэффициент утолщения стружки; 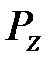 – главная составляющая силы резания, Н.
– главная составляющая силы резания, Н.
Согласно работе [3.5],
 ; (3.2)
; (3.2)
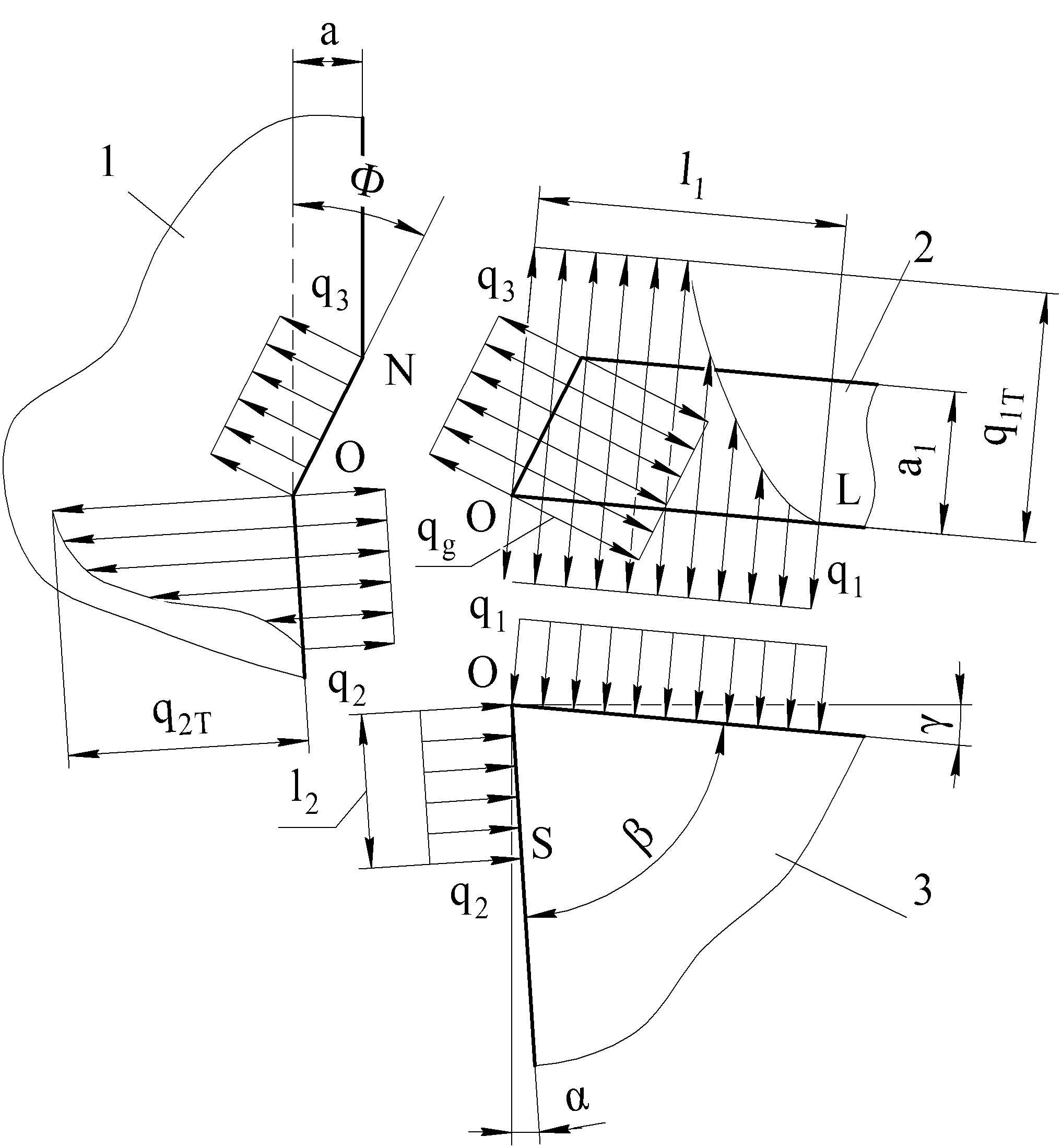
Рис. 3.1. Структурная схема теплообмена в зоне резания:
1 – заготовка; 2 – стружка; 3 – инструмент
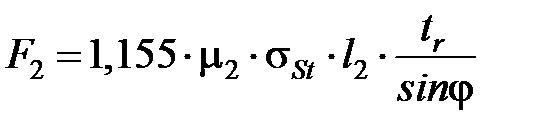 , (3.3)
, (3.3)
где 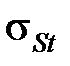 – среднее по области пластической деформации напряжение текучести обрабатываемого материала, соответствующее средней температуре в этой области, Па;
– среднее по области пластической деформации напряжение текучести обрабатываемого материала, соответствующее средней температуре в этой области, Па; 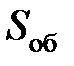 – подача на оборот заготовки, м/об;
– подача на оборот заготовки, м/об; 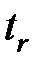 – глубина резания, м;
– глубина резания, м; 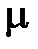 – коэффициент трения по напряжению текучести (
– коэффициент трения по напряжению текучести ( 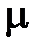 = 0,5 и
= 0,5 и  = 0,3 при отсутствии и наличии СОТС в зоне контакта соответственно);
= 0,3 при отсутствии и наличии СОТС в зоне контакта соответственно); 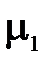 ,
, 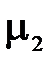 – коэффициент трения стружки о переднюю поверхность резца и задней поверхности резца о заготовку; γ – передний угол резца, град.;
– коэффициент трения стружки о переднюю поверхность резца и задней поверхности резца о заготовку; γ – передний угол резца, град.; 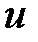 – коэффициент, принимающий значения:
– коэффициент, принимающий значения:
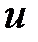 = 1 при γ ≥ 0;
= 1 при γ ≥ 0;
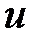 = 1 – sinγ при γ < 0;
= 1 – sinγ при γ < 0;
 – главный угол резца в плане, град.;
– главный угол резца в плане, град.;  – длина контакта задней поверхности резца с заготовкой, м.
– длина контакта задней поверхности резца с заготовкой, м.
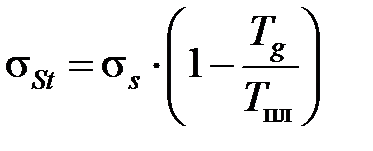 , (3.4)
, (3.4)
где 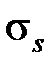 – напряжения текучести при температуре 20 °С, Па;
– напряжения текучести при температуре 20 °С, Па; 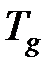 – температура в области пластической деформации, °С;
– температура в области пластической деформации, °С; 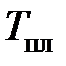 – температура плавления обрабатываемого материала, °С.
– температура плавления обрабатываемого материала, °С.
При работе резцом без площадки износа
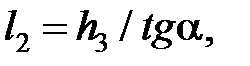
где 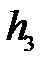 – высота упругого поднятия металла в зоне задней поверхности резца, м;
– высота упругого поднятия металла в зоне задней поверхности резца, м; 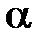 – задний угол резца, град.
– задний угол резца, град.
Параметр 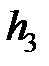 можно определить как [3.6]
можно определить как [3.6]
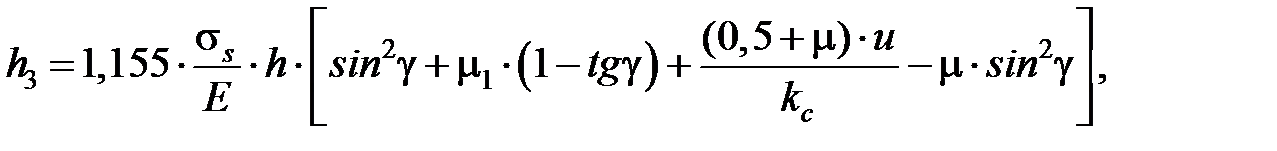 (3.5)
(3.5)
где 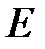 – модуль упругости материала обрабатываемой заготовки, Па; h – размер заготовки (при токарной обработке h = d/2, где d – диаметр обработанной заготовки, м).
– модуль упругости материала обрабатываемой заготовки, Па; h – размер заготовки (при токарной обработке h = d/2, где d – диаметр обработанной заготовки, м).
При работе резцом с площадкой затупления
 (3.6)
(3.6)
где lи – размер площадки износа, связанный с радиальным износом hu зависимостью [3.7]:
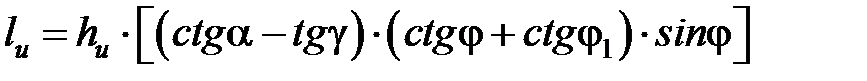 , (3.7)
, (3.7)
где 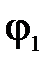 – вспомогательный угол в плане, град.
– вспомогательный угол в плане, град.
Для расчета 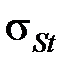 необходимо знать температуру
необходимо знать температуру  [3.4] в области пластической деформации:
[3.4] в области пластической деформации:
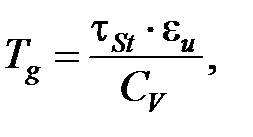 (3.8)
(3.8)
где 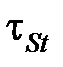 – средние касательные напряжения в условной поверхности сдвига, Па;
– средние касательные напряжения в условной поверхности сдвига, Па; 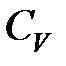 – удельная объемная теплоемкость, Дж/(м3·К);
– удельная объемная теплоемкость, Дж/(м3·К); 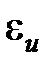 – истинный сдвиг, определяемый по следующей зависимости [3.4]:
– истинный сдвиг, определяемый по следующей зависимости [3.4]:
 . (3.9)
. (3.9)
Учитывая, что параметр 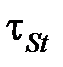 связан с напряжением текучести
связан с напряжением текучести 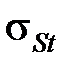 зависимостью
зависимостью
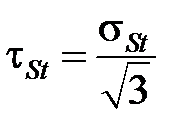 , (3.10)
, (3.10)
зависимость для расчета 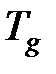 можно представить в следующем виде:
можно представить в следующем виде:
 .
.
Для расчета  следует использовать метод последовательных приближений: задавшись температурой
следует использовать метод последовательных приближений: задавшись температурой 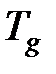 , определить
, определить 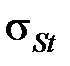 , затем рассчитать
, затем рассчитать  ; уточнить
; уточнить  и вновь определить
и вновь определить 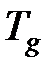 . Итерации продолжать до получения расхождения между полученными последовательно значениями
. Итерации продолжать до получения расхождения между полученными последовательно значениями 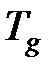 менее 5 %.
менее 5 %.
Расчет главной составляющей силы резания можно выполнить по зависимости [3.5]
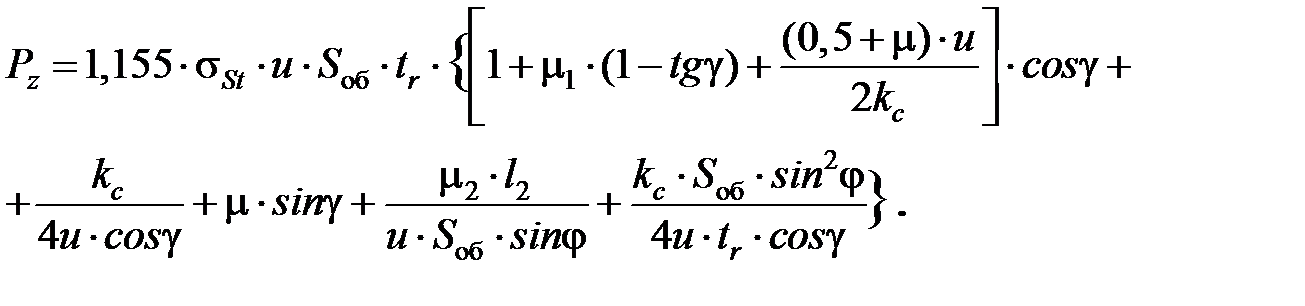 (3.11)
(3.11)
Полагаем, что источник плотностью 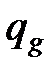 , возникающий на плоскости сдвига, распределен равномерно:
, возникающий на плоскости сдвига, распределен равномерно:
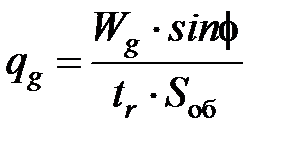 , (3.12)
, (3.12)
где 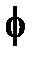 – угол сдвига:
– угол сдвига:
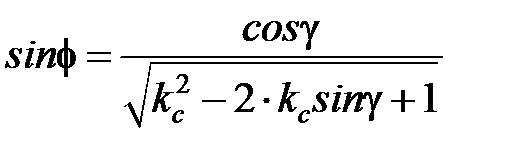 . (3.13)
. (3.13)
При комбинированном законе распределения теплового источника на поверхности контакта стружки с передней поверхностью инструмента его плотность
 , (3.14)
, (3.14)
где 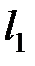 – длина контакта стружки с инструментом, которую можно определить по зависимости Н. Г. Абуладзе [3.7]:
– длина контакта стружки с инструментом, которую можно определить по зависимости Н. Г. Абуладзе [3.7]:
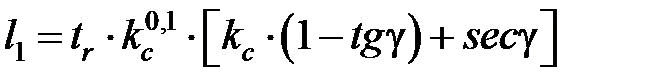 . (3.15)
. (3.15)
При несимметричном нормальном распределении источника на поверхности контакта резца с заготовкой максимальная плотность потока [3.1]
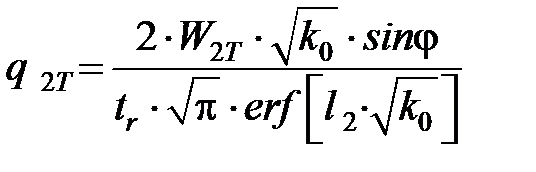 , (3.16)
, (3.16)
где 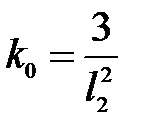 – коэффициент; erf – функция, называемая интегралом вероятности:
– коэффициент; erf – функция, называемая интегралом вероятности:
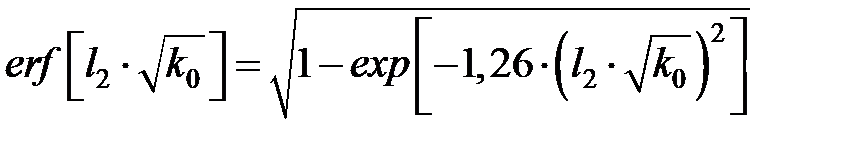 , (3.17)
, (3.17)
или
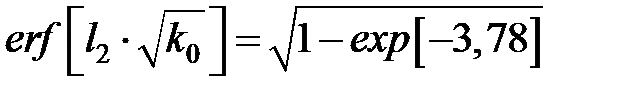 .
.
Для расчета плотности тепловых источников можно использовать иные зависимости, например [3.3]:
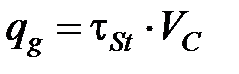 , (3.18)
, (3.18)
где 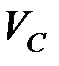 – скорость сдвига, м/с:
– скорость сдвига, м/с:
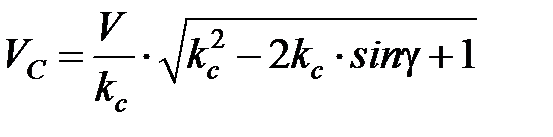 , (3.19)
, (3.19)
где  – скорость резания, м/с.
– скорость резания, м/с.
Плотность теплового потока от трения стружки по передней поверхности при равномерном распределении теплового источника
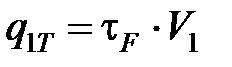 , (3.20)
, (3.20)
где 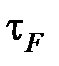 – среднее касательное напряжение на передней поверхности, Па [3.3]:
– среднее касательное напряжение на передней поверхности, Па [3.3]:
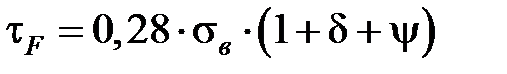 ,
,
где 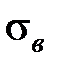 – предел прочности при растяжении материала заготовки, Па;
– предел прочности при растяжении материала заготовки, Па; 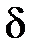 и
и 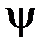 – относительное удлинение и сужение при стандартном испытании образца из материала обрабатываемой заготовки.
– относительное удлинение и сужение при стандартном испытании образца из материала обрабатываемой заготовки.
Если интенсивность источника теплоты 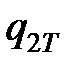 принять равномерной, то плотность теплового потока
принять равномерной, то плотность теплового потока
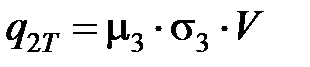 , (3.21)
, (3.21)
где 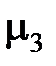 – коэффициент трения задней поверхности инструмента о заготовку;
– коэффициент трения задней поверхности инструмента о заготовку; 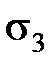 – среднее нормальное напряжение; для пластичных материалов
– среднее нормальное напряжение; для пластичных материалов
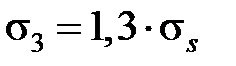 .
.
Суть инженерной методики расчета температур на площадках контактирующих при резании объектов, предложенной А. Н. Резниковым [3.1, 3.2], заключается в том, что формулы для расчета температуры представляют в виде ряда сомножителей, причем структура этих формул соответствует структуре кодов, служащих для описания тепловых задач.
Кодированная запись тепловой задачи для каждого источника или стока теплоты состоит из трех групп символов и имеет вид
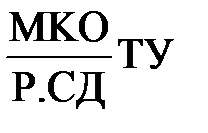 .
.
Первая группа символов (табл. 3.1) содержит информацию о мерности (М), конфигурации зоны тепловыделения (К) и ограниченности (О) источника. Вторая группа указывает на законы распределения плотности тепловыделения по осям координат (Р), скорость движения источника (С) и длительность его функционирования (Д). Третья группа содержит информацию о форме объекта (Т), на который действует источник, и род граничных условий (У).
3.1. Значения (коды) символов при кодировании тепловых задач [3.1]
| Символ | Признак источника и тела | Коды |
| М | Точечный Одно-, двух- и трехмерный | 1; 2; 3 |
| К | Прямой, плоский (полосовой, прямоугольный), призматический Кольцевой, круговой, цилиндрический Шаровой | |
| О | Неограниченный Ограниченный по направлению одной, двух или трех осей координат | 1; 2; 3 |
| Р | Распределенный равномерно Распределенный линейно Распределенный по экспоненте Нормально распределенный несимметричный Нормально распределенный симметричный Комбинированный | 2; 3 5; 6 |
| С | Неподвижный Движущийся Быстродвижущийся | |
| Д | Мгновенный Действующий некоторое время Действующий длительно (процесс установился) | |
| Т | Неограниченное тело Полупространство Пластина Параллелепипед Стержень неограниченный Стержень, ограниченный с одной стороны Стержень конечной длины Цилиндр Клин Шар | |
| У | Граничные условия 1, 2, 3, 4 рода | 1; 2; 3; 4 |
Каждому из символов соответствует одна цифра, кроме символа Р, который содержит 3 цифры, указывающие на распределение плотности тепловыделения по трем осям координат (см. табл. 3.1).
В соответствии с этими символами формула для расчета температур имеет следующий вид:
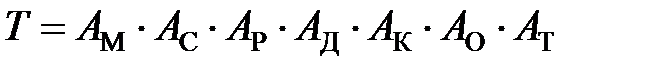 ; (3.22)
; (3.22)
в этой формуле значение каждого из сомножителей «А» зависит от значения соответствующего символа в коде тепловой задачи.
Сомножители имеют обозначение Аср, если рассчитывают среднюю температуру, и Аmax, если определяют максимальную температуру.
Для двумерного источника (М = 2), который наиболее часто встречается при теплофизическом анализе технологических процессов механической обработки, в качестве первого сомножителя принята величина АM = l/λ, где l – характерный размер источника (для подвижных источников – размер по направлению движения); λ – коэффициент теплопроводности объекта, Вт/(м·°С).
Для быстродвижущихся источников (С = 2) сомножитель 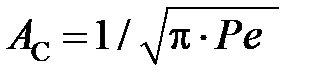 , где
, где 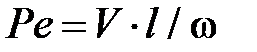 – критерий Пекле
– критерий Пекле 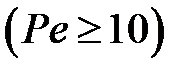 ;
;  – коэффициент температуропроводности объекта, м2/с. Для неподвижных источников (С = 0) коэффициент
– коэффициент температуропроводности объекта, м2/с. Для неподвижных источников (С = 0) коэффициент 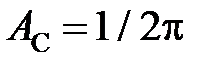 .
.
Коэффициент 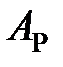 выбирают в зависимости от значений символов Р и С по табл. 3.2.
выбирают в зависимости от значений символов Р и С по табл. 3.2.
Коэффициент  для установившегося теплообмена (
для установившегося теплообмена ( 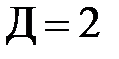 ), а также для быстродвижущихся источников, имеет значение
), а также для быстродвижущихся источников, имеет значение 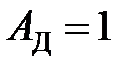 .
.
Если площадка имеет вид бесконечной полосы или прямоугольника (К = 1), то АК = 1.
Если источник тепловыделения имеет вид неограниченной полосы (О = 1) или круга, то АО = 1. Для прямоугольных источников, ограниченных в двух направлениях (О = 2), значения АО зависят от безразмерной величины 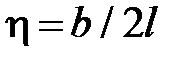 , где
, где  – ширина источника. Для неподвижных (С = 0) и быстродвижущихся источников (С = 2) значения АО приведены на рис. 3.2 в зависимости от значений безразмерного комплекса
– ширина источника. Для неподвижных (С = 0) и быстродвижущихся источников (С = 2) значения АО приведены на рис. 3.2 в зависимости от значений безразмерного комплекса 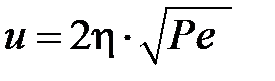 .
.
3.2. Коэффициент Ар в формуле (3.22) [3.1]
| Закон распределения (символ Р) | Арср | Арmax | Арср | Арmax |
| С = 0 | С = 2 | |||
| 3,06 1,53 1,53 1,49 1,49 2,70 – | 3,31 1,76 1,76 1,86 1,86 3,00 – | 0,67 0,40 0,27 0,36 0,20 0,29 0,51 | 1,00 0,47 0,67 0,44 0,54 0,49 0,71 |
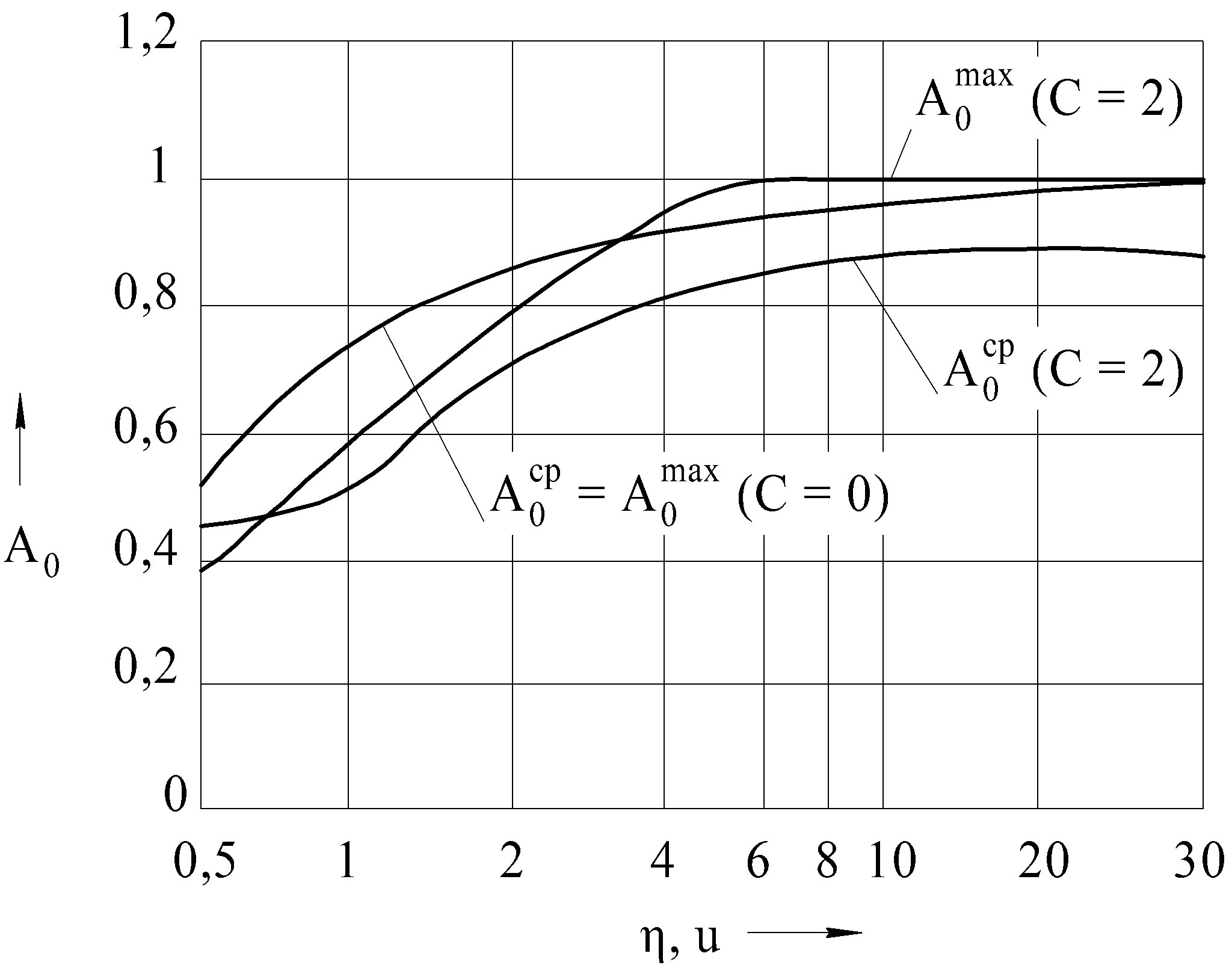
Рис. 3.2. Значения коэффициента АО в зависимости от безразмерной величины η (для неподвижных источников С = 0) и безразмерного комплекса u (для быстродвижущихся источников С = 2) [3.1]
 |
Для неограниченного объекта (Т = 0) коэффициент 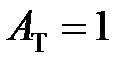 , для полубесконечного тела (Т = 1) с адиабатической границей
, для полубесконечного тела (Т = 1) с адиабатической границей 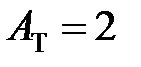 . В других случаях (Т > 1) коэффициент
. В других случаях (Т > 1) коэффициент 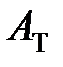 выбирают по табл. 3.3.
выбирают по табл. 3.3.
3.3. Коэффициенты АТ в формуле (3.22) [3.1]
| Символы | Диапазон значений | Атср | Атmax | |
| С | Т | |||
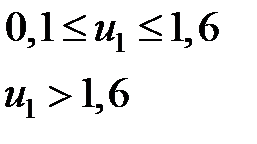
| 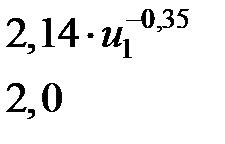
| 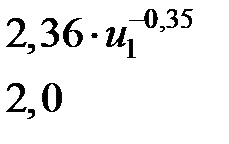
| ||
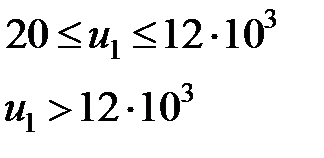
| 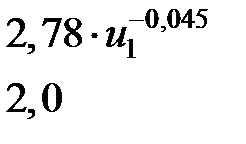
| 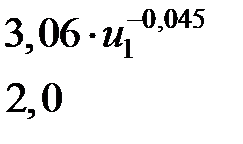
| ||
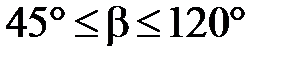
| 
|
Формулы для расчета температур на поверхностях контактирующих объектов записываются на основании кода задачи.
Температура на поверхности сдвига ON (см. рис. 3.1) со стороны заготовки
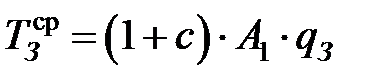 , (3.23)
, (3.23)
со стороны стружки
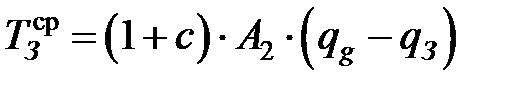 , (3.24)
, (3.24)
где 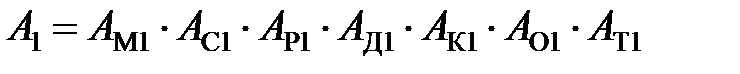 .
.
По аналогичной зависимости определяют коэффициенты 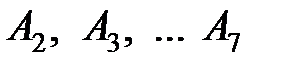 . Коэффициент с = 0,1.
. Коэффициент с = 0,1.
Выражения для расчета температур контактных площадок OL и OS со стороны стружки и заготовки имеют следующий вид:
 ; (3.25)
; (3.25)
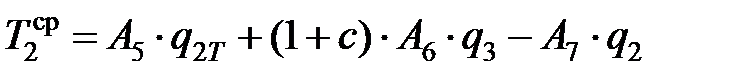 , (3.26)
, (3.26)
где А6 – коэффициент, учитывающий влияние источника плотностью q3 на температуру площадки OS: 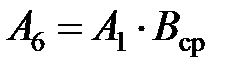 .
.
Параметр Вср можно определить как
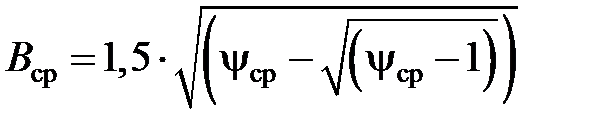 ,
,
где 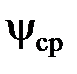 = 0,5·(ψ1 + ψ2) – безразмерная координата средней точки рассматриваемой площадки.
= 0,5·(ψ1 + ψ2) – безразмерная координата средней точки рассматриваемой площадки.
Безразмерные координаты ψ1 и ψ2 определяют по зависимостям:
ψ1 = L/L1; ψ2 = (L1+ L2)/L1,
где L – расстояние между источниками, м; L1 и L2 – размеры перемещающихся друг за другом источников, м (теплота, внесенная источником размером L1, влияет на температуру площадки размером L2).
Температуры контактных площадок OL и OS со стороны резца:
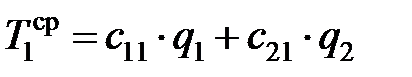 ; (3.27)
; (3.27)
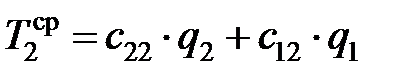 . (3.28)
. (3.28)
Первые слагаемые зависимостей (3.27) и (3.28) учитывают влияние источника теплоты, расположенного на данной поверхности, на температуру контактной площадки этой же поверхности. Вторые слагаемые учитывают, что источник, прогревая режущий клин, влияет на температуру контактной площадки, расположенной на противоположной поверхности. Так коэффициент с21 учитывает влияние источника 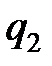 на температуру площадки OL.
на температуру площадки OL.
Коэффициенты 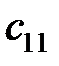 и
и 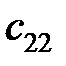 определяют аналогично коэффициентам
определяют аналогично коэффициентам 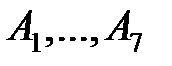 . Коэффициенты
. Коэффициенты 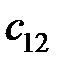 и
и 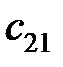 можно определить по следующим выражениям:
можно определить по следующим выражениям:
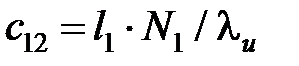 ; (3.29)
; (3.29)
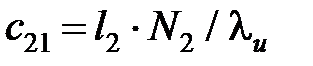 , (3.30)
, (3.30)
где 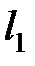 и
и 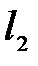 – длины контактных площадок, м (см. рис. 3.1);
– длины контактных площадок, м (см. рис. 3.1); 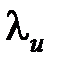 – коэффициент теплопроводности материала режущей части инструмента, Вт/(м ·°С).
– коэффициент теплопроводности материала режущей части инструмента, Вт/(м ·°С).
Параметры  и
и 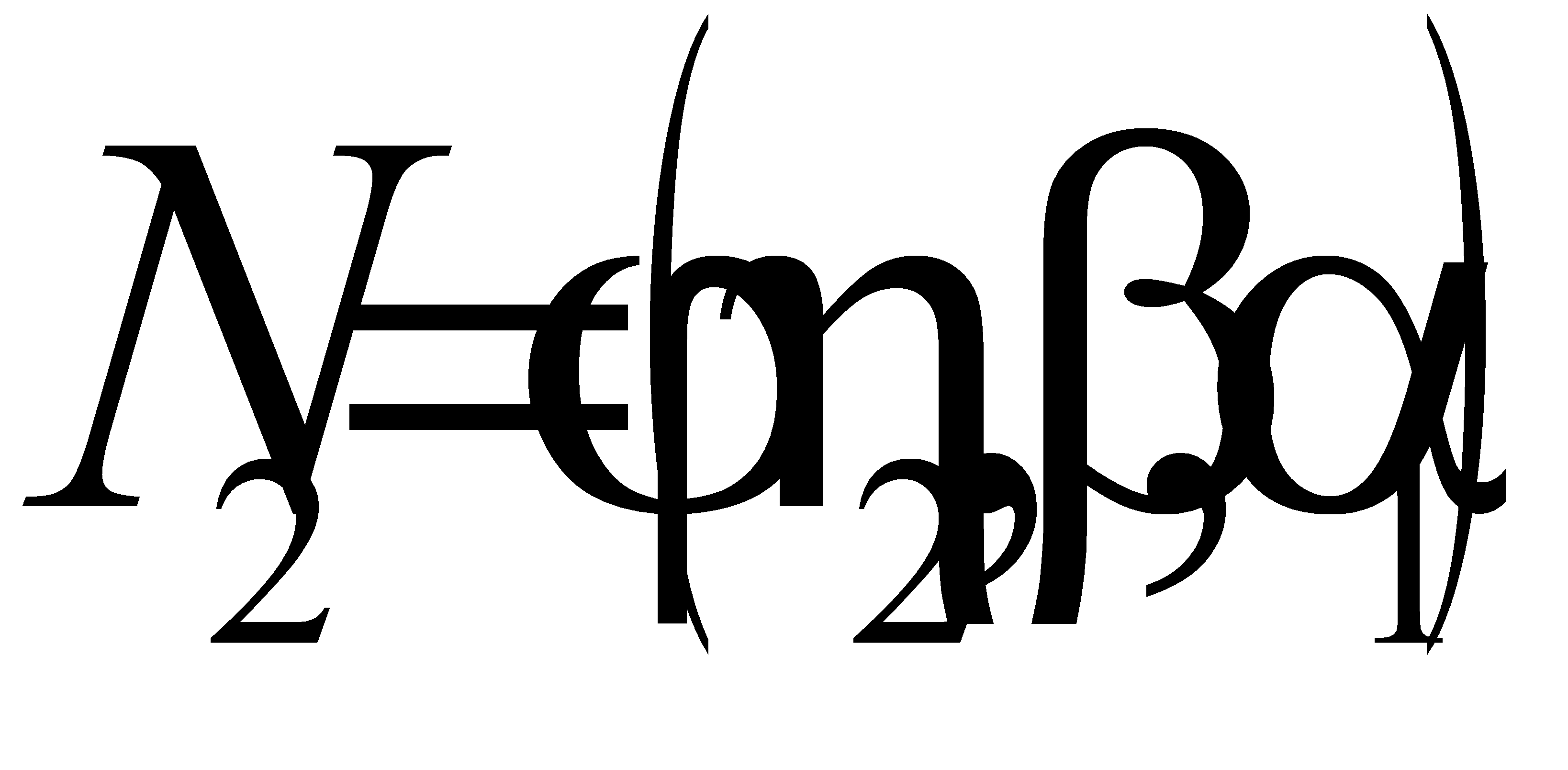 определяют по номограмме, приведенной на рис. 3.3. Их значения зависят от угла заострения режущего клина инструмента
определяют по номограмме, приведенной на рис. 3.3. Их значения зависят от угла заострения режущего клина инструмента 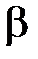 , безразмерной ширины площадок
, безразмерной ширины площадок 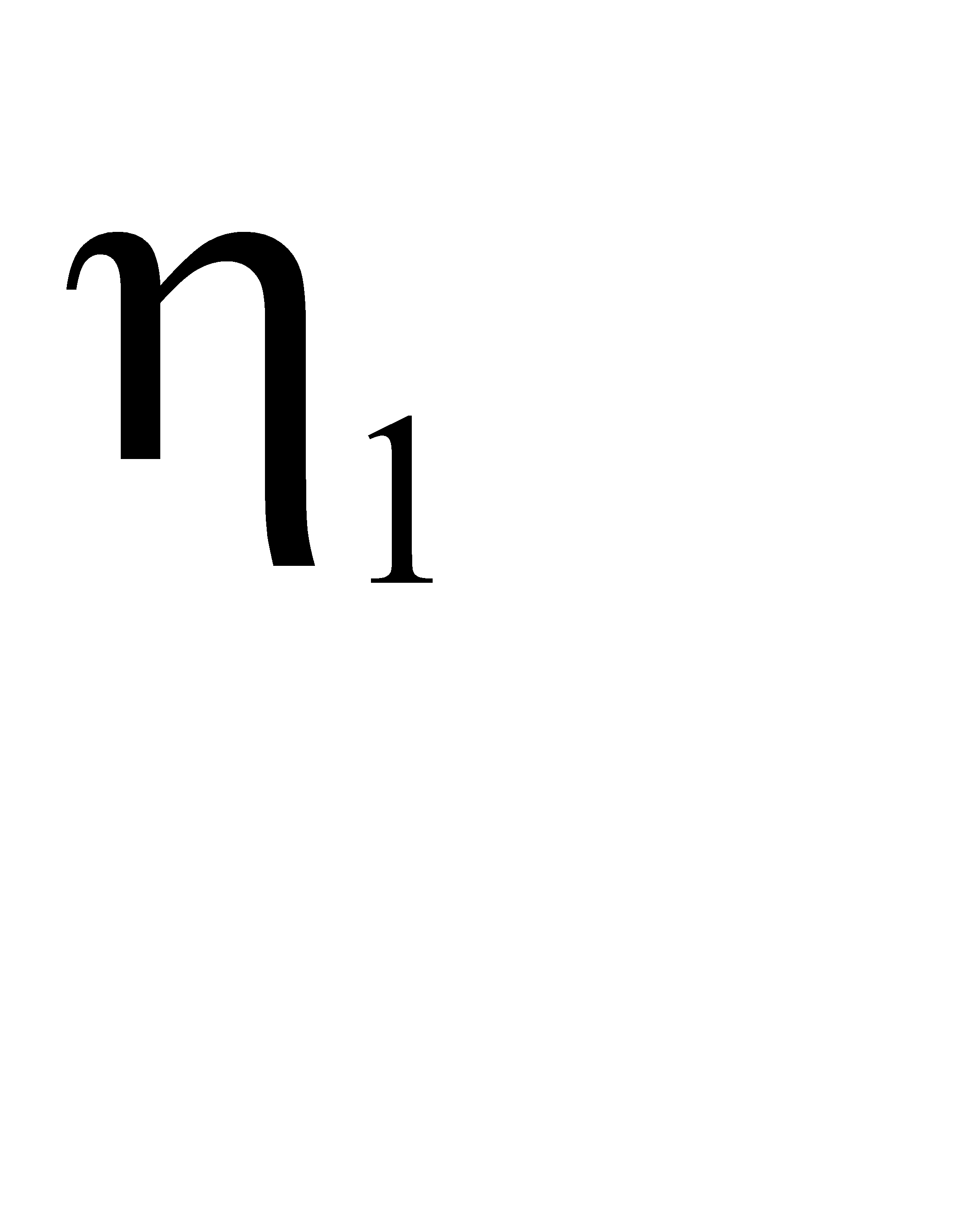 и
и 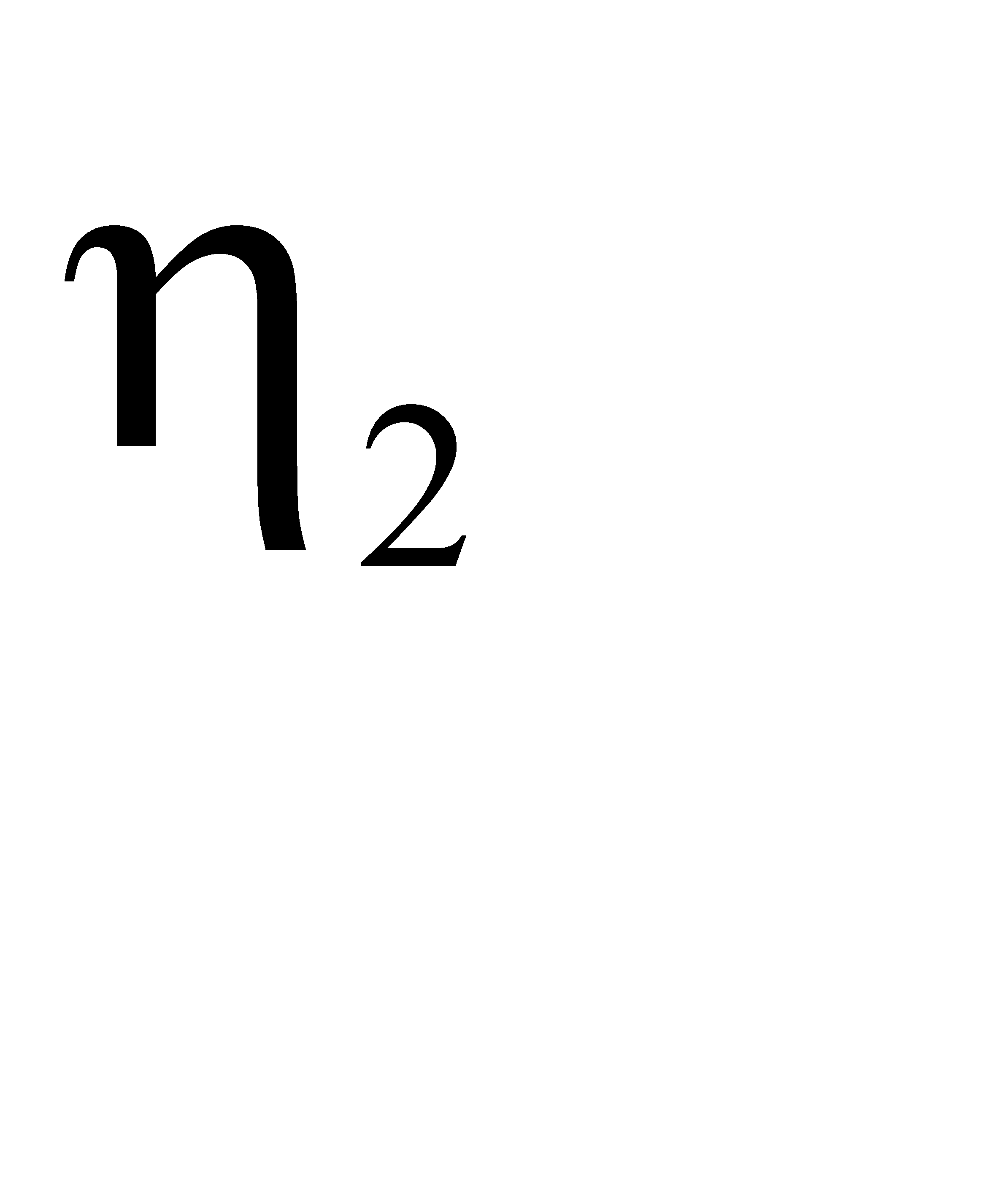 , а также соотношений
, а также соотношений 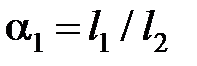 и
и 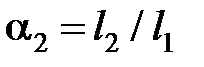 между длинами площадок.
между длинами площадок.
Параметры 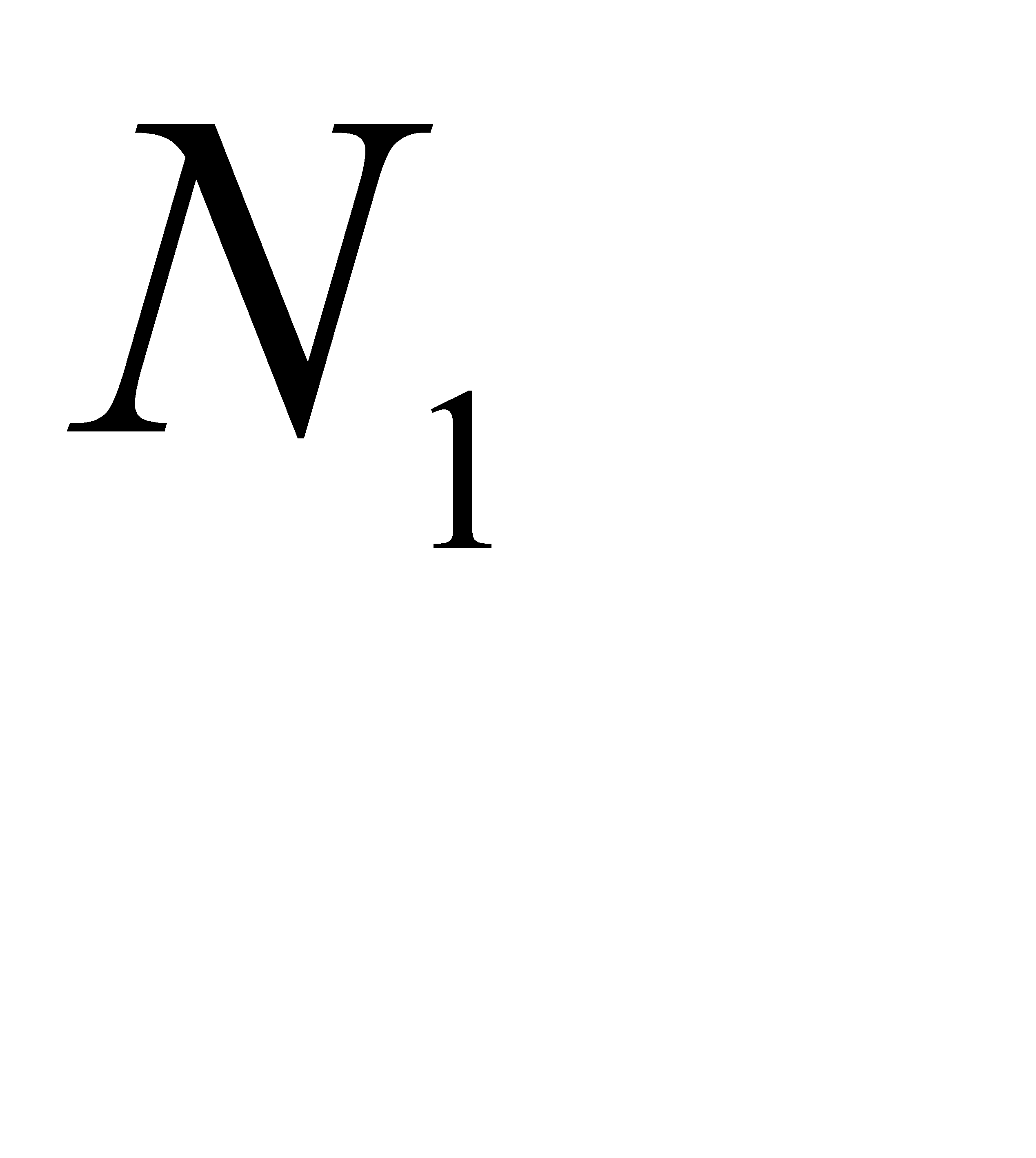 и
и 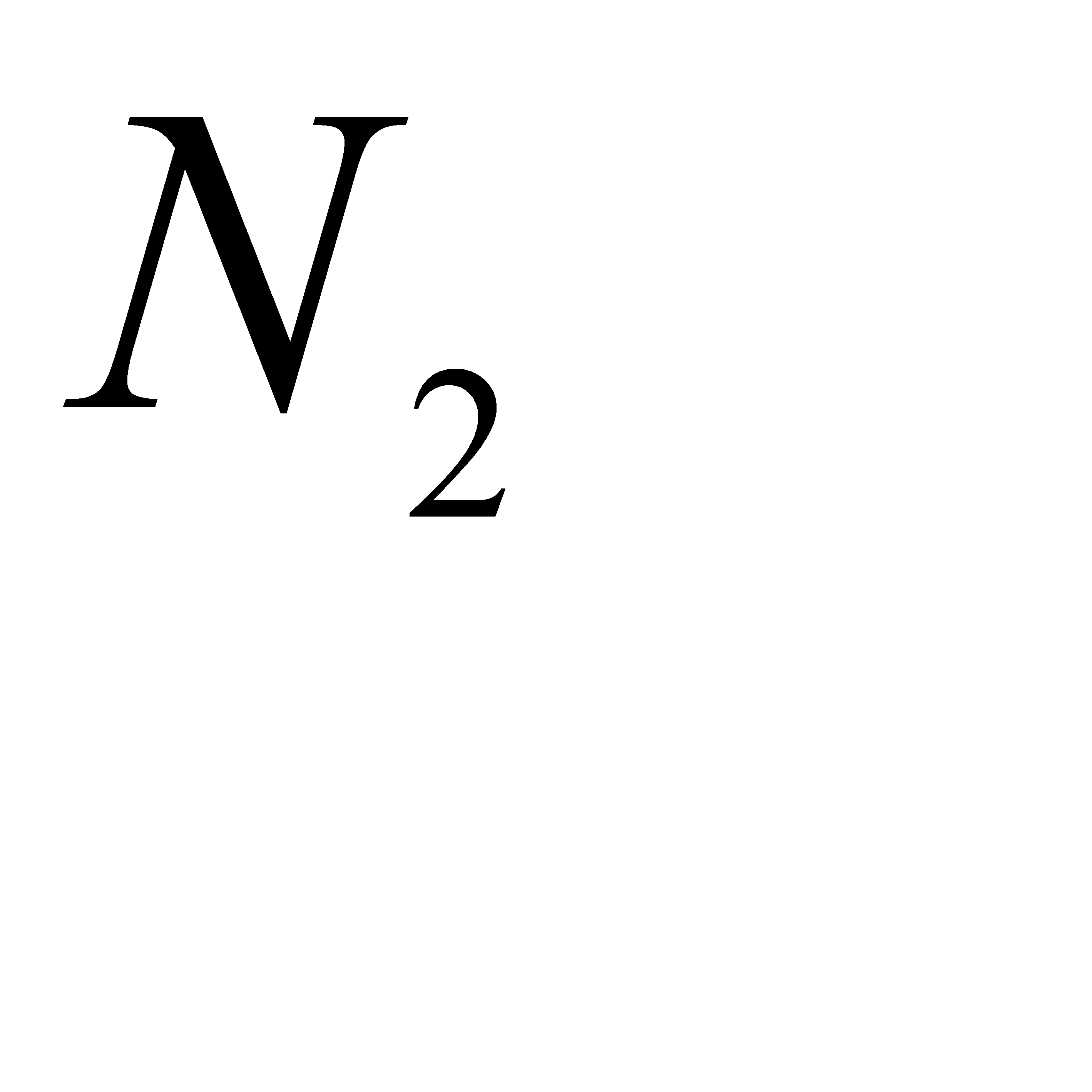 можно также определить по зависимостям
можно также определить по зависимостям
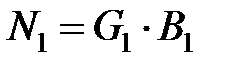 ;
; 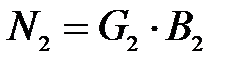 . (3.31)
. (3.31)
Значения функций G1 и G2 приведены в табл. 3.4.
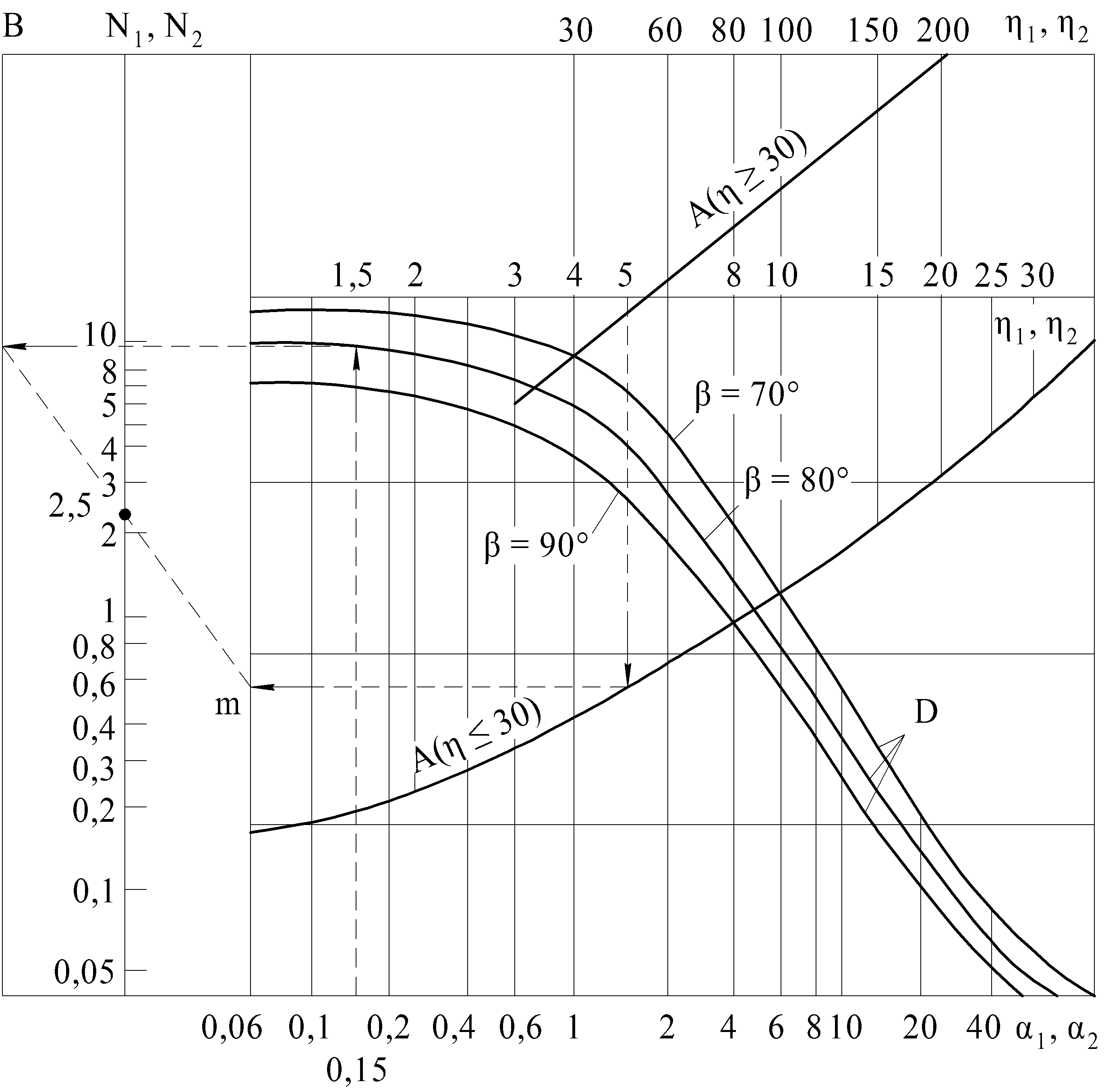
Рис. 3.3. Номограмма для определения параметров N1 и N2 [3.1]
Функции 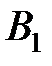 и
и 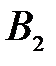 определяют по табл. 3.5 в зависимости от угла заострения
определяют по табл. 3.5 в зависимости от угла заострения 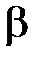 , соотношения параметров
, соотношения параметров 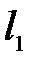 и
и 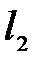 (
( 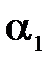 и
и 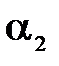 ).
).
Сопоставив попарно зависимости для расчета средних температур на контактных площадках, получим систему уравнений, в результате расчета которых можно определить плотности итоговых потоков q1 – q3.
3.4. Значения функций G1 и G2 [3.2]
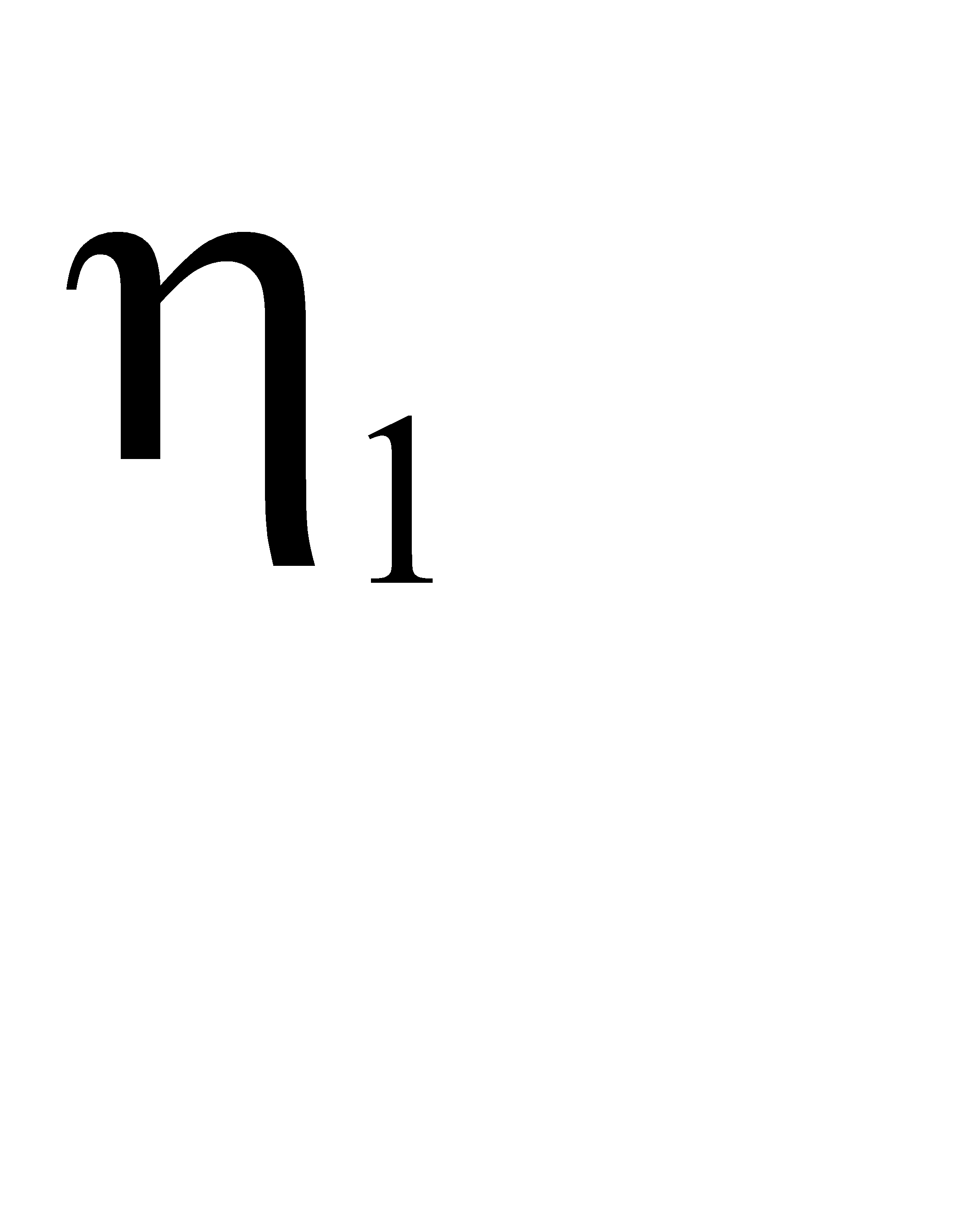 , , 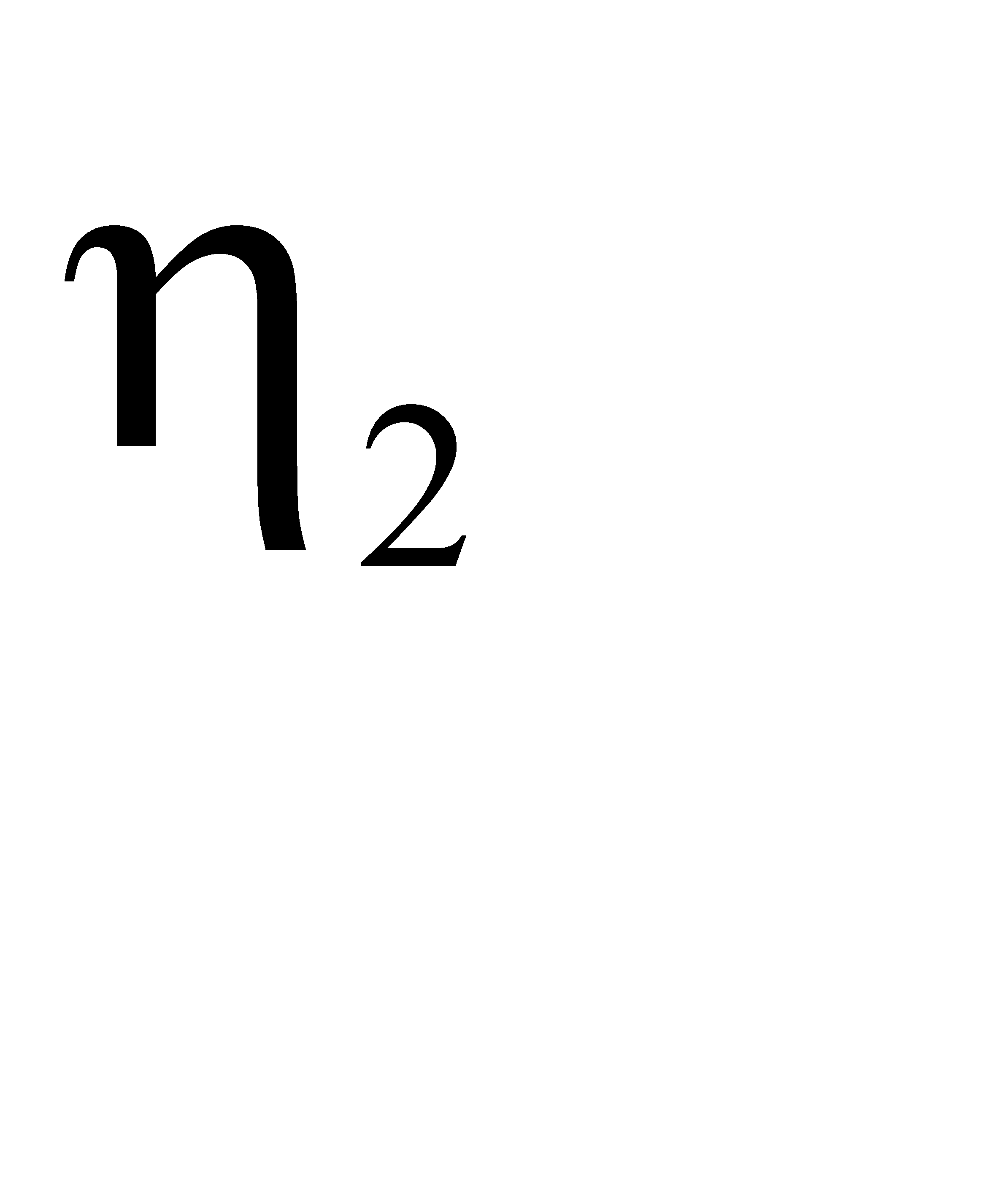
| G1, G2 |

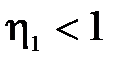
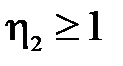

| 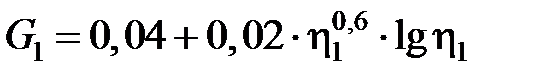
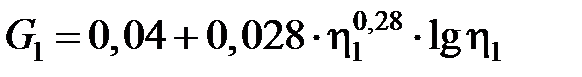
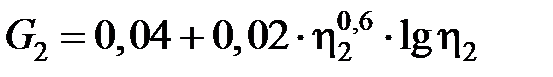

|
3.5. Значения функций 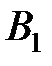 и
и 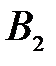 [3.1]
[3.1]
 , град. , град.
| 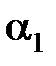 , , 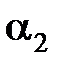
| |||||||
| 0,1 | 0,2 | 0,5 | ||||||
| 4,4 3,67 2,93 | 4,29 3,62 2,8 | 4,19 3,57 2,69 | 3,89 3,4 2,38 | 3,4 3,04 1,98 | 2,49 2,22 1,47 | 1,4 1,24 0,87 | 0,87 3,62 0,55 |
Средняя температура (температура резания)
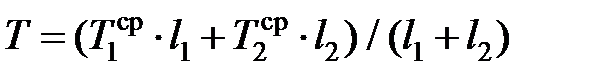 . (3.32)
. (3.32)
Температуру на контактных площадках при наличии смазочно-охлаждающей жидкости (СОЖ) определяют по зависимостям
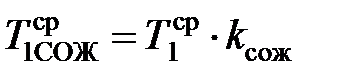 ;
; 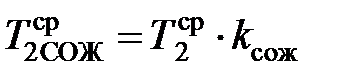 , (3.33)
, (3.33)
где kcож = 0,85 – поправочный коэффициент, учитывающий влияние охлаждающего действия СОЖ.
Приближенная зависимость для расчета температуры резания, не учитывающая влияние теплообмена на задней поверхности на температуру на передней поверхности [3.2]:
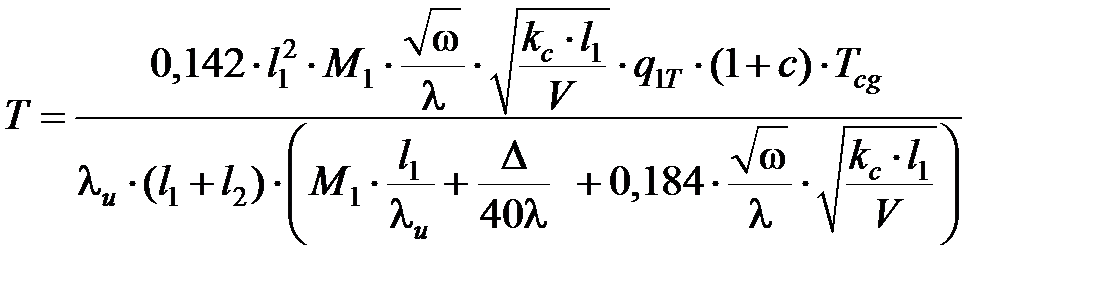 , (3.34)
, (3.34)
где 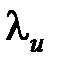 – коэффициент теплопроводности материала резца, кал/(с·см·°С);
– коэффициент теплопроводности материала резца, кал/(с·см·°С);  – высота нароста, мм (
– высота нароста, мм (  = 0, если нарост отсутствует);
= 0, если нарост отсутствует); 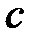 – коэффициент, зависящий от безразмерного критерия
– коэффициент, зависящий от безразмерного критерия 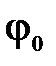 , определяемого по зависимости
, определяемого по зависимости
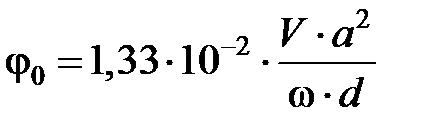 , (3.35)
, (3.35)
где 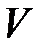 – скорость резания, м/мин;
– скорость резания, м/мин; 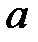 – толщина срезаемого слоя, мм;
– толщина срезаемого слоя, мм;  – коэффициент температуропроводности материала заготовки, см2/с;
– коэффициент температуропроводности материала заготовки, см2/с; 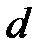 – диаметр обрабатываемой поверхности, мм.
– диаметр обрабатываемой поверхности, мм.
При 10-3 < 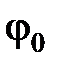 < 0,15
< 0,15  ;
;
при 0,15 < 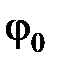 < 2
< 2 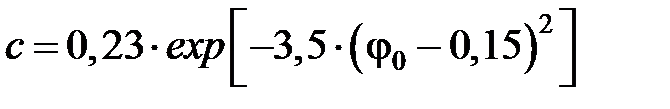 . (3.36)
. (3.36)
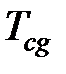 – температура в стружке от теплоты, выделяемой в зоне деформации:
– температура в стружке от теплоты, выделяемой в зоне деформации:
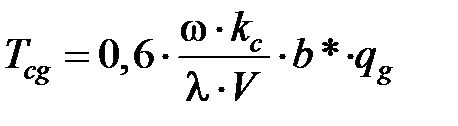 , (3.37)
, (3.37)
где 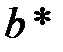 – доля теплоты, переходящей в стружку:
– доля теплоты, переходящей в стружку:
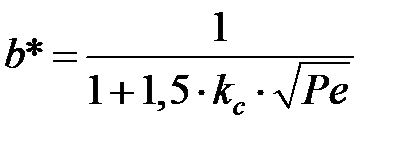 , (3.38)
, (3.38)
где Pe – критерий Пекле:
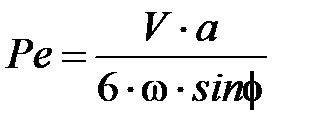 , (3.39)
, (3.39)
где 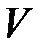 в м/мин;
в м/мин; 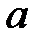 – мм;
– мм; 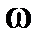 – см2/с.
– см2/с.
Значения функций М1 и М2 приведены в табл. 3.6.
Среднюю температуру передней поверхности резца можно определить по зависимости [3.4]
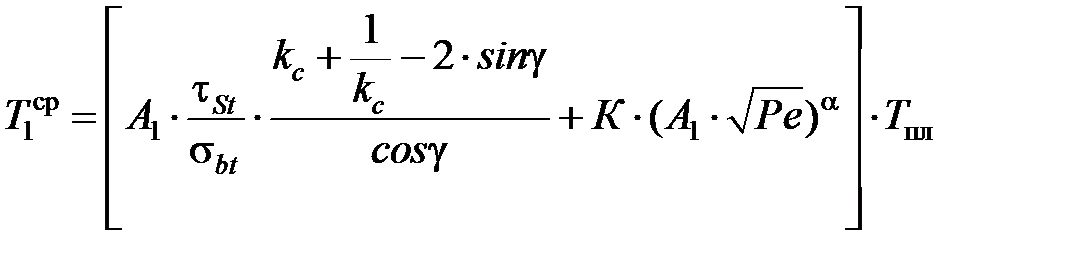 , (3.40)
, (3.40)
где α = 0,66 – коэффициент; 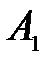 и
и  – безразмерные комплексы:
– безразмерные комплексы:
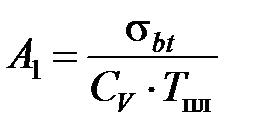 ;
; 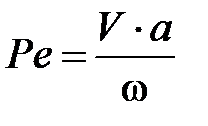 , (3.41)
, (3.41)
где 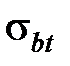 – предел прочности материала заготовки при растяжении, Па; К – коэффициент:
– предел прочности материала заготовки при растяжении, Па; К – коэффициент:
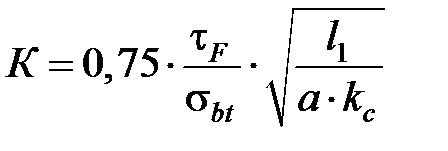 . (3.42)
. (3.42)
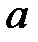 – толщина срезаемого слоя, м.
– толщина срезаемого слоя, м.
3.6. Значения функций М1 и М2 [3.2]
 , , 
| М1, М2 |
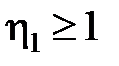
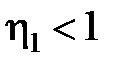
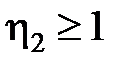

| 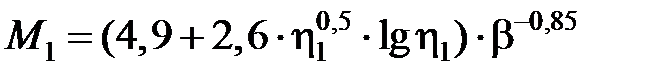
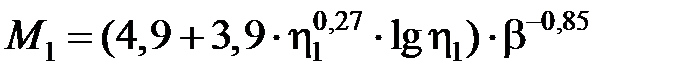

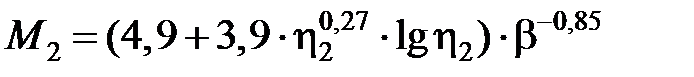
|
Зная среднюю температуру Т (температуру резания) и среднюю температуру передней поверхности резца 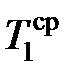 , можно определить среднюю температуру задней поверхности
, можно определить среднюю температуру задней поверхности 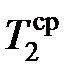 : из зависимости (3.32) для расчета
: из зависимости (3.32) для расчета 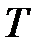 следует, что
следует, что
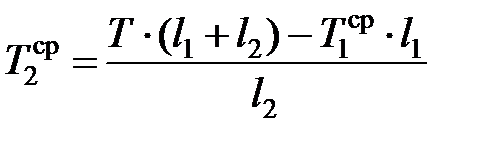 . (3.43)
. (3.43)
Дата добавления: 2021-01-26; просмотров: 475;











