Расчет изменения энтропии и энергии Гиббса в химических процессах
Поскольку энтропия является функцией состояния, то изменение энтропии в ходе химической реакции можно рассчитать как разность сумм энтропий продуктов реакции (конечных веществ) и реагентов (исходных веществ):
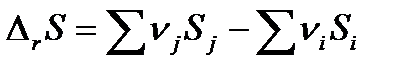
| (1.26) |
Пользуясь значениями стандартных энтропий веществ, изменение энтропии при протекании химической реакции в стандартных условиях можно рассчитать по формуле:
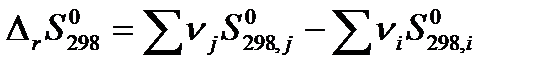
| (1.27) |
Изменение энтропии при химическом превращении при любой температуре T и стандартном давлении можно рассчитать исходя из зависимости энтропии каждого вещества, участвующего в реакции, от температуры. С использованием средних теплоемкостей изменение энтропии системы при протекании в ней химической реакции рассчитывается по уравнению:
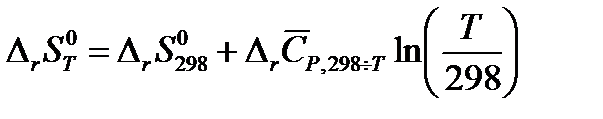
| (1.28) |
Пример: Рассчитаем изменение энтропии для реакции синтеза метанола при стандартных условиях.
Решение: Для расчетов воспользуемся справочными значениями стандартных энтропий, участвующих в реакции веществ (см. табл. 44 на стр.72 справочника [2]).
| Стандартная энтропия | СО(Г.) | + 2 Н2 (г.) | = СН3ОН(г.) |
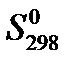 ,
Дж/(моль∙К) ,
Дж/(моль∙К)
| 197,55 | 130,52 | 239,76 |
Изменение энтропии при протекании химической реакции в стандартных условиях равно:
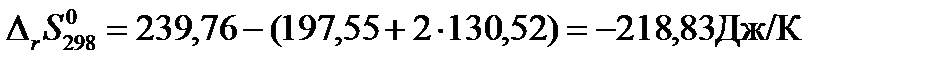
Пример: Рассчитаем изменение энтропии для реакции синтеза метанола при температуре 1000 К.
Решение: Для расчетов воспользуемся рассчитанным в примере 2 значением изменения средней теплоемкости системы за счет протекания в ней химической реакции в интервале температур от 298 до 1000К 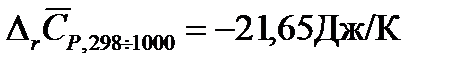 . Тогда Изменение энтропии для данной реакции при 1000К будет равно:
. Тогда Изменение энтропии для данной реакции при 1000К будет равно:
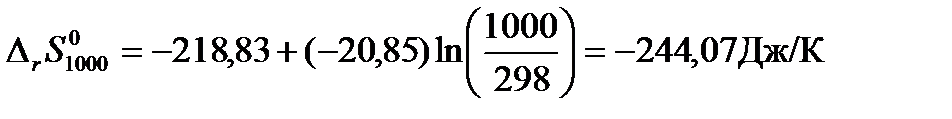
В соответствии с первым и вторым началами термодинамики для обратимого процесса можем записать
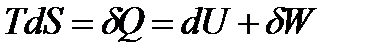
| (1.28) |
или
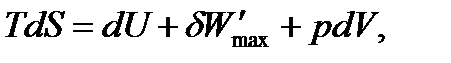
| (1.29) |
где 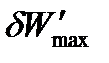 – максимальная полезная работа обратимого процесса, которая включает все виды работ, кроме работы расширения газа.
– максимальная полезная работа обратимого процесса, которая включает все виды работ, кроме работы расширения газа.
Это выражение называется объединённым уравнением первого и второго начал термодинамики, из него следует, что
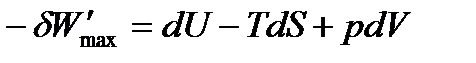
или по свойствам дифференциалов:
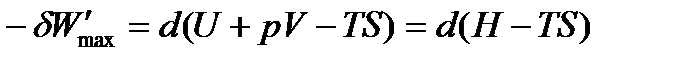
Обозначив разность (H – TS) как G и получим

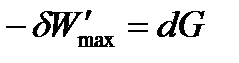
| (1.30) |
Таким образом, максимальная полезная работа в изобарно-изотермических условиях равна изменению термодинамической функции, которая получила название энергия Гиббса(изобарно-изотермический потенциал)и условно обозначается буквой G.
Для изохорно-изотермических условий (V = const, p = const) dV = 0, поэтому
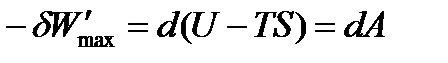
| (1.31) |
Таким образом, максимальная полезная работа в изохорно-изотермических условиях равна изменению термодинамической функции, которая получила название энергия Гельмгольца(изохорно-изотермический потенциал) и условно обозначается буквой A.
Большинство процессов в химико-технологических системах протекают в изобарно-изотермических условиях, для которых максимально полезная работа в ходе обратимого процесса равна убыли энергии Гиббса:
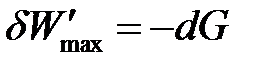
| (1.30а) |
Энергия Гиббса является функцией состояния. Изменение энергии Гиббса представляет собой ту часть полной энергии системы, которую в принципе можно превратить в максимальную полезную работу и является суммарной движущей силой процесса в изобарно-изотермических условиях.
В необратимых процессах работа всегда меньше, чем в обратимых. Тогда для необратимого и самопроизвольного процесса справедливо неравенство
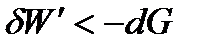 , ,
| (1.32) |
или для конечного процесса
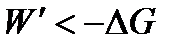
| (1.32а) |
Изменение энергии Гиббса в конечном процессе можно рассчитать как
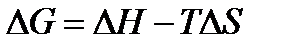 , ,
| (1.33) |
откуда
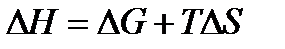
| (1.34) |
Это выражение также является математическим выражением второго начала термодинамики. Из него следует, что теплота процесса (ΔH) может быть лишь частично превращена в работу, которую характеризует свободная энергия Гиббса (ΔG). Функция TΔS – тепло, которое не может быть превращено в работу, TΔS называется связанной энергией.
Изменение стандартной энергии Гиббса при протекании реакции при любой температуре, в соответствии со вторым началом термодинамики, рассчитывается по уравнению:
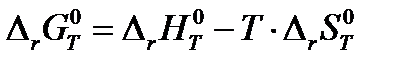 , ,
| (1.35) |
,
Пример: Рассчитаем изменение стандартной энергии Гиббса для реакции синтеза метанола при температуре 1000К.
Решение: Для расчетов воспользуемся рассчитанными в предыдущих примерах при температуре 1000К значениями теплового эффекта реакции синтеза метанола 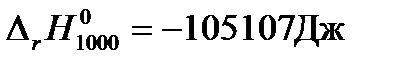 и изменения энтропии системы за счет протекания в ней химической реакции
и изменения энтропии системы за счет протекания в ней химической реакции 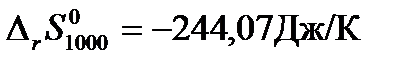 . Тогда изменение стандартной свободной энергии Гиббса для данной реакции при 1000К будет равно:
. Тогда изменение стандартной свободной энергии Гиббса для данной реакции при 1000К будет равно:
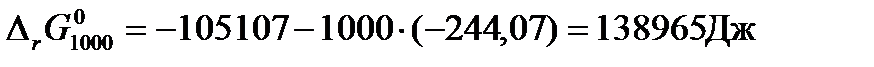
Дата добавления: 2021-01-26; просмотров: 643;











