ЖИДКОСТИ В КРУГЛЫХ ТРУБАХ

Ламинарное движение является упорядоченным слоистым течением без перемешивания частиц жидкости в потоке. При этом векторы скорости частиц будут параллельны оси потока, а поперечные скорости, перпендикулярные оси движения, отсутствуют. Так как движение имеет слоистый характер, то между слоями, которые движутся относительно друг друга, будут возникать силы внутреннего (вязкостного) трения и касательные напряжения. Движение жидкости подчиняется закону трения Ньютона.

Касательные напряжения при прямолинейном ламинарном движении согласно закону Ньютона

,

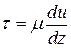где 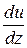- градиент скорости.

Рассмотрим установившееся ламинарное движение вязкой жидкости в круглой цилиндрической трубе радиусом 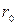(рис. 4.6). Так как 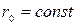, то движение является равномерным. Будем считать, что движущаяся жидкость в трубе разделяется на бесконечно большое количество бесконечно малых по толщине концентрически располагающихся цилиндрических слоев. Скорость в цилиндрическом слое, соприкасающемся со стенками трубы, в результате его прилипания равна нулю.

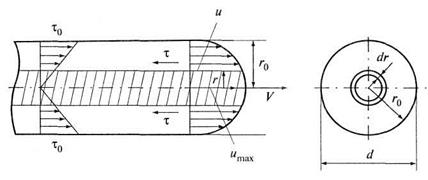
Рис. 4.6. К ламинарному движению жидкости в трубе

Касательные напряжения по поверхности рассматриваемого цилиндрического слоя толщиной dr

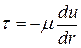. (4.48)

Знак минус в (4.48) обусловлен тем, что скорость 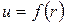при возрастании радиуса 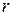убывает. Касательные напряжения согласно основному уравнению равномерного движения в слое жидкости

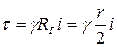, (4.49)

где 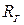- гидравлический радиус цилиндра жидкости радиусом , выделяемый в трубе:

.

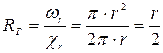Подставляя выражение (4.49) в формулу Ньютона, получаем

. (4.50)

Приращение скорости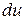

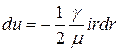. (4.51)

Интегрируя дифференциальное уравнение и считая , , найдем скорость

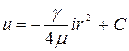_. (4.52)

Постоянную интегрирования С определим согласно условию, что у стенки трубы скорость 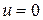при 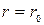, тогда

,

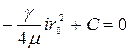откуда

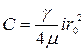. (4.53)

Подставляя С по формуле (4.53) в выражение (4.52), получаем следующее уравнение:

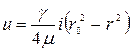. (4.54)

Уравнение (4.54) выражает распределение скорости в поперечном сечении трубы, которое представляет собой не что иное, как параболоид вращения относительно оси трубы. Задаваясь различными значениями, можно получить кривую распределения скоростей в сечении трубы. Кривая является параболой второй степени, ось которой - ось трубы (см. рис. 4.6).

Скорость по оси потока при 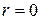- максимальная скорость определяемая как

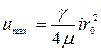. (4.55)

Согласно (4.49) значение касательных напряжений изменяется по сечению трубы линейно. На стенке трубы напряжения ( )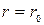

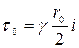. (4.56)

В центре трубы 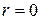и .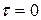

Эпюра распределения касательных напряжений по сечению трубы представлена на рис. 4.6.

Расход жидкости, проходящей по трубе, определяем, используя уравнение распределения скоростей при ламинарном течении (4.54).

Элементарный расход, проходящий через площадь цилиндрического слоя толщиной dr,

.

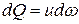Площадь цилиндрического слоя

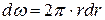. (4.57)

Тогда

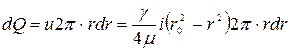. (4.58)

Интегрируем выражение (4.58) по всей поперечной площади живого сечения от 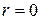до 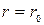, получаем

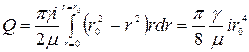. (4.59)

Средняя скорость ( 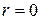) в поперечном сечении трубы

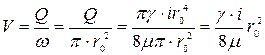. (4.60)

Среднюю скорость выразим через диаметр 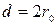и :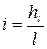

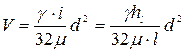. (4.61)

Сравниваем среднюю скорость 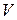с максимальной скоростью в трубе :

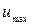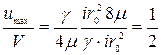. (462)

Средняя скорость в трубе при ламинарном движении в 2 раза меньше максимальной скорости, т.е.

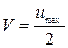. (4.63)

Потери напора по длине определим из формулы (4.61):

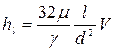_. (4.64)

Динамическая вязкость .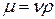

Формула представится после замены 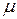, 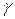в виде

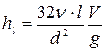. (4.65)

Данная зависимость (4.65) называется формулой Пуазеля-Гагена при определении потерь напора на трение по длине трубы для ламинарного режима.

Разделим и умножим формулу (4.65) на 2V, получим

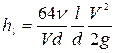, (4.66)

где 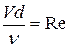(Re - число Рейнольдса),

тогда

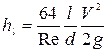. (4.67)

Приведем полученное выражение к виду формулы гидравлических потерь напора по длине (формула Вейсбаха-Дарси), обозначив

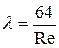, (4.68)

где 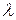- коэффициент гидравлического трения для ламинарного режима движения жидкости.

Таким образом, теоретически был определен коэффициент 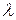при ламинарном движении (4.68).

Гидравлический уклон

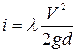(4.69)

♦ Пример 4.2

При движении жидкости в горизонтальном трубопроводе диаметром 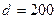мм расход Q=30 л/с. Разность пьезометрических высот на участке длиной 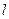=50 м составляет h=0,2 м. Определить кинематическую вязкость жидкости, полагая ламинарный режим движения.

Средняя скорость в трубопроводе

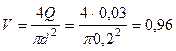м/c

Потери напора по длине участка трубопровода 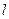=50 м согласно формуле Вейсбаха-Дарси

.

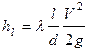Находим коэффициент гидравлического трения 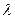, 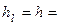0,2 м:

.

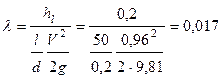При ламинарном режиме коэффициент гидравлического трения по формуле (4.68)

, .

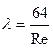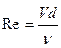Отсюда, зная 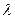, d, V, находим кинематическую вязкость жидкости:

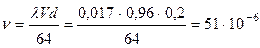м²/с.

Согласно табл. П1.3 такой вязкостью обладает одна из разновидностей минерального масла, например индустриальное.