Электромагнитные процессы в катушке с ферромагнитным сердечником

Будем считать катушку идеальной (рис.34), у которой активное сопротивление проводов равно нулю и отсутствуют потоки рассеяния. Напряжение 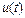уравновешивается ЭДС, наводимой в обмотке. На основании второго закона Кирхгофа имеем:

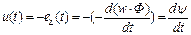, (45)

где 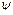− потокосцепление;

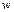– число витков обмотки;

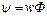- потокосцепление.

Рис.34. Катушка с сердечником

Решая последние два уравнения относительно 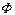, получим:

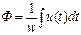. (46)

Если напряжение синусоидально, то магнитный поток также синусоидален и отстает от напряжения на 90^о.

Рис.35. Построение тока катушки с сердечником

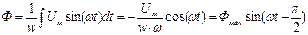, (47)

где 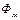− амплитудное значение магнитного тока:

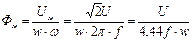. (48)

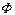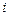Форма кривой тока катушки определяется кривой намагничивания (динамической петлей гистерезиса, построенной в координатах и ). Построение кривой тока 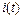проведено на рис.35. Из графика следует:

1. Кривая тока имеет явно несинусоидальную форму.

2. Чем больше напряжение ( 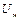), тем больше амплитуда магнитного потока, тем больше насыщение сердечника, что в свою очередь вызывает увеличение тока .

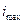3. Кривые тока и магнитного потока не совпадают по фазе. Ток опережает поток на угол магнитного запаздывания 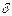, а это значит, что ток отстает от напряжения на угол 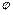< 90^о ( 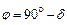). Из последнего следует, что активная мощность, потребляемая из сети ( хотя мы пренебрегли активным сопротивлением обмотки) больше нуля. Это объясняется потерями энергии, идущими на перемагничивание сердечника. Если пренебречь потерями, то кривая принимает вид, показанный на рис.36. В этом случае 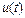и 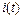совпадают по фазе.

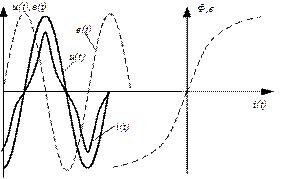
Рис.36. Форма тока без гистерезиса.

Если заменить несинусоидальную функцию тока некой эквивалентной синусоидой, можно построить на комплексной плоскости векторную диаграмму (рис.37.а). В соответствии с графиком на рис.35. токи и напряжения в комплексной форме можно записать так:

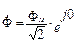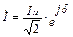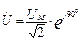, , , (49)

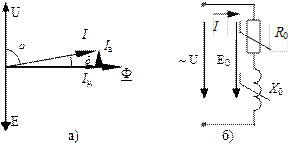
Рис.37. К расчету эквивалентного тока.

а) векторная диаграмма; б) эквивалентная схема замещения

где 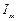-амплитуда эквивалентной синусоиды тока;

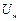- амплитуда входного напряжения;

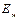- ЭДС, индуцируемая в катушке.

Вектор тока имеет две составляющие:

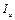- активная составляющая, совпадающая с напряжением по направлению, и определяющая активные потери на перемагничивание стали:

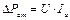, (50)

- реактивная составляющая, характеризующая реактивную мощность, потребляющую катушкой:

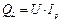. (51)

На рис.37.б. приведена схема замещения катушки со стальным сердечником, состоящая из активного сопротивления 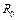и индуктивного - 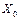. Следует отметить, что элементы 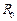и 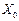– нелинейные.