Криптография с несколькими открытыми ключами

<119 120 121122123 124 125 >

Это обобщение RSA (см. раздел 19.3) [217, 212]. Модуль n является произведением двух простых чисел pи q. Однако вместо e и d, для которых edº1 mod ((p-1)(q-1)), выбирается tключей K_i, для которых выполняется

K₁* K₂*. . . *K_tº 1 mod ((p-1)(q-1))

Так как

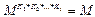
то эта схема оказывается схемой с несколькими ключами, описанная в разделе 3.5.

Если, например, используется пять ключей, то сообщение, зашифрованное ключами K₃ и K₅, может быть расшифровано с помощью K₁, K₂ и K₄.

C= modn

M= modn

Одним из применений этой схемы является подписание документа несколькими людьми. Представим ситуацию, когда для того, чтобы документ был действителен, он должен быть подписан и Алисой, и Бобом. Используются три ключа: K₁, K₂ и K₃.Алиса и Боб получают по одному ключу из первых двух, а третий опубликовывается.

(1) Сначала Алиса подписывает Mи посылает его Бобу.

M'= 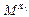mod n

(2) Боб может восстановить Mпо M'.

M = 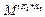modn

(3) Он может также добавить свою подпись.

M'' = modn

(4) Проверить подписи можно при помощи открытого ключа K₃.

M = modn

Обратите внимание, что для работоспособности этой системы нужна заслуживающая доверия сторона, которая установила бы систему и выдала ключи Алисе и Бобу. Та же проблема существует и в схеме [484]. Более тонкая схема описана в [695, 830, 700], Но усилия, предпринимаемые для проверки, пропорциональны количеству подписывающих. Новые схемы [220, 1200], основанные на схемах идентификации с нулевым знанием, преодолевают эти недостатки предшествующих систем.

<119 120 121122123 124 125 >

Дата добавления: 2021-01-26; просмотров: 284;

Поиск по сайту

Узнать еще