Отправитель и получатель. Сообщения и шифрование 9 глава

Вручение бита с помощью однонаправленных функций

Этот протокол использует однонаправленные функции:

(1) Алиса создает две случайных строки битов, R₁ и R₂.

R₁, R₂

(2) Алиса создает сообщение, состоящее из ее случайных строк и бита, который она хочет вручить (в действительности, это может быть и несколько битов).

(R₁, R₂, b)

(3) Алиса вычисляет однонаправленную функцию для сообщения и посылает результат вместе с одной из случайных строк Бобу.

H(R₁, R₂, b), R₁

Это сообщение Алисы является доказательством вручения. Использование однонаправленной функции на этапе (3) мешает Бобу, инвертируя функцию, определить бит.

Когда для Алисы придет время раскрыть свой бит, протокол продолжается:

(4) Алиса отправляет Бобу первоначальное сообщение.

(R₁, R₂, b)

(5) Боб вычисляет однонаправленную функцию для сообщения и сравнивает его и R₁ со значением однонаправленной функции и случайной строкой, полученными на этапе (3). Если они совпадают, то бит правилен.

Преимущество этого протокола перед предыдущим в том, что Бобу не нужно посылать никаких сообщений. Алиса посылает Бобу одно сообщение для вручения бита, а другое - для его раскрытия.

Не нужна и случайная строка Боба, так как результат Алисиного вручения - это сообщение, обработанное однонаправленной функцией. Алиса не может смошенничать и подобрать другое сообщение (R₁, R₂, b'), для которого H(R₁, R₂, b')= H(R₁, R₂, b). Посылая Бобу R₁, она вручает значение b. Если Алиса не сохранит в секрете R₂, то Боб получит возможность вычислить H(R₁, R₂, b') и H(R₁, R₂, b), получая возможность увидеть, что же он получил от Алисы.

Вручение бита с помощью генератора псевдослучайной последовательности

Этот протокол даже проще [1137]:

(1) Боб создает строку случайных битов и посылает ее Алисе.

R_В

(2) Алиса создает стартовую последовательность для генератора псевдослучайных битов. Затем для каждого бита в строке случайных битов Боба она посылает Бобу либо:

(a) выход генератора, если бит Боба равен 0, или

(b) XOR выхода генератора и бита Боба, если Бит Боба равен 1.

Когда для Алисы придет время раскрыть свой бит, протокол продолжается:

(3) Алиса посылает Бобу свою стартовую последовательность.

(4) Боб выполняет этап (2), убеждаясь, что Алиса действует честно.

Если строка случайных битов достаточно длинна, а генератор псевдослучайных битов непредсказуем, мошенничество Алисы практически невозможно.

Blob-объекты

Строки, которые Алиса посылает Бобу для вручения бита, иногда называют blob-объектами. Blob-объект - это последовательность битов, хотя протоколы этого и не требуют. Как сказал Жиль Брассар (Gilles Brassard), "Они могли бы быть сделаны и из волшебной пыли, если бы это было полезным" [236]. Blob-объекты обладают следующими четырьмя свойствами:

1. Алиса может вручить blob-объекты. Вручая blob-объект, она вручает бит.

2. Алиса может открыть любой blob-объект, который она вручила. Когда она открывает blob-объект, она может убедить Боба в значении бита, который был вручен вместе с blob-объектом. Следовательно, она не может открыть произвольный blob-объект, например, ноль или единицу.

3. Боб не может знать, каким образом Алиса может открыть blob-объект, который она вручила. Это остается справедливым, даже когда Алиса откроет другие blob-объекты.

4. Blob-объекты не несут никакой информации, кроме вручаемого Алисой бита. Сами по себе blob-объекты, также как и процесс, с помощью которого Алиса вручает и открывает их, не связаны не с чем другим, что Алиса хотела бы сохранить в секрете от Боба.

4.10 Подбрасывание "честной" монеты

Настало время процитировать Джо Килиана (Joe Kilian) [831]:

Алиса и Боб хотели сыграть в "орла и решку", но монеты у них не было. Алиса предложила простой способ подбрасывать монетку мысленно.

"Сначала вы задумываете случайный бит, затем я задумаю случайный бит. Затем мы выполняем над битами "исключающее или", - предложила она.

"Но если один из нас не будет задумывать биты случайным образом?", - спросил Боб.

"Это не важно. Если хотя бы один из битов действительно случаен, то и "исключающее или" битов должно быть действительно случайным", - ответила Алиса, и после минутного раздумья Боб согласился.

Немного спустя Алиса и Боб наткнулись на книгу по искусственному интеллекту, лежащую на обочине дороги. Алиса, добропорядочная гражданка, сказала: "Один из нас должен подобрать эту книгу и сдать ее в бюро находок". Боб согласился, и предложил использовать их протокол подбрасывания монетки, что бы определить, кто унесет книгу.

"Если полученный бит будет 0, то ты возьмешь книгу, а если 1 - то я", - сказала Алиса. " Какой у тебя бит?"

Боб ответил: "1".

"Ну вот, и у меня такой же", - лукаво заметила Алиса. - "Я думаю, у тебя сегодня неудачный день".

Очевидно, у протокола подбрасывания монетки есть серьезный дефект. Хотя это правда, что "исключающее или" действительно случайного бита, x, и любого независимо распределенного бита, y, дает в результате действительно случайный бит, протокол Алисы не гарантирует, что два бита будут распределены независимо. На самом деле нетрудно убедиться, что не существует мысленного протокола, который позволит двум независимым сторонам подбрасывать "честную" монетку. Алиса и Боб горевали, пока не получили письмо от неизвестного студента с дипломом по криптографии. Информация в письме была слишком теоретической, чтобы ее можно было применить для чего-то земного, но конверт, в котором пришло письмо, оказался чрезвычайно полезным.

Когда Алиса и Боб в следующий раз захотели подбросить монетку, они изменили первоначальный протокол. Сначала бит задумал Боб, но вместо того, чтобы открыть его немедленно, он записывает свой бит на листке бумаги и кладет листок в конверт. Затем Алиса объявляет свой бит. Наконец, Алиса и Боб достают бит Боба из конверта и вычисляют случайный бит. Этот бит уже действительно случаен, независимо от честности играющих. Алиса и Боб получили работающий протокол, социально значимая мечта криптографов осуществилась, и все они жили долго и счастливо.

Эти конверты выглядят весьма похожими на blob-объекты вручения бита. Когда Мануэль Блам (Manuel Blum) столкнулся с проблемой подбрасывания "честной" монеты по модему [194], он решил ее, используя протокол вручения бита:

(1) Алиса вручает случайный бит, используя любую из схем вручения бита, описанную в разделе 4.9.

(2) Боб загадывает свой бит.

(3) Алиса раскрывает бит Бобу. Боб выигрывает бросок, если он правильно загадал бит.

В общем случае, нам нужен протокол со следующими свойствами:

— Алиса должна "бросить монету" до того, как Боб загадает свой бит.

— Алиса не должна иметь возможности изменить результаты своего броска, узнав бит Боба.

— У Боба не должно быть возможности узнать результат броска перед тем, как он сделает свое предположение.

Существует несколько возможностей выполнить это.

Бросок монеты с помощью однонаправленных функций

Если Алиса и Боб договорятся об однонаправленной функции, протокол прост:

(1) Алиса выбирает случайное число, x. Она вычисляет y=f(x), где f(x) - однонаправленная функция.

(2) Алиса посылает y Бобу.

(3) Боб предполагает, что x четно или нечетно, и посылает свое предположение Алисе.

(4) Если предположение Боба правильно, результатом броска является "орел", если неправильно - то "решка". Алиса объявляет результат броска монеты и посылает x Бобу.

(5) Боб проверяет, что y=f(x).

Безопасность этого протокола обеспечивается однонаправленной функцией. Если Алиса сможет найти x и x', такие что x - четно, а x' - нечетно, и y=f(x)= f(x'),то она каждый раз сможет обманывать Боба. Кроме того, наименьший значащий бит f(x) должен быть некоррелирован с x. В противном случае Боб сможет обманывать Алису, по крайней мере иногда. Например, если f(x)в 75 процентах случаев четна, если x, у Боба будет преимущество. (Иногда наименьший значащий бит не является лучшим выбором для использования в приложении, потому что его вычисление может оказаться слишком простым.)

Бросок монеты с помощью криптографии с открытыми ключами

Этот протокол работает как с криптографией с открытыми ключами, так и с симметричной криптографией. Единственное условие - переключение алгоритма. То есть:

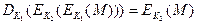
В общем случае это свойство не выполняется для симметричных алгоритмов, но справедливо для некоторых алгоритмов с открытыми ключами (например, RSA с идентичными модулями). Этот протокол:

(1) И Алиса, и Боб создают пары открытый ключ/закрытый ключ.

(2) Алиса создает два сообщения, одно для "орла", а второе - для "решки". Эти сообщения должны включать некоторую случайную строку, чтобы она могла подтвердить их подлинность на последующих этапах протокола. Алиса шифрует оба сообщения своим открытым ключом и посылает их Бобу в произвольном порядке.

E_A(M₁), E_A(M₂)

(1) Боб, которые не может прочитать не одно сообщение, случайным образом выбирает одно из них. (Он может посчитать их с помощью "Эники-беники ели вареники", воспользоваться компьютером для взлома протоколы или обратиться к цыганке.) Он шифрует выбранное сообщение своим открытым ключом и посылает его обратно Алисе.

E_В(E_A(M))

где M - M₁ или M₂.

(2) Алиса, которая не может прочитать полученное сообщение, расшифровывает его своим закрытым ключом и посылает обратно Бобу.

D_A(E_В(E_A(M)))= E_В(M₁), если M = M₁, или E_В(M₂), если M = M₂.

(3) Боб расшифровывает сообщение своим закрытым ключом, раскрывая результат броска монеты, и посылает расшифрованное сообщение Алисе.

D_В(E_В(M₁)) или D_В(E_В(M₂))

(4) Алиса читает результат броска монеты и проверяет, что случайная строка правильна.

(5) Алиса и Боб раскрывают пары своих ключей, чтобы каждый из сторон могла убедиться в отсутствии мошенничества.

Этот протокол самодостаточен. Любая сторона может немедленно обнаружить мошенничество другой, и не требуется третья сторона ни для участия в протоколе, ни в качестве арбитра после завершения протокола. Чтобы посмотреть, как это работает, давайте попытаемся смошенничать.

Если выиграть, смошенничав, хочет Алиса, у нее есть три возможных пути повлиять на результат. Во первых, она может зашифровать два сообщения для "орла" на этапе (2). Боб обнаружит это, когда Алиса раскроет свои ключи на этапе (7). Во вторых, она может использовать какой-то другой ключ для расшифровывания сообщения на этапе (4). Это приведет к бессмыслице, которую Боб и обнаружит на этапе (5). В третьих, она может объявить неправильным сообщение на этапе (6). Боб также обнаружит это на этапе (7), когда Алиса не сможет доказать, неправильность сообщения. Конечно, Алиса может отказаться от участия в протоколе на любом этапе, когда жульничество Алисы станет для Боба очевидным.

Если Боб захочет мошеннически выиграть, его положение ничуть не лучше. Он может неправильно зашифровать сообщение на этапе (3), но Алиса обнаружит обман, взглянув на заключительное сообщение на этапе (6). Он может заявить, что неправильно выполнил этап (5) из-за какого-то мошенничества со стороны Алисы, но эта форма жульничества вскроется на этапе (7). Наконец, он может послать Алиса сообщение о "решке" на этапе (5), независимо от расшифрованного сообщения, но Алиса сможет немедленно проверить достоверность сообщения на этапе (6).

Бросок монеты в колодец

Интересно отметить, что во всех этих протоколах Алиса и Боб узнают результат броска не одновременно. В каждом протоколе есть момент, когда одна из сторон (Алиса в первых двух протоколах и Боб в последнем) узнает результат броска, но не может изменить его. Эта сторона может, однако, задержать раскрытие результата для второй стороны. Это называется броском монет в колодец. Представьте себе высохший колодец. Алиса стоит рядом с колодцем, А Боб - немного подальше. Боб бросает монету, и она падает в колодец. Алиса может теперь заглянуть в колодец и увидеть результат, но она не может спуститься вниз и изменить его. Боб не сможет увидеть результат, пока Алиса не позволит ему подойти и заглянуть в колодец.

Генерация ключей с помощью броска монеты

Реальным применением этого протокола служит генерация сеансового ключа. Протоколы броска монеты позволяют Алисе и Бобу создать случайный сеансовый ключ так, что никто из них не сможет повлиять на то, каким будет этот ключ. Если Алиса и Боб зашифруют свои сообщения, процедура генерации ключа к тому же станет безопасной от злоумышленника.

4.11 Мысленный покер

Протокол, аналогичный протоколу броска монеты с помощью открытых ключей, позволяет Алисе и Бобу играть друг с другом в покер по электронной почте. Алиса вместо создания и шифрования двух сообщений, одного для "орла", а другого - для "решки", создает 52 сообщения М₁, М₂, ..., М₅₂, по числу карт в колоде. Боб случайным образом выбирает пять из них, шифрует своим открытым ключом и посылает обратно Алисе. Алиса расшифровывает сообщения и посылает их обратно Бобу, который расшифровывает их для определения своей "руки". Затем он случайным образом выбирает еще пять сообщений и, не изменяя их, посылает Алисе. Она расшифровывает их, и эти соответствующие карты становятся ее "рукой". В течение игры эта же процедура применяется для сдачи игрокам дополнительных карт. В конце игры Алиса и Боб раскрывают свои карты и пары ключей, чтобы каждый мог убедиться в отсутствии мошенничества.

Мысленный покер с тремя игроками

Покер интереснее, если в игре участвуют несколько человек. Базовый протокол мысленного покера легко может быть распространен на трех и более игроков. В этом случае криптографический алгоритм также должен быть коммутативным.

(1) Алиса, Боб и и Кэрол создают пары открытый ключ/закрытый ключ.

(2) Алиса создает 52 сообщения, по одному для каждой карты колоды. Эти сообщения должны включать некоторую уникальную случайную строку, чтобы Алиса могла проверить их подлинность на последующих этапах протокола. Алиса шифрует все сообщения своим открытым ключом и посылает их Бобу в произвольном порядке.

E_A(M_n)

(1) Боб, который не может прочитать не одно сообщение, случайным образом выбирает пять из них. Он шифрует их своим открытым ключом и посылает обратно Алисе.

E_В(E_A(M_n))

(2) Боб отправляет Кэрол оставшиеся 47 сообщений.

E_A(M_n)

(3) Кэрол, которая не может прочитать не одно сообщение, случайным образом выбирает пять из них. Она шифрует их своим открытым ключом и посылает Алисе.

E_С(E_A(M_n))

(4) Алиса, которая не может прочитать ни одно из полученных сообщений, расшифровывает их своим закрытым ключом и посылает обратно Бобу или Кэрол (в соответствии с тем, от кого она их получила).

D_A(E_В(E_A(M_n)))= E_В(M_n)

D_A(E_С(E_A(M_n)))= E_С(M_n)

(5) Боб и Кэрол расшифровывают сообщения своими ключами, чтобы узнать свои карты

D_В(E_В(M_n))

D_C(E_C(M_n))

(6) Кэрол случайным образом выбирает пять из оставшихся 42 сообщений и посылает Алисе.

E_A(M_n)

(7) Алиса расшифровывает сообщения, чтобы узнать свои карты.

D_A(E_A(M_n))

(8) В конце игры Алиса, Боб и Кэрол раскрывают свои карты и пары ключей, чтобы каждый мог убедиться в отсутствии мошенничества.

Дополнительные карты раздаются подобным же образом. Если карта нужна Бобу или Кэрол, любой из них берет зашифрованную колоду и повторяет протокол с Алисой, Если карта нужна Алисе, то тот, у кого сейчас находится зашифрованная колода, посылает ей случайную карту.

В идеале, этап (10) является обязательным. Свои "руки" в конце протокола должны открывать не все игроки, а только те, которые не спасовали. Так как этап (10) в протокол только для контроля мошенничества, возможны какие-нибудь улучшения.

В покере интересно только, не смошенничал ли победитель. Все остальные могут мошенничать сколько влезет, раз уж они все равно проигрывают. (В действительности это не совсем верно. Кто-то, проигрывая, может собирать данные о стиле игры в покер других игроков.) Итак, взглянем на случаи выигрыша различных игроков.

Если выигрывает Алиса, она раскрывает свою "руку" и свои ключи. Боб может использовать закрытый ключ Алисы для проверки правильности действий Алисы на этапе (2), то есть проверить, что каждое из 52 сообщений соответствует отдельной карте. Кэрол может проверить, что Алиса не лжет о своей "руке", шифруя карты открытым ключом Алисы и проверяя, что они соответствуют шифрованным сообщениям, которые она послала Алисе на этапе (8).

Если выигрывают Боб или Кэрол, победитель раскрывает свои карты и ключи. Алиса может убедиться в правильности карт, проверив свои случайные строки. Она может также убедиться, что сданы были именно эти карты, шифруя их открытым ключом победителя и проверяя, что они совпадают с зашифрованными сообщениями, полученными на этапах (3) или (5).

Этот протокол не защищен от сговора игроков-мошенников. Алиса и другой игрок могут объединиться и безнаказанно вместе надувать третьего игрока. Следовательно, важно проверять все ключи и случайные строки каждый раз, когда игроки раскрывают свои карты. И если вы сидите за виртуальным столом с двумя игроками, которые никогда одновременно не раскрывают свои карты, причем один из них сдает (в предыдущем протоколе это Алиса) кончайте игру.

Все это красиво в теории, но реализовать все это на компьютере весьма непросто. В реализации для трех игроков на трех различных Sparc-станциях восемь часов требуется только для тасования колоды, так что лучше поиграть в настоящий покер [513].

Вскрытия мысленного покера

Криптографы показали, что при использовании этими протоколами покера алгоритма с открытыми ключами RSA происходит небольшая утечка информации [453, 573]. Конкретно, если двоичное представление карт является квадратичным остатком (см раздел 11.3), то зашифрованные карты также являются квадратичным остатком. Это свойство может быть использовано для "крапления" некоторых карт - например, всех тузов. Это даст не много информации о сдачах, но в такой игре как покер даже чуть-чуть информации даст преимущество при длительной игре.

Шафи Голдвассер (Shafi Goldwasser) и Сильвия Микали (Silvia Micali) [624] разработали протокол умственного покера для двух игроков, который решает эту проблему, хотя из-за своей сложности он скорее имеет только теоретическое значение. Обобщенный протокол покера для n игроков, устраняющий проблему утечки информации, был разработан в [389].

Результаты других исследований протоколов игры в покер можно найти в [573, 1634, 389]. Усложненный протокол, позволяющий игрокам не раскрывать своих "рук", приведен в [390]. Дон Копперсмит (Don Coppersmith) рассматривает два способа мошенничества в умственном покере, использующем алгоритм RSA [370].

Анонимное распределение ключей

Хотя непохоже, чтобы кто-нибудь собирался использовать этот протокол для игры в покер по модему, Чарльз Пфлегер (Charles Pfleeger) рассматривает ситуацию, в которой этот тип протокола может оказаться полезным [1244].

Рассмотрим проблему распределения ключей. Если предположить, что люди не могут сами генерировать свои ключи(ключи должны иметь определенную форму, или должны быть подписаны некоторой организацией, или еще что-нибудь подобное), то для генерации и рассылки ключей придется создать Центр распределения ключей (Key Distribution Center, KDC). Проблема в том, что нужно найти такой способ распределения ключей, что никто, включая сервер, не сможет понять, кому какой ключ достался. Следующий протокол решает эту проблему:

(1) Алиса создает пару открытый ключ/закрытый ключ. В этом протоколе она сохраняет в секрете оба ключа.

(2) KDC генерирует непрерывный поток ключей.

(3) KDC шифрует ключи, один за другим, своим открытым ключом.

(4) KDC передает зашифрованные ключи, один за другим, по сети.

(5) Алиса случайным образом выбирает ключ.

(6) Алиса шифрует выбранный ключ своим открытым ключом.

(7) Алиса ждет какое-то время (достаточно большое, чтобы сервер не мог определить, какой ключ она выбрала) и посылает дважды зашифрованный ключ в KDC.

(8) KDC расшифровывает дважды зашифрованный ключ с помощью своего закрытого ключа, получая ключ, зашифрованный открытым ключом Алисы.

(9) Сервер посылает шифрованный ключ обратно Алисе.

(10) Алиса расшифровывает ключ с помощью своего закрытого ключа.

У находящейся где-то в середине протокола Евы нет ни малейшего представления о выбранном Алисой ключе. Она видит непрерывный поток ключей, создаваемых на этапе (4). Когда Алиса посылает ключ серверу на этапе (7), он шифруется ее открытым ключом, который также для этого протокола хранится в секрете. Способа связать это сообщение с потоком ключей у Евы нет. Когда ключ возвращается Алисе сервером на этапе (9), он также зашифрован открытым ключом Алисы. Ключ становится известным, только когда Алиса расшифровывает его на этапе (10).

Если вы используете RSA, в этом протоколе происходит утечка информации со скоростью, по меньшей мере, один бит на сообщение. Причиной этого снова являются квадратичные остатки. Если вы собираетесь использовать этот способ для распределения ключей, убедитесь, что эта утечка не приведет к каким-либо последствиям. Кроме того, поток ключей, создаваемый KDC должен быть достаточно большим, чтобы противостоять вскрытию грубым взломом. Конечно же, если Алиса не может верить KDC, то она не должна пользоваться его ключами. Мошенничающий KDC может предусмотрительно записывать все создаваемые им ключи. Тогда он сможет найти среди них ключ, выбранный Алисой.

Этот протокол также предполагает, что Алиса будет действовать честно. При использовании RSA существует ряд действий, которые может предпринять Алиса, чтобы получить больше информации, чем ей удалось бы при другом методе шифрования. В нашем сценарии эта проблема не существенна, но при других обстоятельствах она может стать важной.

4.12 Однонаправленные сумматоры

Алиса является членом организации "Заговорщики". Иногда ей приходится встречаться с другими членами в плохо освещенных ресторанах и шептать секреты налево и направо. Беда в том, что рестораны настолько плохо освещены, что она не может быть уверена, что человек, сидящий напротив нее за столом, тоже член организации.

"Заговорщики" могут выбирать из нескольких решений. Каждый может носить с собой список членов организации. Это влечет за собой две следующих проблемы. Во первых, теперь каждый должен носить с собой большую базу данных, и, во вторых, им придется как следует охранять этот список членов. Другим способом является использование идентификационных карт, выпущенных надежным секретарем. Дополнительным преимуществом этого способа является то, что и посторонние смогут проверять членов организации (всякие скидки в местной бакалейной лавке), до для этого нужен надежный секретарь. Никому из "заговорщиков" нельзя доверять до такой степени.

Новым решением является использование однонаправленного сумматора [116]. Это что-то похожее на однонаправленные хэш-функции, для которых выполняется требование коммутативности. То есть, можно хэшировать базы данных членов организации в произвольном порядке и получать одно и то же значение. Более того, можно добавлять новых членов в хэш-таблицу и получать новое хэш-значение, снова не зависящее от порядка.

Итак, вот что делает Алиса. Она выполняет расчет, используя множество всех имен членов организации, отличных от нее. Затем она сохраняет это полученное значение вместе со своим именем. Боб и другие члены делают то же самое. Теперь, когда Алиса и Боб встречаются в плохо освещенном ресторане, они просто обмениваются друг с другом вычисленными значениями и именами. Алиса убеждается, что результат, получаемый при добавлении имени Боба к значению Алисы, совпадает с результатом, получаемым при добавлении имени Алисы к значению равно значению Боба. Боб делает то же самое. Теперь они оба знают, что собеседник - также член организации. И в то же время никто не сможет определить личности других членов организации.

Более того, рассчитанные значения каждого члена могут быть выданы посторонним. Тогда Алиса сможет подтвердить свое членство постороннему (возможно, для членской скидки в буфете местной контрразведки), не показывая ему весь список членов.

Новых членов можно добавить просто послав по кругу новые имена. К несчастью, удалить члена можно только единственным путем: всем членам рассылается новый список и они пересчитывают свои значения. Но "заговорщикам" придется выполнять это действие только при отставке кого-то из членов, мертвые члены могут остаться в списке. (Странно, но это не создает проблемы.)

Это разумная идея применяется в ряде приложений, когда вы хотите достичь эффекта цифровой подписи без использования централизованной системы подписей.

4.13 Раскрытие секретов "все или ничего"

Представьте себе, что Алиса - бывший агент бывшего Советского Союза, а теперь безработная. Чтобы заработать, она продает секреты. Каждый, готовый заплатить названную цену, может купить секрет. У нее даже есть каталог. Все ее секреты с аппетитными названиями упорядочены по номерам: "Где Джимми Хоффа?", "Кто тайно контролирует Трехстороннюю комиссию?", "Почему Борис Ельцин всегда выглядит, как будто он проглотил живую лягушку?", и т.д.

Алиса не хочет отдавать два секрета по цене одного и не показывает даже части информации, касающейся любого из секретов. Боб, потенциальный покупатель, не хочет платить за кота в мешке. Он также не хочет сообщать Алисе, какие из секретов ему нужны. Это не ее дело, и, кроме того, тогда Алиса сможет добавить в свой каталог пункт "Секреты, которыми интересуется Боб".

Протокол покера не работает в этом случае, так как в конце этого протокола Алиса и Боб должны раскрыть свои карты друг другу. К тому же, существуют трюки, с помощью которых Боб может узнать сразу несколько секретов.

Решение называется раскрытием секретов "все или ничего" (all-or-nothing disclosure of secrets, ANDOS)[246], потому что если Боб получил любую информацию о любом из секретов Алисы, то он потерял возможность узнать что-либо еще о других ее секретах.

В криптографической литературе можно найти различные протоколы ANDOS. Некоторые из них обсуждаются в разделе 23.9.

4.14 Условное вручение ключей

Вот отрывок из введения в тему Сильвио Микали [1084]:

Сегодня подслушивание с разрешения суда является эффективным методом отдавать преступников в руки правосудия. По нашему мнению еще более важно, что это также предотвращает дальнейшее распространение преступления, удерживая от использования обычных сетей связи с незаконными целями. Следовательно, существует обоснованное беспокойство, что распространение криптографии с открытыми ключами может быть на руку преступным и террористическим организациям. Действительно, во многих законах предполагается, что соответствующие правительственные ведомства при определенных условиях, оговоренных законом, должны иметь возможность получить открытый текст любого обмена информацией по общедоступным сетям. В настоящее время many это может быть трактоваться, как требование к законопослушным гражданам либо (1) использовать слабые криптосистемы - т.е., криптосистемы, которые соответствующие власти (а также кто угодно!) смогут вскрыть с помощью умеренных усилий, или (2) заранее сообщать свои секреты властям. Не удивительно, что такая альтернатива законно встревожила многих заинтересованных граждан, создавая в результате мнение, что тайна личности должна стоять над национальной безопасностью и отправлением закона.

Условное вручение ключей является сутью продвигаемых правительством США программы Clipper и Стандарта условного шифрования (Escrowed Encryption Standard). Проблема в том, чтобы и обеспечить тайну личности, и в то же время позволить разрешенное судом подслушивание.

Escrowed Encryption Standard обеспечивает безопасность с помощью защищенного оборудования. У каждой микросхемы шифрования уникальный идентификационный номер (ID) и секретный ключ. Этот ключ делится на две части и хранится, вместе с ID, двумя различными организациями условного вручения. Всякий раз, когда микросхема шифрует файл данных, она сначала шифрует сеансовый ключ уникальным секретным ключом. Затем она передает зашифрованный сеансовый ключ и свой ID по каналу связи. Когда правоохранительные органы хотят расшифровать поток информации, зашифрованной одной из этих микросхем, они извлекают из потока ID, получают соответствующие ключи из организаций условного вручения, объединяют их с помощью операции XOR, расшифровывают сеансовый ключ и затем используют его для дешифрирования потока сообщений. Для защиты от мошенников в эту схему введены дополнительные усложнения, подробно описанные в разделе 24.16. Аналогичная схема может быть реализована и программно с использованием криптографии с открытыми ключами [77, 1579, 1580, 1581].