Отправитель и получатель. Сообщения и шифрование 6 глава
Удостоверение подлинности сообщений
Когда Боб получает сообщение от Алисы, как ему узнать, что это сообщение подлинно? Если Алиса подписала свое сообщение, то все просто. Цифровая подпись Алисы достаточна, чтобы подтвердить кому угодно подлинность ее сообщения.
Некоторую проверку подлинности предоставляют и симметричные алгоритмы. Когда Боб получает сообщение от Алисы, шифрованное их общим ключом, он знает, что это сообщение от Алисы. Никто больше не знает их ключа. Однако, у Боба нет возможности убедить в этом кого-то еще. Боб не может показать сообщение Тренту и убедить его, что оно отправлено Алисой. Трент может сделать вывод, что сообщение отправлено или Алисой, или Бобом (так как их секретный ключ никому больше не принадлежит), но у него нет способа определить, кто же конкретно автор сообщения.
Если сообщение не шифровано, Алиса может также использовать MAC. Это также убедит Боба в подлинности сообщения, но возникнут те же проблемы, что и для решений симметричной криптографии.
3.3 Удостоверение подлинности и обмен ключами
Эти протоколы объединяют удостоверение подлинности и обмен ключами для решения основной компьютерной проблемы: Алиса и Боб хотят безопасно обмениваться сообщениями, находясь на различных концах сети. Как могут Алиса и Боб обменяться секретным ключом, при этом сохраняя уверенность, что они обмениваются сообщениями друг с другом, а не с Мэллори? В большинстве протоколов предполагается, что каждому пользователю Трент выделяет отдельный секретный ключ, и перед началом работы протокола все ключи уже находятся у пользователей. Символы, используемые в этих протоколах, сведены в Табл. -1.
Табл. -1.
Символы, используемые в протоколах удостоверения подлинности и обмена ключами
| A | Имя Алисы |
| B | Имя Боба |
| EA | Шифрование ключом, выделенном Трентом Алисе |
| EB | Шифрование ключом, выделенном Трентом Бобу |
| I | Порядковый номер |
| K | Случайное сеансовое число |
| L | Время жизни |
| TA, TB | Метки времени |
| RA, RB | Случайные числа, выбранные Алисой и Бобом, соответственно |
Лягушка с широким ртом
Протокол "Лягушка с широким ртом" (Wide-Mouth Frog) [283, 284], возможно, является простейшим симметричным протоколом управления ключами, в котором используется заслуживающий доверия сервер. Алиса и Боб делят свой секретный ключ с Трентом. Эти ключи используются только для распределения ключей, а не для шифрования пользовательских сообщений. Вот как, используя два сообщения, Алиса передает Бобу сеансовый ключ:
(1) Алиса объединяет метку времени, имя Боба и случайный сеансовый ключ, затем шифрует созданное сообщение общим с Трентом ключом и посылает его Тренту вместе со своим именем.
A, EA(TA, B, K)
(2) Трент расшифровывает сообщение от Алисы. Затем он добавляет новую метку времени, имя Алисы и случайный сеансовый ключ, шифрует полученное сообщение общим с Бобом ключом. Трент посылает Бобу:
EB(TB, B, K)
Наибольшим допущением, сделанным в этом протоколе, является то, что Алиса обладает достаточной компетентностью для генерации хороших сеансовых ключей. Вспомните, что случайные числа генерировать совсем не просто, для этого может потребоваться кто-нибудь понадежнее Алисы.
Yahalom
В этом протоколе Алисы и Боб делят с Трентом секретный ключ [283, 284].
(1) Алиса объединяет свое имя и случайное число, и отправляет созданное сообщение Бобу.
A, RA
(2) Боб объединяет имя Алисы, ее случайное число, свое случайное число, шифрует созданное сообщение общим с Трентом ключом и посылает его Тренту, добавляя свое имя:
B, EB(A, RA, RB)
(3) Трент создает два сообщения. Первое включает имя Боба, случайный сеансовый ключ, случайные числа Боба и Алисы и шифруется ключом, общим для Трента и Алисы. Второе состоит из имени Алисы, случайного сеансового ключа и шифруется ключом, общим для Трента и Боба. Трент посылает оба сообщения Алисе:
EA(B, K, RA, RB), EB(A, K)
(4) Алиса расшифровывает первое сообщение, извлекает K и убеждается, что RA совпадает со значением, отправленным на этапе (1). Алиса посылает Бобу два сообщения. Одним является сообщение Трента, зашифрованное ключом Боба. Второе - это RB, зашифрованное сеансовым ключом.
EB(A, K), EK(RB),
(5) Боб расшифровывает первое сообщение, извлекает K и убеждается, что RB совпадает с отправленным на этапе (2).
В результате Алиса и Боб убеждены, что они общаются именно друг с другом, а не с третьей стороной. Нововведение состоит в том, что именно Боб первым обращается к Тренту, который только посылает одно сообщение Алисе.
Needham-Schroeder
В этом протоколе, изобретенном Роджером Неедхэмом (Roger Needham) и Майклом Шредером (Michael Schroeder) [1159], также используются симметричная криптография и Трент.
(1) Алиса посылает Тренту сообщение, содержащее ее имя, имя Боба и случайное число.
A, B, RA
(2) Трент генерирует случайный сеансовый ключ. Он шифрует сообщение, содержащее случайный сеансовый ключ и имя Алисы, секретным ключом, общим для него и Боба. Затем он шифрует случайное число Алисы, имя Боба, ключ, и шифрованное сообщение секретным ключом, общим для него и Алисы. Наконец, он отправляет шифрованное сообщение Алисе:
EA(RA, B, K, EB(K, A))
(3) Алиса расшифровывает сообщение и извлекает K. Она убеждается, что RA совпадает со значением, отправленным Тренту на этапе (1). Затем она посылает Бобу сообщение, зашифрованное Трентом ключом Боба.
EB(K, A)
(4) Боб расшифровывает сообщение и извлекает K. Затем он генерирует другое случайное число, RB. Он шифрует это число ключом K и отправляет его Алисе.
EK(RB)
(5) Алиса расшифровывает сообщение с помощью ключа K. Она создает число RB-1 и шифрует это число ключом K. Затем она посылает это сообщение обратно Бобу.
EK(RB-1)
(6) Боб расшифровывает сообщение с помощью ключа K и проверяет значение RB-1.
Вся эта возня с RA, RB, и RB-1 служит для предотвращения вскрытия с повторной передачей. При таком способе вскрытияМэллори может записать старые сообщения и впоследствии использовать их при попытке взломать протокол. Присутствие RA на этапе (2) убеждает Алису, что сообщение Трента достоверно и не является повторной передачей отклика, использованного при одном из предыдущих применений протокола. Когда Алиса успешно расшифрует RB и передает Бобу RB-1 на этапе (5), Боб убеждается, что сообщения Алисы не является повторной передачей сообщений, использованных при одном из предыдущих применений протокола.
Главной прорехой этого протокола является важность использованных сеансовых ключей. Если Мэллори получит доступ к старому K, он сможет предпринять успешное вскрытие [461]. Ему нужно только записать сообщения Алисы Бобу на этапе (3). Тогда, имея K, он может выдать себя за Алису:
(1) Мэллори посылает Бобу следующее сообщение:
EB(K, A)
(2) Боб извлекает K, генерирует RB и отправляет Алисе:
EK(RB)
(3) Мэллори перехватывает сообщение, расшифровывает его с помощью ключа K и посылает Бобу:
EK(RB-1)
(4) Боб убеждается, что сообщение "Алисы" состоит из RB-1.
Теперь Мэллори убедил Боба, что он и есть "Алиса". Более защищенный протокол, использующий метки времени, может противостоять этому вскрытию [461,456]. Метки времени добавляются к сообщению Трента на этапе (2) и шифруются ключом Боба: EB(K, A, T). Метки времени требуют надежной и точной системы единого времени, что само по себе нетривиальная проблема.
Компрометация ключа, общего для Трента и Алисы, будет иметь драматические последствия. Мэллори сможет использовать его с целью получения сеансовых ключей для обмена сообщениями с Бобом (или с кем-нибудь еще). Даже хуже, Мэллори продолжать подобные действия даже после замены ключа Алисы [90].
Неедхэм и Шредер пытались исправить эти проблемы в модифицированной версии своего протокола [1160]. Их новый протокол по существу совпадает с протоколом Otway-Rees, опубликованном в том же выпуске того же журнала.
Otway-Rees
Этот протокол также использует симметричную криптографию [1224].
(1) Алиса создает сообщение, состоящее из порядкового номера, ее имени, имени Боба и случайного числа. Сообщение шифруется ключом, общим для Алисы и Трента. Она посылает это сообщение Бобу вместе с порядковым номером, ее и его именами:
I, A, B, EA(RA, I, A, B)
(2) Боб создает сообщение, состоящее из нового случайного числа, порядкового номера, имени Алисы и имени Боба. Сообщение шифруется ключом, общим для Алисы и Боба. Он посылает это сообщение Тренту вместе с шифрованным сообщением Алисы, порядковым номером, ее и его именами:
I, A, B, EA(RA, I, A, B), EB(RB, I, A, B)
(3) Трент генерирует случайный сеансовый ключ. Затем он создает два сообщения. Одно, состоящее из случайного числа Алисы и сеансового ключа, шифруется ключом, общим для него и Алисы. Другое, состоящее из случайного числа Боба и сеансового ключа, шифруется ключом, общим для него и Боба. Он отправляет два этих сообщения вместе с порядковым номером Бобу:
I, EA(RA, K), EB(RB, K)
(4) Боб отправляет Алисе сообщение, шифрованное ее ключом, и порядковый номер:
I, EA(RA, K)
(5) Алиса расшифровывает сообщение, получая свои ключ и случайное число. Алиса убеждается, что при выполнении протокола они не изменились. Боб отправляет Алисе сообщение, шифрованное ее ключом, и порядковый номер.
Если все случайные числа правильны, а порядковый номер не изменился при выполнении протокола, Алиса и Боб убеждаются в подлинности друг друга и получают секретный ключ для обмена сообщениями.
Kerberos
Kerberos - вариант протокола Needham-Schroeder - подробно обсуждается в разделе 24.5. В базовом протоколе Kerberos Version 5 у Алисы и Боба общие ключи с Трентом. Алиса хочет генерировать сеансовый ключ для сеанса связи с Бобом.
(1) Алиса посылает Тренту сообщение со своим именем и именем Боба:
A, B
(2) Трент создает сообщение, состоящее из метки времени, времени жизни, L, случайного сеансового ключа и имени Алисы. Он шифрует сообщение ключом, общим для него и Боба. Затем он объединяет метку времени, время жизни, сеансовый ключ, имя Боба, и шифрует полученное сообщение ключом, общим для него и Алисы. Оба шифрованных сообщения он отправляет Алисе.
EA(T, L, K, B), EB(T, L, K, A)
(3) Алиса создает сообщение, состоящее из ее имени и метки времени, шифрует его ключом K и отправляет Бобу. Алиса также посылает Бобу сообщение от Трента, шифрованное ключом Боба:
EA(A, T), EB(T, L, K, A)
(4) Боб создает сообщение, состоящее из метки времени плюс единица, шифрует его ключом K и отправляет Алисе:
EK(T+1)
Этот протокол работает, но только если часы каждого пользователя синхронизированы с часами Трента. На практике эффект достигается синхронизацией с надежным сервером времени с точностью в несколько минут и обнаружением повторной передачи в течение определенного интервала времени.
Neuman-Stubblebine
Из-за недостатков системы или саботажа синхронизация часов может быть нарушена. Если часы сбиваются, против большинства протоколов может быть использован определенный способ вскрытия [644]. Если часы отправителя опережают часы получателя, Мэллори может перехватить сообщение отправителя и повторно использовать его позднее, когда метка времени станет текущей в месте нахождения получателя. Этот способ, называющийся вскрытием с подавлением повторной передачи, может привести к неприятным последствиям.
Этот протокол, впервые опубликованный в [820] и исправлен в [1162], пытается противостоять вскрытию с подавлением повторной передачи. Этот отличный протокол является улучшением Yahalom.
(1) Алиса объединяет свое имя и случайное число, и отправляет созданное сообщение Бобу.
A, RA
(2) Боб объединяет имя Алисы, ее случайное число и метку времени, шифрует созданное сообщение общим с Трентом ключом и посылает его Тренту, добавляя свое имя и новое случайное число:
B, RB, EB(A, RA, TB)
(3) Трент генерирует случайный сеансовый ключ. Затем он создает два сообщения. Первое включает имя Боба, случайное число Алисы, случайный сеансовый ключ, метку времени и шифруется ключом, общим для Трента и Алисы. Второе состоит из имени Алисы, сеансового ключа, метки времени и шифруется ключом, общим для Трента и Боба. Трент посылает оба сообщения Алисе вместе со случайным числом Боба:
EA(B, RA, K, TB), EB(A, K, TB), RB
(4) Алиса расшифровывает сообщение, зашифрованное ее ключом, извлекает K и убеждается, что RA совпадает со значением, отправленным на этапе (1). Алиса посылает Бобу два сообщения. Одним является сообщение Трента, зашифрованное ключом Боба. Второе - это RB, зашифрованное сеансовым ключом.
EB(A, K), EK(RB),
(5) Боб расшифровывает сообщение, зашифрованное его ключом, извлекает K и убеждается, что значения TB и RB те же, что и отправленные на этапе (2).
Если оба случайных числа и метка времени совпадают, Алиса и Боб убеждаются в подлинности дуг друга и получают секретный ключ. Синхронизация часов не требуется, так как метка времени определяется только по часам Боба, и только Боб проверяет созданную им метку времени.
У этого протокола есть еще одно полезное свойство - Алиса может использовать полученное от Трента сообщение для последующей проверки подлинности Боба в пределах некоторого времени. Предположим, что Алиса и Боб выполнили приведенный выше протокол, провели и завершили сеанс связи. Алиса и Боб могут повторно проверить подлинность друг друга, не обращаясь к Тренту.
(1) Алиса посылает Бобу сообщение, присланное ей Трентом на этапе (3) и новое случайное число.
EB(A, K, TB), R'A
(2) Боб посылает Алисе другое новое случайное число и случайное число, присланное Алисой, шифруя их сеансовым ключом связи.
R'B, EK(R'A)
(3) Алиса посылает Бобу его новое случайное число, шифруя его сеансовым ключом связи.
EK(R'B)
Новые случайные числа защищают от вскрытия с повторно передачей.
DASS
Протоколы Распределенной служба безопасности и проверки подлинности (Distributed Authentication Security Service, DASS), созданные в Digital Equipment Corporation, также обеспечивают обоюдную проверку подлинности и обмен ключами [604, 1519, 1518]. В отличие от предыдущего протокола DASS использует как криптографию с открытыми ключами, так и симметричную криптографию. И у Алисы, и у Боба есть свой закрытый ключ. Трент подписывает копии их открытых ключей.
(1) Алиса посылает Тренту сообщение, состоящее из имени Боба.
В
(2) Трент посылает Алисе открытый ключ Боба, KB, подписанный закрытым ключом Трента, T. Подписанное сообщение содержит имя Боба.
ST(B, KB)
(3) Алиса проверяет подпись Трента, убеждаясь, что она действительно получила открытый ключ Боба. Она генерирует случайный сеансовый ключ, K, и случайную пару ключей открытый/закрытый, Kp. Она шифрует метку времени ключом K, а затем подписывает время жизни, L, свое имя и своим закрытым ключом, KA. Наконец, она зашифровывает K открытым ключом Боба и подписывает его с помощью Kp. Все это она отправляет Бобу.
EK(TA),  (L, A, Kp),
(L, A, Kp),  (
(  (K))
(K))
(4) Боб посылает Тренту (это может быть другой Трент) сообщение, состоящее из имени Алисы.
А
(5) Трент посылает Бобу открытый ключ Алисы, KА, подписанный закрытым ключом Трента. Подписанное сообщение содержит имя Алисы.
ST(А, KА)
(6) Боб проверяет подпись Трента, убеждаясь, что он действительно получила открытый ключ Алисы. Затем он проверяет подпись Алисы и извлекает Kp. Боб использует свой закрытый ключ, извлекая K. Затем он расшифровывает TA, проверяя, что это сообщение - текущее.
(7) Если требуется обоюдная проверка подлинности, Боб шифрует новую метку времени ключом K и посылает ее Алисе.
EK(TВ)
(1) Алиса расшифровывает TВ ключом K, проверяя, что это сообщение - текущее.
SPX, продукт DEC, основан на DASS. Дополнительную информацию можно найти в [34].
Denning-Sacco
В этом протоколе также используется криптография с открытыми ключами [461]. Трент ведет базу данных, хранящую открытые ключи всех пользователей.
(1) Алиса посылает Тренту сообщение, состоящее из ее имени и имени Боба.
А, В
(2) Трент посылает Алисе открытый ключ Боба, KB, подписанный закрытым ключом Трента, T. Трент также посылает Алисе ее собственный открытый ключ, KА, подписанный закрытым ключом Трента.
ST(B, KB), ST(А, KА)
(3) Алиса посылает Бобу случайный сеансовый ключ и метку времени, подписав их своим закрытым ключом и зашифровав открытым ключом Боба, вместе с обоими подписанными ключами.
ЕВ(SА(K, ТА)), ST(А, KА), ST(В, KВ)
(4) Боб расшифровывает сообщение Алисы с помощью своего закрытого ключа и проверяет подпись Алисы с помощью ее открытого ключа. Он также убеждается, что метка времени правильна.
С этого момента Алиса и Боб получили K и могут провести безопасный сеанс связи. Это выгляди красиво, но есть одна тонкость - выполнив протокол с Алисой, Боб сможет выдать себя за Алису [5]. Смотрите:
(1) Боб посылает Тренту свое имя и имя Кэрол.
В, С
(2) Трент посылает Бобу подписанные открытые ключи Боба и Кэрол.
ST(B, KB), ST(С, KС)
(3) Боб посылает Кэрол подписанный случайный сеансовый ключ и метку времени, ранее полученные от Алисы, зашифровав их открытым ключом Кэрол, вместе с подтверждением Алисы и подтверждением Кэрол.
ЕС(SА(K, ТА)), ST(А, KА), ST(С, KС)
(4) Кэрол расшифровывает сообщение Алисы с помощью своего закрытого ключа и проверяет подпись Алисы с помощью ее открытого ключа. Она также убеждается, что метка времени правильна.
Теперь Кэрол считает, что она соединилась с Алисой, Боб успешно одурачил ее. Действительно, Боб сможет дурачить любого пользователя сети, пока не закончится срок действия метки времени. Но это легко можно исправить. Просто вставьте имена в шифрованное сообщение на этапе (3):
ЕВ(SА(А, В, K, ТА)), ST(А, KА), ST(В, KВ)
Теперь Боб не сможет повторно послать Кэрол старое сообщение, потому что оно явно предназначено для сеанса связи между Алисой и Бобом.
Woo-Lam
В этом протоколе также используется криптография с открытыми ключами [1610, 1611]:
(1) Алиса посылает Тренту сообщение, состоящее из ее имени и имени Боба.
А, В
(2) Трент посылает Алисе открытый ключ Боба, KB, подписанный закрытым ключом Трента, T.
ST(KB)
(3) Алиса проверяет подпись Трента. Затем она посылает Бобу свое имя и случайное число, шифрованное открытым ключом Боба.
А, ЕВ(RВ)
(4) Боб посылает Тренту свое имя, имя Алисы и случайное число Алисы, шифрованное открытым ключом Трента, KТ.
А, В,  (RA)
(RA)
(5) Трент посылает Бобу открытый ключ Алисы, KА, подписанный закрытым ключом Трента. Он также посылает Бобу случайное число Алисы, случайный сеансовый ключ, имена Алисы и Боба, подписав все это закрытым ключом Трента и зашифровав открытым ключом Боба.
SТ(KА),  (SТ (RA, К, А, В))
(SТ (RA, К, А, В))
(6) Боб проверяет подписи Трента. Затем он посылает Алисе вторую часть сообщения Трента, полученного на этапе (5), и новое случайное число, зашифровав все открытым ключом Алисы.
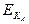 (SТ (RA, К, А, В), RВ)
(SТ (RA, К, А, В), RВ)
(7) Алиса проверяет подпись Трента и свое случайное число. Затем она посылает Бобу второе случайное число, шифрованное сеансовым ключом.
ЕК(RВ)
(8) Боб расшифровывает свое случайное число и проверяет, что оно не изменилось.
Другие протоколы
В литературе описано множество протоколов. Протоколы X.509 рассматриваются в разделе 24.9, KryptoKnight - в разделе 24.6, а Шифрованный обмен ключами (Encrypted Key Exchange) - в разделе 22.5.
Другим новым протоколом с открытыми ключами является Kuperee [694]. Ведется работа на протоколами, использующими маяки - заслуживающие доверия узлы сети, которые непрерывно и широковещательно передают достоверные метки времени [783].
Выводы
Из приведенных протоколов, как из тех, которые вскрываются, так и из надежных, можно извлечь ряд важных уроков:
— Многие протоколы терпят неудачу, так как их разработчики пытались быть слишком умными. Они оптимизировали протоколы, убирая важные элементы - имена, случайные числа и т.п. - и пытаясь сделать протоколы как можно более прозрачными [43, 44].
— Оптимизация - эта манящая ловушка - сильно зависит от сделанных предположений. Пример: наличие достоверного времени позволяет вам реализовать многие вещи, невозможные в противном случае.
— Выбираемый протокол зависит от архитектуры используемых средств связи. Хотите ли вы минимизировать размер сообщений или их количество? Могут ли сторона взаимодействовать каждый с каждым или круг их общения будет ограничен?
Именно подобные вопросы и привели к созданию формальных методов анализа протоколов.
3.4 Формальный анализ протоколов проверки подлинности и обмена ключами
Проблема выделения безопасного сеансового ключа для пары компьютеров (или людей) в сети настолько фундаментальна, что стала причиной многих исследований. Некоторые исследования заключались в разработке протоколов, подобных рассматриваемым в разделах 3.1, 3.2 и 3.3. Это, в свою очередь, привело к появлению более важной и интересной задачи: формальному анализу протоколов проверки подлинности и обмена ключами. Иногда прорехи в протоколах, кажущихся вполне надежными, обнаруживались спустя много лет после их разработки, и разработчикам потребовались средства, позволяющие сразу же проверять безопасность протокола. Хотя большая часть этого инструментария применима и к более общим криптографическим протоколам, особое внимание уделялось проверке подлинности и обмену ключами. Существует четыре основных подхода к анализу криптографических протоколов [1045]:
1. Моделирование и проверка работы протокола с использованием языков описания и средств проверки, не разработанных специально для анализа криптографических протоколов.
2. Создание экспертных систем, позволяющих конструктору протокола разрабатывать и исследовать различные сценарии.
3. Выработка требований к семейству протоколов, используя некую логику для анализа понятий "знание" и "доверие".
4. Разработка формальных методов, основанных на записи свойств криптографических систем в алгебраическом виде.
Полное описание этих четырех подходов и связанных с ними исследований выходит за рамки данной книги. Хорошее введение в эту тему дано в [1047, 1355], я же собираюсь коснуться только основных вопросов.
Первый из подходов пытается доказать правильность протокола, рассматривая его как обычную компьютерную программу. Ряд исследователей представляют протокол как конечный автомат [1449, 1565], другие используют расширения методов исчисления предиката первого порядка [822], а третьи для анализа протоколов используют языки описания [1566]. Однако, доказательство правильности отнюдь не является доказательством безопасности, и этот подход потерпел неудачу при анализе многих "дырявых" протоколов. И хотя его применение поначалу широко изучалось, с ростом популярности третьего из подходов работы в этой области были переориентированы.
Во втором подходе для определения того, может ли протокол перейти в нежелательное состояние (например, потеря ключа), используются экспертные системы. Хотя этот подход дает лучшие результаты при поиске "дыр", он не гарантирует безопасности и не предоставляет методик разработки вскрытий. Он хорош для проверки того, содержит ли протокол конкретную "дыру", но вряд ли способен обнаружить неизвестные "дыры" в протоколе. Примеры такого подхода можно найти в [987, 1521], а в [1092] обсуждается экспертная система, разработанная армией США и названная Следователем (Interrogator).
Третий подход гораздо популярнее. Он был впервые введен Майклом Бэрроузом (Michael Burrows), Мартином Абэди (Martin Abadi) и Роджером Неедхэмом. Они разработали формальную логическую модель для анализа знания и доверия, названную БАН-логикой[283, 284]. БАН-логика является наиболее широко распространена при анализе протоколов проверки подлинности. Она рассматривает подлинность как функцию от целостности и новизны, используя логические правила для отслеживания состояния этих атрибутов на протяжении всего протокола. Хотя были предложены различные варианты и расширения, большинство разработчиков протоколов до сих пор обращаются к оригинальной работе.
БАН-логика не предоставляет доказательство безопасности, она может только рассуждать о проверке подлинности. Она является простой, прямолинейной логикой, легкой в применении и полезной при поиске "дыр". Вот некоторые предложения БАН-логики:
Алиса считает X. (Алиса действует, как если бы X являлось истиной.)
Алиса видит X. (Кто-то послал сообщение, содержащее X, Алисе, которая может прочитать и снова передать X - возможно после дешифрирования.)
Алиса сказала X. (В некоторый момент времени Алиса послала сообщение, которое содержит предложение X. Не известно, как давно было послано сообщение, и было ли оно послано в течение текущего исполнения протокола. Известно, что Алиса считала X, когда говорила X.)
X ново. (X никогда не было послано в сообщении до текущего выполнения протокола.)
И так далее. БАН-логика также предоставляет правила для рассуждения о доверии протоколу. Для доказательства чего-либо в протоколе или для ответа на какие-то вопросы к логическим предложениям о протоколе можно применить эти правила. Например, одним из правил является правило о значении сообщения:
ЕСЛИ Алиса считает, что у Алисы и Боба общий секретный ключ, K, и Алиса видит Х, шифрованное K, и Алиса не шифровала X с помощью K,ТО Алиса считает, что Боб сказал X.
Другим является правило подтверждения метки времени:
ЕСЛИ Алиса считает, что X могло быть сказано только недавно, и, что Боб X когда-то сказал X, ТО Алиса считает, что Боб считает X.
БАН-анализ делится на четыре этапа:
(1) Преобразуйте протокол к идеальной форме, используя описанные выше предложения.
(2) Добавьте все предположения о начальном состоянии протокола.
(3) Присоедините логические формулы к предложениям, получая утверждения о состоянии системы после каждого предложения.
(4) Примените логические постулаты к утверждениям и предположениям, чтобы раскрыть состояние доверия участников протокола.
Авторы БАН-логики "рассматривают идеализированные протоколы как более ясные и полные описания, чем традиционные, найденные в литературе..." [283, 284]. Другие исследователи не так оптимистичны и подвергают это действие критике, так как при этом реальный протокол может быть искажен [1161, 1612]. Дальнейшие споры отражены в [221, 1557]. Ряд критиков пытается показать, что БАН-логика может и получить очевидно неправильные характеристики протоколов [1161] - см. контрдоводы в [285, 1509] - и что БАН-логика занимается только доверием, а не безопасностью [1509]. Подробное обсуждение приведено в [1488, 706, 1002].
Дата добавления: 2021-01-26; просмотров: 524;











