Отправитель и получатель. Сообщения и шифрование 10 глава
Микали называет свою идею честной криптосистемой [1084,10851. (Говорят, что правительство США заплатило Микали $1000000 за использование его патентов [1086, 1087] в своем стандарте Escrowed Encryption Standard, затем патент Микали купил Банковский трест.) В таких криптосистемах закрытый ключ делится на части и распределяется среди различных организаций. Как и схема с совместным использованием секрета, эти организации могут объединиться и восстановить закрытый ключ. Однако, части ключа обладают дополнительным свойством - их правильность может быть проверена независимо без восстановления закрытого ключа.
Алиса может создать свой собственный закрытый ключ и распределить его части среди n доверительных собственников. Ни один из них не может восстановить закрытый ключ Алисы. Однако каждый может проверить, что его часть - это правильная часть закрытого ключа. Алиса не может послать кому-то из доверительных собственников строку случайных битов и надеяться улизнуть. Если судебные власти разрешат подслушивание, соответствующие правоохранительные органы смогут воспользоваться постановлением суда для того, чтобы n доверительных собственников выдали свои части. Собрав все n частей, власти восстановят закрытый ключ и смогут подслушивать линии связи Алисы. С другой стороны, чтобы получить возможность восстановить ключ Алисы и нарушить ее тайну личности, Мэллори придется купить всех n доверительных собственников.
Вот как работает этот протокол:
(1) Алиса создает пару закрытый ключ/открытый ключ. Она разбивает закрытый ключ на несколько открытых и закрытых частей.
(2) Алиса посылает открытую часть и соответствующую закрытую часть каждому из доверительных собственников. Эти сообщения должны быть зашифрованы. Она также посылает открытый ключ в KDC.
(3) Каждый из доверительных собственников независимо выполняет вычисления над своими закрытой и открытой частями, чтобы убедиться в их правильности. Каждый доверительный собственник хранит закрытую часть в каком-нибудь надежном месте и отправляет открытую часть в KDC.
(4) KDC выполняет иное вычисление для открытых частей и открытого ключа. Убедившись, что все правильно, он подписывает публичный ключ и отправляет его обратно Алисе или помещает в какую-нибудь базу данных.
При наличии постановления суда о подслушивании каждый из доверительных собственников передает свою часть в KDC, и KDC получает возможность восстановить закрытый ключ. До этой передачи ни KDC, ни кто-либо из доверительных собственников не может самостоятельно восстановить закрытый ключ, для восстановления ключа нужны все доверительные собственники.
Любой алгоритм с открытыми ключами можно сделать "честным" подобным образом. Ряд конкретных алгоритмов рассматривается в разделе 23.10. В работах Микали [1084, 1085] обсуждаются пути объединения описанного с пороговой схемой, чтобы для восстановления закрытого ключа требовалось некоторое подмножество доверительных собственников (например, трое из пяти). Он также показывает, как объединить это с рассеянной передачей (см. раздел 5.5) так, чтобы доверительные собственники не знали, чей закрытый ключ восстанавливается.
"Честные" криптосистемы несовершенны. Преступник может использовать такую систему, применяя подсознательный канал (см. раздел 4.2.), чтобы вставить другой секретный ключ в свою информацию. Таким образом он может безопасно обмениваться информацией с кем-нибудь еще, используя подсознательный ключ и совершенно не волнуясь по поводу разрешенного судом подслушивания. Данная проблема решается другим протоколом, который называется отказоустойчивым условным вручением ключей [946, 833]. Этот алгоритм и протокол описывается в разделе 23.10.
Политика условного вручения ключей
Помимо правительственных планов относительно условного вручения ключей распространяются и коммерческие системы с условным вручением ключей. Возникает очевидный вопрос: какое преимущество от условного вручения ключей получает пользователь?
Ну, на самом деле никакого. Пользователь не получает от условного вручения ключей ничего такого, чего он и сам не смог бы обеспечить. Он и сам может создать резервную копию ключей, если захочет (см. раздел 8.8). Условное вручение ключей гарантирует, что полиция сможет подслушивать его разговоры или читать файлы данных, даже когда они шифрованы. Оно гарантирует, что NSA сможет подслушивать его международные звонки - без всякого ордера - хотя они и шифрованы. Может ему будет разрешено использовать такую криптографию с теми странами, для которых сейчас установлены запреты, но это сомнительное преимущество.
Недостатки условного вручения ключей весьма ощутимы. Пользователю приходится верить в безопасность действия организаций, занятых условным вручением ключей также, как и в честность занятых этим людей. Ему придется верить, что политика соответствующих организаций останется неизменной, правительство не поменяет законы, и те, кто имеет полномочия вскрыть его ключ, будут делать это по закону и с полной ответственностью. Вообразите нападение террористов на Нью-Йорк, какие бы ограничения не были бы сметены полицией, чтобы остановить последствия?
Трудно представить себе, что эти условные схемы шифрования, как говорят их защитники, будут использоваться без принуждения извне. Следующим очевидным шагом будет запрет на использование всех других способов шифрования. Это, вероятно, единственный способ добиться коммерческого успеха этой системы, и это, определенно, единственный способ заставить технически грамотных преступников и террористов использовать ее. Пока не ясно, насколько трудно будет объявить не-условную криптографию вне закона, или как это повлияет на криптографию как на академическую дисциплину. Как я могу исследовать программно ориентированные алгоритмы криптографии, не имея доступа к программному обеспечению устройств не-условного шифрования, нужна ли мне будет специальная лицензия?
И другие законные вопросы. Как условно врученные ключи повлияют на ответственность пользователей, должна ли становиться известной зашифрованная информация? Если правительство США пытается защитить органы условного вручения, не будет ли это косвенным свидетельством того, что если секрет скомпрометирован либо пользователем, либо органами условного вручения, то виновником будет признан пользователь?
Что если база данных главной службы условного вручения ключей, все равно государственной или коммерческой, будет украдена? Что, если правительство США попытается ненадолго скрыть этот факт? Ясно, что все эти вопросы повлияют на желание пользователей пользоваться условным вручением ключей. Если использование не будет добровольным, то пара скандалов вызовет рост политического давления с целью либо сделать использование подобных систем добровольным, либо ввести новые сложные правила в этой отрасли.
Еще более опасным будет скандал, когда выяснится, что годами под наблюдением находился политический оппонент текущей администрации или некий громкоголосый критик спецслужб и полицейских ведомств. Это сильно настроит общественное мнение против условного шифрования.
Если ключи подписей будут шифроваться тем же способом, что и ключи шифрования, возникнут дополнительные моменты. Допустимо ли для властей использовать ключи подписей для проведения операции против подозреваемого преступника? Будет ли признана судом подлинность подписей, основанных на ключах с условным вручением? Чем в действительности будут владеть пользователи, если власти действительно используют их ключи пользователей для подписи какого-то невыгодного контракта, для поддержки определенных отраслей промышленности, или просто, чтобы украсть деньги?
Глобальное распространение криптографии рождает дополнительные вопросы. Будут ли схемы условного вручения ключей совместимы в различных странах? Захотят ли транснациональные корпорации смириться с существованием в каждой стране своих условно врученных ключей, совместимых с различным местным законодательством? Без обеспечения совместимости исчезает одно из пропагандируемых преимуществ схемы с условным вручением ключей (международное использование мощных средств криптографии).
Что если ряд стран не примет на веру надежность организаций, связанных с условным вручением ключей? Как будут пользователи вести свои дела в этих странах? Будут ли признаны судами их электронные контракты, или тот факт, что ключи их подписей условно хранятся в США, позволит им утверждать где-нибудь в Швейцарии, что этот электронный контракт мог подписать кто-то другой? Или для людей, которые ведут дела в подобных странах, будут специальные исключения?
А что делать с промышленным шпионажем? Где гарантии, что страны, занимающиеся сейчас промышленным шпионажем для своих важнейших или государственных предприятия, не воспользуются для этого системами с условным вручением ключей? В самом деле, так как ни одна страна не собирается позволять другим странам следить за своими разведывательными операциями, распространение условного шифрования возможно приведет к увеличению подслушивания.
Даже если страны, в которых соблюдаются гражданские права, будут использовать условность такого шифрования только для законного преследования преступников и террористов, где-нибудь этим обязательно воспользуются для выслеживания диссидентов, шантажа политических оппонентов, и т.п. Цифровые линии связи предоставляют возможность гораздо более тщательно, чем это было возможно в аналоговом мире, контролировать действия граждан, их мнения, Digital communications offer the opportunity to do a much more thorough lob of monitoring citizens' actions, opinions, доходы и объединения.
Не ясно, не будет ли через 20 лет продажа системы с условным вручением ключей Турции или Китаю походить на продажу электрических дубинок Южной Африке в 1970 году или на строительство химического завода в Ираке в 1980 году. Даже хуже, легкое и незаметное подслушивание линий связи может искусить многие правительства, которые раньше, возможно, этим и не занимались, следить за корреспонденцией своих граждан. И нет гарантии, что либеральные демократии устоят перед подобным искушением.
5 Развитые протоколы
5.1 Доказательства с нулевым знанием
А вот другая история:
| Алиса: | "Я знаю пароль компьютера Федеральной Резервной Системы, компоненты секретного соуса МакДональдс и одержание 4-го тома Дональда Кнута". |
| Боб: | "Нет, ты не знаешь". |
| Алиса: | "Нет, я знаю". |
| Боб: | "Не знаешь". |
| Алиса: | "Нет, знаю". |
| Боб: | "Докажи". |
| Алиса: | "Хорошо, я скажу тебе". Она шепчет Бобу на ухо. |
| Боб: | "Это интересно. Теперь я тоже это знаю и собираюсь рассказать это все Вашингтон Пост". |
| Алиса: | "Оооой". |
К несчастью, обычно Алиса может доказать что-нибудь Бобу, только рассказав ему все. Но тогда он тоже получит все сведения. Затем Боб может выложить полученные сведения кому угодно, и Алиса ничего не сможет с этим поделать. (В литературе для описания этих протоколов часто используются различные персонажи. Пегги обычно доказывает, а Виктор проверяет. Именно эти имена появляются в используемых примерах вместо Алисы и Боба.)
Используя однонаправленные функции, Пегги сможет провести доказательство с нулевым знанием [626]. Этот протокол доказывает Виктору, что у Пегги действительно есть информация, но не дает Виктору не малейшей возможности узнать, что это за информация.
Эти доказательства принимают форму интерактивного протокола. Виктор задает Пегги ряд вопросов. Если Пегги знает секрет, то она ответит на все вопросы правильно. Если секрет ей неизвестен, у нее есть некоторая вероятность - 50 процентов в следующих примерах - ответить правильно. После примерно 10 вопросов Виктор убедится, что Пегги знает секрет. Но ни один из вопросов или ответов не даст Виктору ни малейших сведений об информации Пегги, но докажет знание Пегги этой информации.
Базовый протокол с нулевым знанием
Жан-Жак Кискатер (Jean-Jacques Quisquater) и Луи Гилу (Louis Guillou) поясняют нулевое знание историей о пещере [1281]. У пещеры, показанной на Рис.-1, есть секрет. Тот, кто знает волшебные слова может открыть потайную дверь между C и D. Для всех остальных оба прохода ведут в тупик.
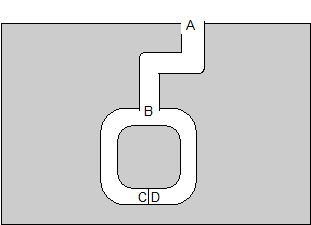
Рис. -1. Пещера нулевого знания
Пегги знает секрет пещеры. Она хочет доказать свое знание Виктору, но не хочет раскрывать волшебных слов. Вот как она убеждает его:
(1) Виктор находится в точке А.
(2) Пегги проходит весь путь по пещере, либо до точки C, либо до точки D.
(3) После того, как Пегги исчезнет в пещере, Виктор переходит в точку В.
(4) Виктор кричит Пегги, спрашивая ее либо о:
(a) или выйти из левого прохода
(b) выйти из правого прохода.
(5) Пегги исполняет его просьбу, при необходимости используя волшебные слова, чтобы отпереть дверь.
(6) Пегги и Виктор повторяют этапы (1) - (5) n раз.
Предположим, что у Виктора есть видеокамера, и он записывает все, что видит. Он записывает, как Пегги исчезает в пещере, записывает, как он сам кричит, указывая, где Пегги должна появиться, записывает как Пегги появляется. Он записывает все nтестов. Если он покажет эту видеозапись Кэрол, поверит ли она, что Пегги знает волшебные слова, отпирающие дверь? Нет. А что если Пегги и Виктор заранее договорились, что Виктор будет кричать, а Пегги будет делать вид, что она прошла весь путь. Тогда она будет каждый раз выходить из указанного Виктором места, не зная волшебных слов. Или они могли сделать по другому. Пегги входит в один из проходов и Виктор случайным образом выкрикивает свои просьбы. Если Виктор угадывает правильно, хорошо, если нет - они вырежут эту попытку из видеозаписи. В любом случае Виктор может получить видеозапись, показывающую в точности ту последовательность, которая получилась бы, если бы Пегги знала волшебные слова.
Этот опыт показывает две вещи. Во первых, Виктор не может убедить третью сторону в правильности доказательства. И во вторых, данный протокол является протоколом с нулевым знанием. Если Пегги не знает волшебных слов, то очевидно, что Виктор не узнает ничего из просмотра видеозаписи. Но так как нет способа отличить реальную видеозапись от подделанной, то Виктор не может ничего узнать из реального доказательства - это и есть нулевое знание.
Методика, используемая в этом протоколе, называется разрезать и выбрать из-за того, что она похож на классический протокол честного деления чего-либо:
(1) Алиса делит некую вещь пополам.
(2) Боб выбирает одну из половин себе.
(3) Алиса забирает оставшуюся половину.
В интересах Алисы честно разделить на этапе (1), потому что Боб выберет на этапе (2) ту половину, которая ему больше нравится. Майкл Рабин (Michael Rabin) первым использовал в криптографии технику "разрезать и выбрать" [1282]. Понятия интерактивного протокола и нулевого знания были формализованы позже [626, 627].
Протокол "разрезать и выбрать" работает, потому что Пегги не может несколько раз подряд угадывать, откуда Виктор попросит ее выйти. Если Пегги не знает секрета, он может выйти только из того прохода, в который она зашла. В каждом раундепротокола ее вероятность (иногда называемая аккредитацией) угадать, с какой стороны Виктор попросит ее выйти, составляет 50 процентов, поэтому ее вероятность обмануть Виктора также равна 50 процентам. Вероятность обмануть его в двух раундах составит 25 процентов, а во всех n раундах - один шанс из 2n. После 16 раундов у Пегги 1 шанс из 65536 обмануть Виктора. Виктор может уверенно предположить, что если все 16 доказательств Пегги правильны, то она действительно знает тайные слова, открывающие дверь между точками C и D. (Аналогия с пещерой несовершенна. Пегги может просто входить с одной стороны и выходить с другой, протокол "разрезать и выбрать" не нужен. Однако, он необходим с для нулевого знания с математической точки зрения.)
Предположим, что Пегги известна некоторая информация, которая является решением трудной проблемы. Базовый протокол нулевого знания состоит из нескольких раундов.
(1) Пегги использует свою информацию и случайное число для преобразования одной трудной проблемы в другую, изоморфную оригинальной проблеме. Затем она использует свою информацию и случайное число для решения новой трудной проблемы.
(2) Пегги вручает решение новой проблемы, используя схему вручения бита.
(3) Пегги раскрывает Виктору новый экземпляр проблемы. Виктор не может использовать эту новую проблему для получения информации о первоначальной проблеме или ее решении.
(4) Виктор просит Пегги либо
(a) доказать ему, что новая и старая проблема изоморфны (т.е., два различных решения для двух связанных проблем), либо
(b) открыть решение, полученное на этапе (2) и доказать, что это решение новой проблемы.
(5) Пегги исполняет его просьбу.
(6) Пегги и Виктор повторяют этапы (1) - (5) n раз.
Помните видеокамеру в протоколе для пещеры? Здесь вы можете сделать то же самое. Виктор может записать обмен между ним и Пегги. Он не сможет использовать эту запись для убеждения Кэрол, но он всегда может сговориться с Пегги с целью создать имитатор, который подделывает информацию Пегги. Этот аргумент может быть использован, чтобы доказать, что используется доказательство с нулевым знанием.
Математическая основа доказательства этого типа сложна. Проблемы и случайное преобразование должны выбираться осторожно, чтобы Виктор не получил никакой информации о решении оригинальной проблемы, даже после многих повторений протокола. Не все трудные проблемы можно использовать для доказательств с нулевым знанием, но большинство из них.
Изоморфизм графа
Объяснение этого понятия, пришедшего из теории графов [619, 622], может занять некоторое время. Граф представляет собой сеть линий ,соединяющих различные точки. Если два графа идентичны во всем, кроме имен точек, они называются изоморфными. Для очень больших графов доказательство их изоморфности может потребовать веков компьютерного времени, это одна из так называемых NP-полныхпроблем, рассматриваемых в разделе 11.1.
Предположим, что Пегги знает об изоморфности двух графов, G1 и G2. Следующий протокол докажет Виктору знание Пегги:
(1) Пегги случайным образом тасует G1, получая другой граф, Н, который изоморфен G1. Так как Пегги знает об изоморфизме Н и G1, то ей также известен изоморфизм между Н и G2. Для любого другого поиск изоморфизма между Н и G1 или Н и G2 является такой же трудной задачей, как и поиск изоморфизма между G1 и G2.
(2) Пегги посылает Н Виктору.
(3) Виктор просит Пегги либо
(a) доказать, что Н и G1 изоморфны, либо
(b) доказать, что Н и G2 изоморфны.
(4) Пегги исполняет его просьбу. Она либо:
(a) доказывает, что Н и G1 изоморфны, не доказывая, что Н и G2 изоморфны, либо
(b) доказывает, что Н и G2 изоморфны, не доказывая, что Н и G1 изоморфны.
(5) Пегги и Виктор повторяют этапы (1) - (4) n раз.
Если Пегги не знает об изоморфизме между G1 и G2, она не сможет создать граф Н, изоморфный обоим графам. Она может создать либо граф, который изоморфен G1, либо граф, который изоморфен G2. Как и в предыдущем примере у нее только 50 шансов из 100 угадать, какое доказательство потребует от нее Виктор на этапе (3).
Этот протокол не дает Виктору никакой полезной информации, помогающей ему из ответов Пегги установить изоморфизм между G1 и G2. Так как Пегги для каждого нового раунда протокола генерирует новый граф Н, Виктор не сможет получить информацию независимо от того, из скольких раундов будет состоять их протокол. Он не сможет из ответов Пегги установить изоморфизм между G1 и G2.
В каждом раунде Виктор получает новое случайное преобразование Н, вместе с изоморфизмом между Н и G1 или G2. Виктор может также создать что-то подобное самостоятельно. Так как Виктор может создать имитацию протокола, это действительно доказательство с нулевым знанием.
Гамильтоновы циклы
Вариант этого примера был впервые представлен Мануэлем Блюмом (Manuel Blum) [196]. Пегги знает кружной, продолжительный путь вдоль линий графа, который проходит через каждую точку только один раз. Этот путь называется гамильтоновым циклом. Поиск гамильтонова цикла является другой тяжелой задачей. У Пегги есть эта информация - она, возможно, получила ее создав граф с конкретным гамильтоновым циклом - и она хочет доказать Виктору, что эта информация ей известна.
Пегги знает гамильтонов цикл графа, G. Виктору известен G, но не его гамильтонов цикл. Пегги хочет доказать Виктору, что она знает гамильтонов цикл, не раскрывая самого цикла. Вот как она должна действовать:
(1) Пегги случайным образом преобразовывает G. Она передвигает точки и изменяет их метки, создавая новый граф, H. Поскольку G и Hтопологически изоморфны (т.е., это один и тот же граф), если ей известен гамильтонов цикл G, то она легко может найти гамильтонов цикл H. Если она не сама создает H, определение изоморфизма между двумя графами будет являться другой сложной проблемой, решение которой также потребует веков компьютерного времени. Затем она шифрует H, получая H'. (Должно использоваться вероятностное шифрование каждой строчки H, то есть, шифрованный 0 или шифрованная 1 для каждой линии H.)
(2) Пегги передает Виктору копию H.
(3) Виктор просит Пегги либо:
(a) доказать ему, что Н' - это зашифрованная изоморфная копия G, либо
(b) показать ему гамильтонов цикл для Н.
(4) Пегги исполняет его просьбу. Она либо:
(a) доказывает, что Н' - это зашифрованная изоморфная копия G, раскрывая преобразования и расшифровывая все, не показывая гамильтонов цикл для G или Н, либо
(b) показывает гамильтонов цикл для Н, расшифровывая только те строки, которые образуют гамильтонов цикл, не доказывая, что Н и G топологически изоморфны.
(5) Пегги и Виктор повторяют этапы (1) - (4) n раз.
Если Пегги не обманывает, она сможет предъявить Виктору одно из доказательств на этапе (3). Однако, если гамильтонов цикл для G ей неизвестен, она не сможет создать зашифрованный граф H', который удовлетворяет обоим доказательствам. Лучшее, что она может сделать - это создать или граф, изоморфный G, или граф с таким же числом точек и линий и правильным гамильтоновым циклом. Хотя ее шансы угадать, какое доказательство потребует Виктор на этапе (3), составляют 50 процентов, Виктор может повторить протокол достаточное число раз, убеждаясь, что Пегги знает гамильтонов цикл для G.
Параллельные доказательства с нулевым знанием
В базовом протоколе с нулевым знанием используется n обменов информацией между Пегги и Виктором. Почему бы не выполнить их параллельно:
(1) Пегги использует свою информацию и n случайных чисел для преобразования трудной проблемы в n различных изоморфных проблем. Затем она с помощью своей информации и случайных чисел решает n новых трудных проблем.
(2) Пегги вручает решение n новых трудных проблем.
(3) Пегги раскрывает Виктору эти n новых трудных проблем. Виктор не может воспользоваться этими новыми проблемами для получения информации об оригинальных проблемах или их решении.
(4) Для каждой новой трудной проблемы Виктор просит Пегги либо
(a) доказать ему, что старая и новая проблемы изоморфны, либо
(b) раскрыть решение, врученное на этапе (2), и доказать, что оно является решением данной новой проблемы.
(5) Пегги исполняет его просьбу для каждой новой проблемы.
К несчастью, все не так просто. Этот протокол, в отличие от предыдущего, не обладает такими же свойствами нулевого знания. На этапе (4) Виктор может потребовать, чтобы доказательство было представлено в виде значения однонаправленной хэш-функции всех значений, врученных на первом этапе, делая невозможным имитацию записи протокола. Это тоже нулевое знание, но другого рода. На практике оно представляется безопасным, но никто не знает, как это доказать. Мы действительно знаем только то, что при определенных условиях определенные протоколы для определенных проблем могут быть выполнены параллельно без потери свойства нулевого знания [247, 106, 546, 616].
Неинтерактивные доказательства с нулевым знанием
Кэрол невозможно убедить, потому что она не участвует в интерактивном процессе протокол. Для убеждения Кэрол и других заинтересованных лиц нам нужен неинтерактивный протокол.
Для неинтерактивных доказательств с нулевым знанием был придуман ряд протоколов [477, 198, 478, 197], которые не требуют непосредственного взаимодействия. Пегги может опубликовать их и, таким образом, доказать свое знание всем, у кого найдется время это проверить
Базовый протокол похож на параллельное доказательство с нулевым знанием, но место Виктора занимает однонаправленная хэш-функция:
(1) Пегги использует свою информацию и n случайных чисел для преобразования трудной проблемы в n различных изоморфных проблем. Затем она с помощью своей информации и случайных чисел решает n новых трудных проблем.
(2) Пегги вручает решение n новых трудных проблем.
(3) Пегги использует все эти вручения в качестве входа для однонаправленной хэш-функции. (В конце концов эти вручения - не что иное, как строки битов.) Затем она сохраняет первые n битов полученного значения однонаправленной хэш-функции.
(4) Пегги берет n битов, полученных на этапе (3). По очереди для каждой n-ой трудной проблемы она берет n‑ый бит и
(a) если бит равен 0, доказывает, что старая и новая проблемы изоморфны, либо
(b) если бит равен 1, раскрывает решение, врученное на этапе (2), и доказывает, что оно является решением данной новой проблемы.
(5) Пегги опубликовывает все решения, врученные на этапе (2), и все доказательства, полученные на этапе (4).
(6) Виктор, Кэрол и все остальные заинтересованные лица проверяют, что этапы (1)-(5) выполнены правильно.
Это впечатляет: Пегги может опубликовать некоторые данные, которые не содержат никакой информации о ее секрете, но могут кого угодно убедить в существовании самого секрета. Этот протокол может быть использован проверка определена как вычисление однонаправленной хэш-функции первоначальных сообщений и подписываемого сообщения.
Эта схема работает, потому что однонаправленная хэш-функция действует как беспристрастный генератор случайных битов. Чтобы мошенничать, Пегги нужно уметь предсказывать результат однонаправленной хэш-функции. (Помните, если решение трудной проблемы ей неизвестно, она может сделать на этапе (4) либо (a), либо (b), но не оба действия одновременно.) Если она каким-то образом узнает, выполнение какого действия потребует от нее однонаправленная хэш-функция, то она сможет смошенничать. Однако, Пегги не сможет заставить однонаправленную хэш-функцию выдать определенный бит или догадаться, какой бит будет получен. Однонаправленная хэш-функция по сути является заменителем Виктора в случайном выборе одного из двух доказательств на этапе (4).
В неинтерактивном протоколе должно быть гораздо больше итераций в последовательности запрос/ответ. Пегги, а не Виктор, отбирает трудные проблемы с помощью случайных чисел. Она может подбирать различные проблемы, следовательно, и различные векторы вручения, до тех пор, пока хэш-функция не выдаст что-то, нужное Пегги. В интерактивном протоколе 10 итераций - вероятность мошенничества Пегги составит 1 шанс из 210 (1 из 1024) - может быть достаточно. Однако, для неинтерактивных доказательств с нулевым знанием этого не хватит. Помните, что Мэллори всегда может выполнить на этапе (4) либо (a), либо (b). Он может, выполняя этапы (1)-(3), попытаться догадаться, что его попросят сделать, и посмотреть, правильно ли его предположение. Если нет, он попробует снова и снова. Сделать 1024 предположения на компьютере нетрудно. Для предотвращения такого вскрытия грубым взломом для неинтерактивных протоколов нужно 64 или даже 128 итераций.
Главная идея состоит в использовании однонаправленной хэш-функции - Пегги не может предсказать выход хэш‑функции, потому что она не может предсказать ее вход. Вручения, используемые на входе, становятся известны только после решения новых проблем.
Общие замечания
Блюм (Blum) доказал, что любая математическая теорема может быть преобразована в граф, такой, что доказательство теоремы будет эквивалентно доказательству существования гамильтонова цикла для этого графа. В общем виде то, что для любого NP-полного утверждения есть доказательство с нулевым знанием, использующее однонаправленные функции и, следовательно, хорошие алгоритмы шифрования, доказано в [620]. Любое математическое доказательство может быть преобразовано в доказательство с нулевым знанием. Используя эту методику, исследователь может доказать миру, что ему известно доказательство конкретной теоремы, не раскрывая самого решения. Блюм мог опубликовать свои результаты, не раскрывая их.
Также существуют доказательства с минимальным раскрытием [590]. Для доказательства с минимальным раскрытием выполняются следующие свойства:
Дата добавления: 2021-01-26; просмотров: 512;











