Гидравлический расчет сифонного трубопровода.

Сифон — это простой самотечный трубопровод, одна часть которого расположена выше свободной поверхности питающей его жидкости, а другая ниже.

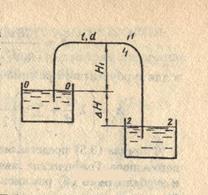
Жидкость движется в сифоне за счет разности уровней 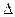Н. Заме­тим, чтобы началось движение по сифону, необходимо весь его объем заполнить жидкостью. Учтем, что для свободных поверхностей 0-0 и 2-2 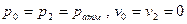и суммарное сопротивление склады­вается из потерь на трение по дли­не и местных, и запишем уравне­ние Бернулли:

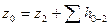
ИЛИ

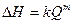
где 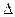Н представляет потребный (располагаемый) напор .

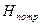Формула показывает, что расход жидкости через си­фон не зависит от высоты ее подъема 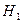. Однако при увеличе­нии 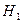давление жидкости 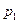снижается, вплоть до давления насыщенных паров, при котором в сечении 1-1 возникает кави­тация и расход уменьшается, вплоть до полного прекращения движения жидкости. Предельное значение 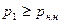рассчитыва­ется по уравнению Бернулли для участка 0-1.

Преобразуем уравнение к виду

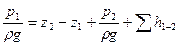
Потребным напором 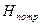для простого трубопровода назы­вается напор 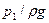в начальном сечении, обеспечивающий за­данный расход Q жидкости в трубопроводе.

Введя обозначение 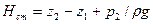перепишем в виде:

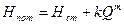
где 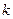и и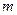меют разные значения в зависимости от режима тече­ния. Для ламинарного режима с учетом местных сопротивлений эквивалентными длинами имеем

,

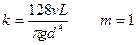а для турбулентного режима - .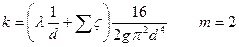

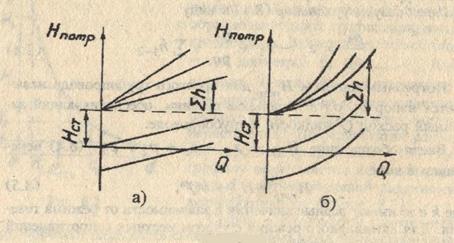
Формула представляет собой уравнение кривой потреб­ного напора. Графические зависимости 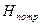для ламинарного (а) и турбулентного (б) режимов приведены на рис. Величина 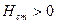, когда жидкость поднимается с меньшей высоты на боль­шую, и 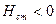при течении сверху вниз (при условии 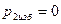). Крутизна кривых 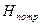зависит от коэффициента 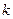и возрастает с увеличением длины трубопровода, с уменьшением диаметра, а также с увеличением местных гидравлических сопротивлений.

Иногда вместо кривых потребного напора удобнее пользо­ваться характеристикой трубопровода, под которой понимают зависимость суммарных потерь напора (или давления) в трубо­проводе от расхода 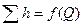. Таким образом, характерис­тика трубопровода представляет собой кривую потребного на­пора, смещенную в начало координат.