Действительные характеристики насоса.

Рабочие органы насоса рассчитывают для определения сочетания подачи, напора и частоты вращения, причём размеры и форму проточной полости выбирают так, чтобы гидравлические потери при работе на этом режиме были минимальными. Такое сочетание подачи, напора и частоты вращения называется расчётным режимом. При эксплуатации насос может работать на режимах, отличных от расчётного. Так, прикрывая задвижку, установленную на напорном трубопроводе насоса, уменьшают подачу. При этом также изменяется напор, развиваемый насосом. Для правильной эксплуатации насоса необходимо знать, как изменяются напор, КПД и мощность, потребляемая насосом, при изменении его подачи, т.е. знать характеристику насоса, под которой понимается зависимость напора, мощности и КПД от подачи насоса при постоянной частоте вращения.

Действительный напор насоса будет меньше теоретического вследствие конечного числа лопастей и затрат энергии жидкости на преодоление гидравлических сопротивлений в самом насосе.

Влияние первого фактора проявляется в неравномерном распределении скоростей в сечениях межлопастных каналов, что приводит к уменьшению напора, развиваемого насосом. Конечное число лопастей учитывается введением поправочного коэффициента k_Z<1: H_TZ = k_ZH_T∞ , где H_TZ- теоретический напор насоса с конечным числом лопастей. Среднее значение коэффициента k_Z=0,8.

Потери напора ∆H_Г на преодоление гидравлических сопротивлений внутри насоса учитываются гидравлическим к.п.д. η_г, величина которого зависит от конструкции насоса и режима его работы и колеблется в пределах 0,85÷0,95.

Таким образом, действительный напор, развиваемый насосом,

H_H = H_TZ-∆H_Г = η_ГH_TZ = k_Z η_ГH_T∞, или H_H = k_Z η_Г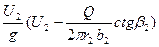

На рис. Показан переход от напорной характеристики идеального насоса H_T∞ = f(Q) к характеристике реального насоса H_H = f(Q_H), основанный на приведённых рассуждениях.

Подача насоса Q_H отличается от расхода Q через рабочее колесо на величину утечек ∆Q_У, что учитывается объёмным к.п.д. насоса η₀:

Q_H = Q-∆Q_У = η₀Q. Учёт утечек приводит к сдвигу действительной напорной характеристики насоса H_H = f(Q_H) относительно кривой H_H = f(Q) влево на величину ∆Q_У.

Построим кривую мощности насоса. Гидравлическая мощность насоса (мощность, сообщаемая жидкости в рабочем колесе без учёта объёмных и гидравлических потерь) равна N_Г = ρqQH_TZ. Зависимость теоретического напора H_TZ от расхода через рабочее колесо линейная и может быть выражена уравнением H_TZ = A-BQ (рис.2.5). Отсюда гидравлическая мощность N_Г = ρq(AQ-BQ²). Это уравнение параболы, пересекающей ось абсцисс в точках Q=0 и Q=A/B (кривая N_Г = f(Q) на рис.2.6 ).

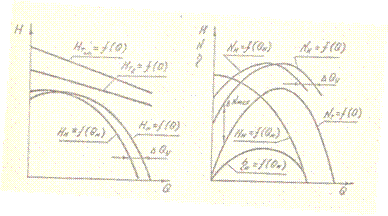
рис.2.5 рис.2.6

Прибавив мощность механических потерь ∆N_МЕХ к гидравлической мощности, получим кривую N_H = f(Q) зависимости мощности на валу насоса от расхода жидкости через рабочее колесо. Для получения характеристики насоса N_H = f(Q) остаётся учесть объёмные потери. Для этого кривую N_H = f(Q) нужно сместить влево на величину утечек ∆Q_У. Из рис. Видно, что минимальная потребляемая мощность соответствует режиму насоса при Q=0, поэтому пуск центробежного насоса производится при закрытой задвижке на напорном трубопроводе, чтобы уменьшить пусковую мощность приводящего двигателя.

Имея кривые N_H = f(Q) и H_H = f(Q_H), построим кривую η_H = f(Q_H) по уравнению η_H = ρgQ_HH_H/N_H. При Q_H=0 и H_H=0 → η_H=0. Следовательно, кривая к.п.д. пересечёт ось абсцисс в начале координат (Q_H=0) и в точке, где её пересекает кривая напора.

Данные рассуждения являются приближёнными, так как не учитывают ряда факторов, влияющих на напор и мощность. Поэтому характеристики насоса, построенные теоретически на основе описанных формул, плохо согласуется с данными опыта. С достаточной для практики точностью характеристики насоса могут быть получены лишь опытным путём.

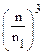
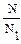
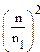
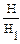
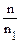
Характеристика центробежного насоса представляет графическое изображение зависимости напора Н , мощности N, к.п.д. η и допускаемой вакуумметрической высоты всасывания Нвак от подачи насоса Q при постоянных значениях частоты вращения РК n и плотности Ж на входе в насос. При другой частоте вращения РК n1 характеристика насоса может быть пересчитана по формулам :

= , = , =

.

На рис.2.7 приведены кривые связи H-Q и N-Q при различной частоте вращения РК, называемые универсальными или топографическими характеристиками. Кроме того, на рисунке нанесены кривые напора Н

( нисходящие линии ) и мощности N ( восходящие линии ) в функции от подачи Q. С помощью таких графиков можно для данной марки насоса выявить значения Q, H, N и η при различной частоте вращения РК.

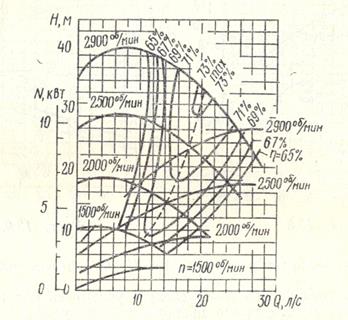
рис.2.7