Взаимное положение точки и прямой
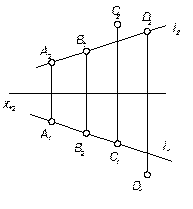
| т.А лежит на прямой т.В не лежит (III четверть) т.С выше прямой т.D перед прямой |
Если точка лежит на прямой, то её проекции лежат на одноимённых проекциях прямой.
1. Взаимное положение двух прямых
2 прямые в пространстве могут быть:
а) //,
б) пересекаться,
в) скрещиваться.
Если две прямые //, то их одноимённые проекции также //-ы друг другу.
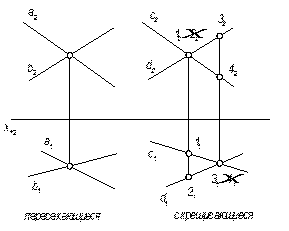
Если две прямые пересекаются:
Одноимённые проекции двух пересекающихся прямых пересекаются и точки их пересечения лежат на одной линии связи. В противном случае прямые скрещиваются.
2. Проекции плоскостей. Способы задания и изображения плоскости на комплексном чертеже
Определителем плоскости называется совокупность геометрических элементов, однозначно задающих положение плоскости в пространстве.
На комплексном чертеже плоскость задаётся проекциями элементов своего определителя.
Способы задания плоскостей:
1) тремя точками, не лежащими на одной прямой
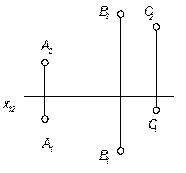 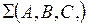
|
2) прямой и точкой, не лежащей на этой прямой
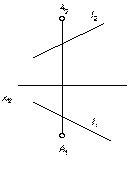 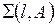
|
3) двумя пересекающимися прямыми
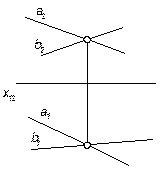 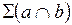
|
4) двумя параллельными прямыми
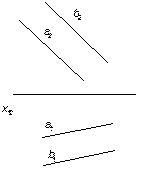 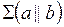
|
5) любой плоской фигурой
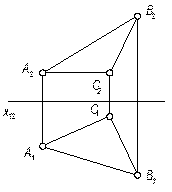 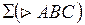
|
Мы рассмотрим способы задания плоскости общего положения.
Плоскость считается заданной, если относительно любой точки пространства можно однозначно решить задачу о её принадлежности к этой плоскости.
3. Плоскости частного положения
К плоскостям частного положения относятся // или ^ к какой-либо плоскости проекций.
Плоскость, ^ плоскости проекций, называется проецирующей плоскостью.
^ к П1 – горизонтально проецирующая,
^ к П2 – фронтально проецирующая,
^ к П3 – профильно проецирующая.
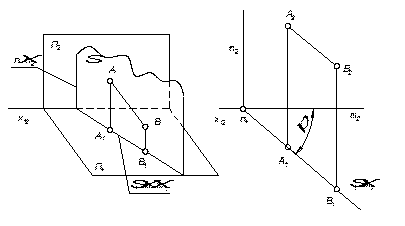
горизонтально-проецирующая 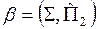
Горизонтальные проекции всех точек, линий и фигур, лежащих в плоскости, проецируются на горизонтальную проекцию плоскости – собирательное свойство плоскости.
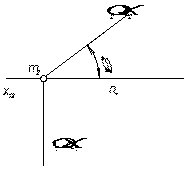 фронтально-проецирующая
фронтально-проецирующая 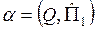
|
Плоскость, // плоскости проекций, называется плоскостью уровня.
// П1 – горизонтальная плоскость уровня,
// П2 – фронтальная плоскость уровня,
// П3 – профильная плоскость уровня.
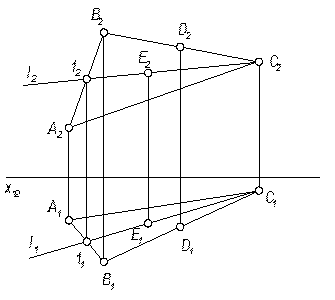
4. Точка в плоскости
Точка лежит в плоскости, если она принадлежит прямой, лежащей в этой плоскости.
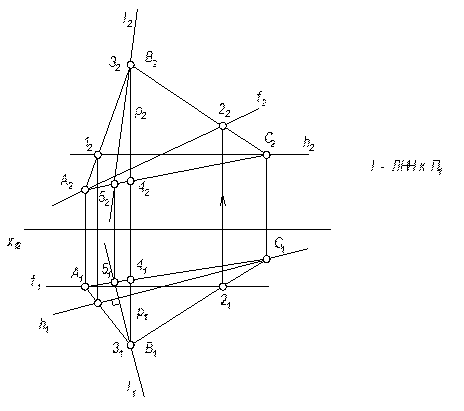
5. Линии в плоскости
Среди множества прямых, лежащих в плоскости общего положения, можно выделить прямые частного положения.
Через любую точку плоскости общего положения всегда проходит 1 горизонталь, фронталь и профильная прямая уровня.
6. Параллельность прямой и плоскости
Прямая // плоскости, если в плоскости можно провести прямую, // данной.
1) Чаще всего приходится отвечать на вопрос: параллельны ли между собой заданная плоскость и прямая. Для этого на одной проекции плоскости проводится проекция прямой // проекции заданной прямой. Затем, из условия принадлежности прямой плоскости строится её вторая проекция и определяется, параллельна ли она второй проекции заданной прямой.

| 1) 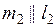 2)
2) 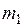 не не 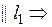 m не
m не 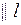 и
l не и
l не  АВС АВС
|
2) построить прямую, // данной плоскости

| например,
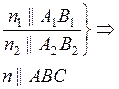 Задача имеет
Задача имеет  решений решений
|
1) через заданную точку провести плоскость // данной прямой
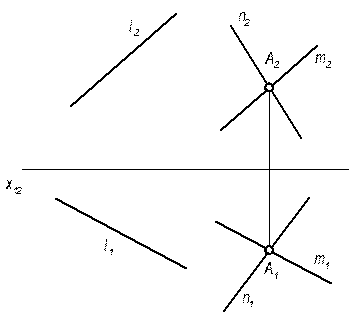
| 1) m||l Q(m,n)||l |
7. Параллельность плоскостей
Плоскости параллельны друг другу, если 2 пересекающиеся прямые одной плоскости //-ы двум пересекающимся прямым другой плоскости.
1) через заданную точку провести плоскость // данной.
2) заданы 2 плоскости, надо определить параллельны ли они между собой.
8. Классификация многогранников
Многогранником называется тело, ограниченное плоскими многоугольниками.
Многогранник называется выпуклым, если весь он лежит по одну сторону от плоскости любой его грани.
Многогранник называется правильным, если его боковые грани являются правильными многоугольниками.
Платон открыл 5 правильных выпуклых многогранников:
1) тетраэдр (четырёхгранник) – правильная треугольная пирамида;
2) гексаэдр(куб) – 8 вершин, 6 граней – квадратов;
3) октаэдр(8ми-гранник) – 6 вершин, 8 граней – треугольников;
4) икосаэдр(20ти-гранник) – 12 вершин, 20 граней – треугольников;
5) додекаэдр(12ти-гранник) – 20 вершин, 12 граней – пятиугольников.
Среди неправильных многогранников наибольший интерес представляют:
1) призмы – боковые рёбра // друг другу, а боковыми гранями являются параллелограммы;
2) пирамиды - боковые рёбра пересекаются в одной точке вершины;
3) призматоиды– многогранники, ограниченные какими-либо двумя многоугольниками, расположенными в //-ных плоскостях, называемыми основаниями, и треугольниками или трапециями, вершинами которых служат вершины оснований.
9. Изображение многогранников на комплексном чертеже
Многогранник на комплексном чертеже изображается проекциями своих вершин и рёбер.
Для придания однозначности чертежу вершины необходимо пронумеровать, а рёбра обвести с учётом видимости. Для определения видимости рёбер надо воспользоваться конкурирующими точками.
10. Понятие о поверхности
В математике под поверхностью понимается непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая в декартовой системе координат уравнением вида F(x,y,z)=0.
Дата добавления: 2016-10-26; просмотров: 4584;











