Используя понятия «множество» и «точка» можно дать следующее определение: поверхностью называется непрерывное двухпараметрическое множество точек.

11. Способы задания поверхностей

Поверхность считается заданной, если относительно произвольной точки пространства можно однозначно решить вопрос о её принадлежности данной поверхности.

Для поверхности, заданной на чертеже, это условие становится следующим: поверхность считается заданной, если по одной проекции точки, принадлежащей поверхности, можно построить вторую проекцию точки.

Совокупность условий, необходимых для задания поверхности, называется определителем поверхности. Он состоит из геометрической и алгоритмической частей.

Геометрическая часть определителя – перечень геометрических элементов и фигур, которые участвуют в образовании поверхности.

Алгоритмическая часть определителя описывает взаимосвязи между элементами и фигурами, входящими в геометрическую часть, а также составляет совокупность правил, по которым образуется поверхность.

Иногда вместо алгоритмической части задаются параметры поверхности, которые делятся на параметры формы и параметры положения.

Существуют следующие способы задания поверхности:

1) аналитический – поверхность рассматривается как ГМТ, координаты которых удовлетворяют уравнению заданного вида:

F(x,y,z)=0

z=f(x,y)

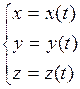- параметрическое задание

Главный недостаток – не наглядность,

Достоинство – удобно использовать для моделирования поверхностей на ЭВМ.

2) графический– поверхность задаётся на чертеже проекциями элементов своего определителя и некоторыми наиболее характерными линиями (типа очерк поверхности).

Очерк поверхности – линия, отделяющая проекции поверхности от остальной части плоскости проекций.

3) графоаналитический –часть линий аналитически, часть – графически: например, образующая - графически, направляющая – аналитически (линии – параметроносители).

12. Классификация поверхностей

Поверхности классифицируются по двум признакам:

1) по виду образующей линии

2 класса:

а) линейчатые – образующая - прямая;

б) не линейчатые – образующая – кривая;

2) по виду движения образующей линии:

а) поверхности плоскопараллельного переноса – образующая совершает поступательные движения;

б) поверхности вращения;

в) винтовые поверхности.

13. Поверхности вращения

Поверхностью вращения называется поверхность, образуемая при вращении некоторой линии вокруг неподвижной оси.

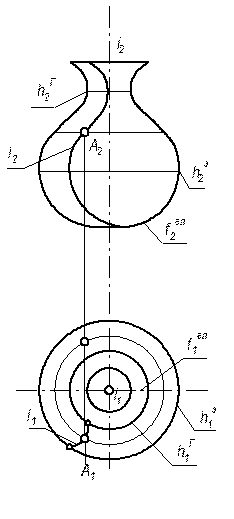
Каждая точка образующей при своём вращении будет описывать окружности, плоскости которых ^ к оси вращения. Такие окружности называются параллели. Самая большая параллель – экватор, самая маленькая – горло.

Если поверхность вращения рассекать плоскостями, проходящими через ось вращения, то в сечении будут лежать кривые, называемые меридианами. Все меридианы равны между собой, но меридиан, лежащий в плоскости уровня, называется главным.

Очерком поверхности вращения на одной плоскости проекций служит главный меридиан, а на другой – экватор и горло.

Чтобы построить точку, лежащую на поверхности вращения, нужно сначала взять вспомогательную линию на поверхности (лучше параллель) и расположить проекции точки на одноимённых проекциях вспомогательной линии.