Резонанс напряжений

Резонанс в цепи с последовательным соединением источника энергии и реактивных элементов L и C получил название резонанса напряжений. Про­стейшая схема такой цепи по­казана на рис. 59.

Комплексное входное сопротивление схемы: .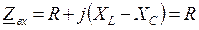

Условие резонанса напряжений: X_э= X_L - X_C или wL = 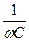, откуда w₀ = 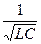- ре­зонансная или собственная частота.

Из полученного равенства следует, что резонансного режима в цепи можно достичь изменением параметров элементов L и C или частоты источника w.

В резонансном режиме полное сопротивление схемы имеет минимальное значение и равно активному сопротивлению:

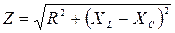= R,

а ток максимален и совпадает по фазе с напряжением источника: I=E/R; j = 0.

Векторная диаграмма напряжений и тока показана на рис. 60.

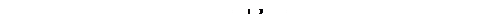
Напряжения на реактивных элементах равны по модулю, противопо­ложны по фазе и взаимно компенсируют друг друга:

; ,

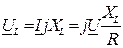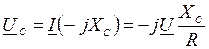а напряжение на резисторе равно напряжению источника : U_R=IR=U=E.

Равные по модулю напряжения на реактивных элементах U_L=U_C = 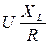могут зна­чи­тельно превосходить напряжение источника U = Е при условии, что X_L=X_C>>R.

Выясним энергетические процессы, протекающие в цепи в резонансном режиме. Пусть в цепи протекает ток i =I_msinwt, тогда напряжение на конденса­торе составит:

.

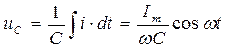Сумма энергий магнитного и электрического полей равна:

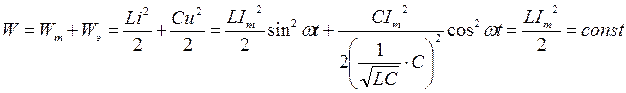
Таким образом, сумма энергий магнитного и электрического полей равна постоян­ному значению. Это значит, что между магнитным и электрическим по­лями происходит не­прерыв­ный обмен энергией, суммарное значение которой постоянно, а обмен энергией ме­жду ис­точником и цепью отсутствует, при этом поступающая от источника энергия преобра­зуется в другие виды..

Электрическая цепь с последовательным соединением элементов R, L, C в технике по­лучила название последовательного колебательного контура. Свой­ства такой цепи как ко­ле­бательного контура характеризуют следующие пара­метры: 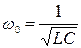- резонансная частота; r = 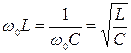- волновое со­противле­ние; Q = 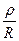- добротность.

Чем больше добротность контура Q, тем выразительнее проявляются в нем резо­нанс­ные явления; например, напряжения на реактивных элементах больше напряжения ис­точника в Q раз: U_L = U_C = UQ.

При изменении частоты источника w = var будут изменяться сопротивле­ния реак­тив­ных элементов и, как следствие, будут изменяться ток в цепи и на­пряжения на отдельных участках.

Частотными характеристиками контура называются зависимости сопро­тивлений от­дельных элементов и участков от частоты X_L =wL; X_C = 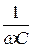; X =X_L-X_C ; Z= 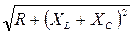(рис. 61).

Резонансными характеристиками называются зависимости режимных па­раметров от частоты: U_L, U_C, I, j = f(w)(рис. 62).

Полосой пропускания резонансного контура называют область частот Dw = w₁-w₂, на границах которой ток I в 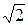раз меньше своего максимального значения, т.е^. I=0,707I_max. Полоса пропускания контура обратно пропорцио­нальна его добротности: Dw = 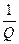. На рис. 63 в относительных единицах пред­ставлено семейство резонансных характеристик с различ­ными значениями доб­ротности.

Резонанс токов

Резонанс в цепи с параллельным соединением источника энергии и ре­активных эле­ментов L и C получил название резонанса токов. Простейшая схема такой цепи показана на рис. 64.

Комплексная входная проводимость схемы:

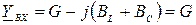
Условие резонанса токов: 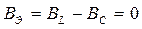или 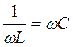, откуда 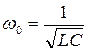- резо­нансная (собственная) частота.

Из полученного равенства следует, что резонансного режима в цепи можно достичь изменением параметров элементов L и C или частоты источ­ника w.

В резонансном режиме полная проводимость схемы равна активной про­водимости и имеет минимальное значение: 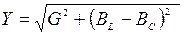= G, а ток ис­точника также минима­лен и совпадает по фазе с напряжением источника ( j = 0): I =UY = UG.

Токи в ветвях с реактивными элементами I_L=U(-jB_L), I_C =U(jB_C) равны по модулю, противоположны по фазе и компенсируют друг друга, а ток в рези­сторе G равен току источ­ника (I=I_G=UG). Равные по модулю токи в реактивных элементах I_L = I_C могут значительно превосходить ток источника I при усло­вии, что B_L=B_C>>G .

Векторная диаграмма токов и напряжений показана на рис. 65.

Электрическая цепь с параллельным соединением элементов G, L и C в технике по­лу­чила название параллельного колебательного контура. Свойства такой цепи как колеба­тель­ного контура характеризуют следующие параметры: 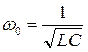- резонансная частота; 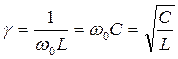- волновая проводи­мость; 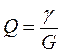- добротность.

Резонансные характеристики параллельного контура представлены на рис. 66.