Плазма в природе и в лаборатории

Что такое плазма ?

Плазма - это ионизованный газ. Таково, пожалуй, самое общее и самое неточное определение плазмы. Возможно, однако, что оно и самое правильное, по крайней мере, для начала. Ведь все уточнения приведенного определения связаны со свойствами, присущими этой квазинейтральной смеси заряженных и нейтральных частиц, обладающей коллективными степенями свободы во взаимодействии заряженных частиц. Действительно, уже в этом первом качественном уточнении содержатся два понятия, нуждающиеся в объяснении. Объяснения мы попытаемся дать чуть позже, а пока приведем еще одно описательное высказывание, намечающее место нашего предмета в привычной для нас картине мироздания и обычно используемое в популярной литературе.

При нагревании вещества его состояние изменяется с достижением некоторых критических температур: из твердого состояния оно переходит в жидкое (при температуре плавления), затем (при температуре испарения) – в газообразное. Если газ нагревать и дальше, то в нем будет появляться все более заметное количество ионов и электронов – заряженных частиц, образующихся при ионизации атомов (молекул). При достаточно высоких температурах практически все атомы (молекулы) газа могут оказаться ионизованными. Так что плазму можно интерпретировать как следующее (четвертое) состояние вещества. Поскольку при ионизации атома (молекулы) образуется пара: ион и электрон, естественно считать, что полные количества положительных и отрицательных зарядов во всем рассматриваемом объеме, занятом нагреваемым веществом, равны. Сохранение такого равенства на уровне элементарного объема и называется квазинейтральностью плазмы. Заряженные частицы, составляющие плазму, создают вокруг себя электрическое поле, обеспечивающие их кулоновское (т.е. достаточно дальнодействующее) взаимодействие друг с другом. Каждая из частиц испытывает при этом воздействие большого числа окружающих ее кулоновских центров, двигаясь в суммарном электрическом поле и внося свой вклад в воздействие на остальные. Такая коллективность является характерной чертой поведения плазмы.

Плазма в природе и в лаборатории

Понятие “плазма” в смысле, употребленном в предыдущем параграфе, появилось в физике сравнительно поздно – в двадцатых годах закончившегося двадцатого столетия. И это при том, что, как теперь часто можно слышать, 99% обычного вещества (не считая упоминаемой в последнее время «темной материи») во Вселенной находится именно в плазменном состоянии. Звезды и их атмосферы, газовые туманности и межзвездный газ, солнечный ветер и радиационные пояса “Земли” – все это плазма с большей или меньшей степенью ионизации. Однако условия зарождения и развития жизни, по крайней мере, в той ее форме, частью которой является Человечество, далеки от условий существования плазмы. Действительно, если рассмотреть “комнатные” условия: плотность нейтральных атомов n₀ ~ 3 10²⁵ м³ ; T ~ 300 ⁰K , то, с помощью формулы Саха (вывод которой будет приведен в параграфе 1.7), можно вычислить степень ионизации газа, находящегося в тепловом равновесии:

n_i/n₀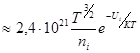

U_I – энергия ионизации для азота – равна 14,5 эВ и степень ионизации в этом случае получается на уровне 10^-122 , что является пренебрежимо малой величиной. Лишь при таком увеличении температуры газа, что KT приближается к U_I , содержание ионов в нем становится заметным и, при дальнейшем росте температуры газ, в конце концов, превращается в практически полностью ионизованную плазму.

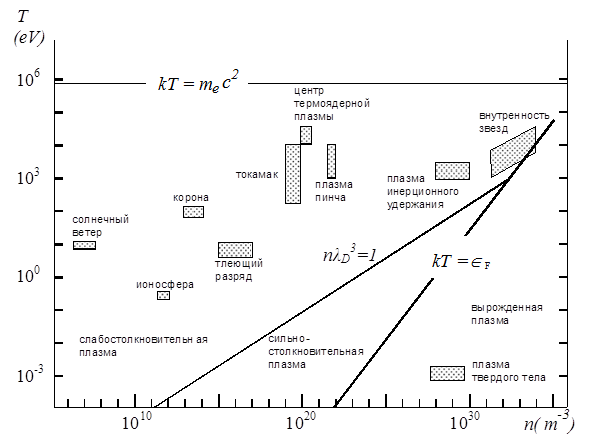
Рис. 1.1.Различные области параметров плазмы с их привязкой к природным и лабораторным условиям.

На рисунке 1 представлена диаграмма в координатах n – T, демонстрирующая характерные значения этих параметров для различных природных и лабораторных условий существования плазмы.

1.3. Квазинейтральность и масштабы разделения зарядов.

Квазинейтральность плазмы

Итак квазинейтральность плазмы - это приблизительное равенство плотностей положительных и отрицательных зарядов в плазме. Степень этой приблизительности, а следовательно и точность этого определения также нуждаются в дальнейшем обсуждении.

Обсуждение понятия квазинейтральности удобно начать с рассмотрения последствий, к которым привело бы ее нарушение. Итак, представим себе крайний случай: заряды одного знака в некотором единичном объеме каким-то образом исчезли, и этот объем оказался заряженным оставшимися зарядами противоположного знака. Если это сферический объем радиуса 1мм и был он заполнен газом при нормальных условиях, то полное число частиц N ~ (4/3) pr³ (A/U_m) составит величину ~ 10¹⁷ частиц.(A – число Авогадро, U_m – молярный объем). Если каждая из частиц будет заряжена единичным зарядом, то полный заряд, сосредоточенный в такой сфере окажется ~4.8 10⁷ единиц заряда CGSE или 1.6 10^-2 кулона. Энергия такой заряженной сферы составила бы величину ~ 10⁹ джоулей, что примерно эквивалентно энергии, содержащейся в 100 килограммах тротила. Энергетическая «невыгодность» нарушения квазинейтральности становится, таким образом, достаточно наглядной.

Дебаевский радиус и ленгмюровская частота

Приблизительность сохранения нейтральности обусловлена наличием теплового движения частиц, составляющих плазму. Действительно, будучи случайным, тепловое движение приводит к флуктуациям плотности частиц и, соответственно, зарядов. В связи с этими флуктуациями возникают локальные нарушения квазинейтральности. Оценить пространственный и временной масштабы такого локального “разделения зарядов” можно на простом примере образования “плоского” двойного слоя. Пусть в каком-то месте произошло относительное смещение ионной и электронной компонент плазмы вдоль оси хна расстояние d. Получилось что-то вроде плоского конденсатора с расстоянием между обкладками, равным d, и поверхностной плотностью заряда s ~ n× e× d. Из курса общей физики известно, что напряженность поля в плоском конденсаторе E = 4p s, что дает разность потенциалов между его обкладками U = 4p s × d. Потенциальная энергия каждой из частиц, составляющих двойной слой, равна eU. Поскольку само рассматриваемое разделение зарядов произошло из-за теплового движения частиц, мы должны приравнять изначальную кинетическую энергию частицы (~T)приобретенной в результате разделения зарядовпотенциальной энергии: T~4pn× e²× d².Из полученного соотношения следует оценка для характерного пространственного масштаба разделения зарядов :

d ~ (T /4p n× e²)^1/2

Эта величина носит название дебаевской длины или дебаевского радиуса.

Очевидно, что возникшее разделение зарядов приведет к силам, возвращающим заряженные частицы в “исходное состояние” – потенциальная энергия будет вновь переходить в кинетическую. Характерное время, за которое “рассосется” возникший объемный заряд может также быть оценено из простых соображений. Частицам нужно пройти расстояние порядка d, при этом их скорости определяются той же тепловой энергией: u_T ~ (T /m)^1/2 . Разделив d на U_T, получим t ~(m/4p n× e²) ^1/2. Обратная этому времени величина, имеющая размерность частоты: w₀ ~ (4p n× e²/m) ^1/2 . Эта частота носит название ленгмюровской частоты и характеризует временной масштаб разделения зарядов в плазме.

Поле точечного заряда в плазме

Более строгий подход к введению понятия характерного пространственного масштаба разделения зарядов в реализуется при рассмотрении поля точечного заряда в плазме.

Запишем уравнение Пуассона для точечного заряда e_a ,находящегося в окружении плазмы, состоящей из положительных однозарядных ионов и электронов, имеющих Больцмановское распределение плотности и одинаковую температуру T:

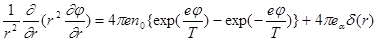(1.3.1)

Введем новую переменнуюc = r j , и будем рассматривать область вне точки r = 0,считая также, что ej/T << 1. Это дает нам возможность, ограничившись в разложении экспонент линейными членами, переписать (1.3.1) в более удобном виде:

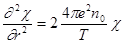(1.3.2)

Если величину, стоящую перед c в правой части выражения(1.3.2) обозначить как 1/d², то оно будет выглядеть еще более компактно:

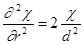(1.3.3 )

Величина 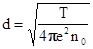, совпадает с выражением для Дебаевского радиуса, полученным нами ранее оценочно.

Решение уравнения (1.3.3) записывается в виде c = Cexp{-r/d}или, с учетом введенного обозначения для c

j =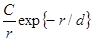

Постоянная С должна быть выбранатак, чтобы при r®0 выражение для потенциала стремилось к таковому для вакуумного случая 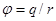. Таким образом имеем окончательно:

j = 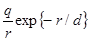(1.3.4)

Это выражение для экранированного потенциала, возникающего около заряда, окруженного плазмой. С позиции проведенного рассмотрения Дебаевский радиус трактуется как характерное расстояние экранирования точечного заряда в плазме.