Статистический контроль доли дефектных изделий

Рассмотрим случай, когда контролю подвергается партия изделий достаточно большого объема N.Все Nизделий, входящих в партию, по некоторому признаку делятся на две группы; кондиционные и дефектные.

Пусть число дефектных изделий в партии равно М.

Обозначим через S долю дефектных изделий в партии

S = 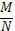(1)

По величине S1 партия изделий может быть разделена на 3 категории:

1) S ≤S₁,

2) S₁< S <S₂,

3) и с S≥ S₂

Величины S₁ и S₂ устанавливаются по соглашению между поставщиком изделий и их потребителем.

При статистическом контроле доли дефектных изделий делается случайная выборка в пизделий из партии и определяется число тдефектных изделий в выборке. Тогда доля дефектных изделий в выборке будет

S = 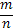(2)

В дальнейшем будем рассматривать только случаи, когда пмало ло сравнению с N (n < 0,1N),

В этих случаях можно принять, что случайная величина тимеет биномиальное распределение.

Если еще S мало по сравнению с 1 (S < 0,1), то можно принять, что случайная величина m имеет распределение Пуассона.

В настоящей главе рассматривается статистический контроль доли дефектных изделий в двух вариантах:

1) распределение m пуассоновское;

2) распределение m биномиальное.

Заметим, что в обоих вариантах математическое ожидание числа дефектных изделий в выборке будет равно

α = nS, (3)

При статистическом контроле доли дефектных изделий обычно в технических условиях задается норматив с таким образом, что при условии

m ≤ с, (4)

партия изделий оценивается удовлетворительно (принимается). В случае, когда

m > с, (5)

партия изделий оценивается неудовлетворительно (бракуется).

Для организации статистического контроля необходимо выбрать объем выборки при оценочный норматив с. Этот выбор делается с учетом риска поставщика и риска потребителя.

Риском поставщика называется вероятность α того, что партия первой категории с S = S1будет в результате испытаний оценена неудовлетворительно

α=Вер(m > с, при S = S₁). (6)

Из уравнения (6) видно, что α - это наибольшая вероятность получить условие (5) для партий первой категории, так как при S < S₁риск поставщика будет меньше, чем при S= S₁.

Риском потребителя называется вероятность α того, что партия третьей категории с S = S₂ будет в результате испытаний оценена удовлетворительно

β= Вер(m≤с при S = S₂). (7).

Из уравнения (7) видно, что β - это наибольшая вероятность получить условие (4) для партий третьей категории, так как при S > S₂ риск потребителя будет меньше, чем при S = S₂ .

Рациональная организация статистического контроля заключается в выборе n и таким образом, чтобы риск α и β были достаточно малы. Решение этой задачи приводится в следующем параграфе.