Расширенная постановка задачи

В то же время, спрос и предложение могут быть существенно разнесены не только в пространстве, но и во времени: например, спрос на отопительный уголь возникает лишь в зимний период (пиковый спрос), в то время как по технологическим соображениям его целесообразно добывать равномерно весь год, тем самым обеспечивая его равномерное предложение. Урожай, с другой стороны, собирают в летний период (пиковой предложение), а произведенную из собранного зерна муку потребляют равномерно в течение года. Хотя годовые объемы спроса и предложения в обоих случаях равны друг другу, локальные временные различия обуславливают необходимость хранения продукта (товара, груза) в той или иной локации – у производителя, у потребителя, или, как будет показано далее, в самой системе перевозки. Иными словами, в двух приведенных выше примерах наличие склада и запаса продукта на нем являются объективной необходимостью для обеспечения второго требования логистики: наличия продукта в нужное время. Эта же необходимость возникает при доставке грузов (точнее товаров, еще точнее – продуктов) с разной степени сезонности или рыночной востребованности.

Третье требование логистики, а именно обеспечение продукта в нужном объеме, для своего удовлетворения также требует наличие складов. Это объясняется необходимостью накапливать на них объемы поступающих от производителя грузов для формирования транспортных партий, размер которых устанавливается экономическими требованиями перевозчика. Грузы от производителя поступают относительно равномерно, и по достижении определенного объема разово вывозятся из точки А в точку В в составе единой транспортной партии. Поступление грузов от производителей в точку А и распределение доставленных перевозчиком в точку В грузов потребителям так же составляют свою равную по значимости часть общей грузовой транспортной системы. На рис. 5 в самом упрощенном виде показана система транспортировки подобного рода.

Рисунок 34 - Пример простейшей системы транспортировки

На этом рисунке продукт производится в локациях a1, a2, a3 и доставляется в точку A. Из точки А собранная партия продукта доставляется в точку В, откуда распределяется потребителям в локациях b1, b2, b3.

Представление системы транспортировки в виде части плоскости позволяет составить представление о пространственных аспектах работы грузовой транспортной системы. В то же время, в локациях a1, a2, a3 продукты могут производиться в разное время, что потребует хранения в точке A грузов, прибывших ранее, в ожидании момента накопления транспортной партии. То же может происходить и в точке В: перемещенные в нее грузы могут оказаться доставленными слишком рано для потребителей в локациях b1, b2, b3, что приведет к необходимости хранения грузов в точке В для синхронизации спроса на них.

Кроме того, имеется еще один важный аспект: покинувший исходную локацию груз не прибывает мгновенно в точку назначения, находясь некоторое время в процессе перемещения. Это объем груза, называемый обычно «запас в пути» (stockonwheel), может составлять весьма значительные величины: например, десять контейнеровозов класса «Панамакс» на пути в некоторый порт могут везти в него 20 000 контейнеров, в то время как на складе порта единовременно будет находится лишь половина этого количества.

На рис. 6 условно детализированы не только перемещения груза между различными точками показанного на рис. 5 пространства, но и «расписание» этих перемещений в дискретном времени.

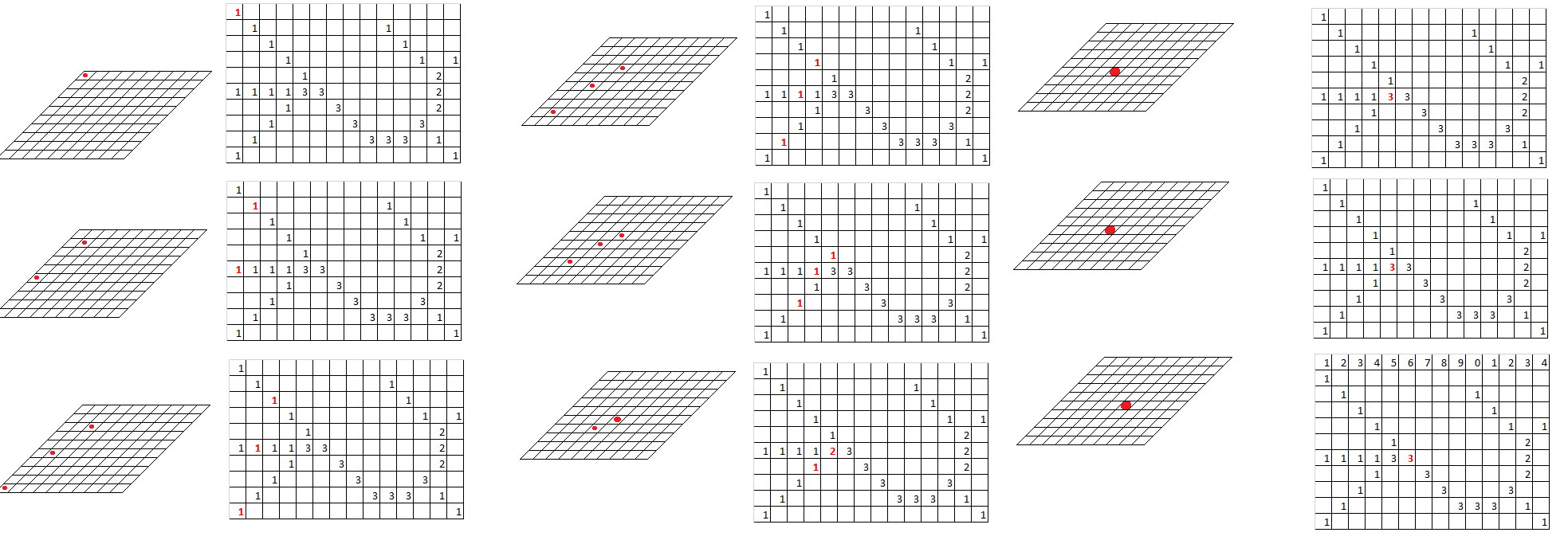
Рисунок 35 - Пример простейшей пространственной системы транспортировки

Каждая таблица на этом рисунке соответствует одному условному дискретному моменту времени. Иными словами, транспортировка в таком представлении является перемещением груза между различными точками в трехмерном пространстве {X, Y, t}, где X и Y являются пространственными координатами, а t в дискретном виде представляет время.

На рис. 7 условно показано функционирование упрощенной грузовой транспортной системы нашего примера в этом пространстве.

Рисунок 36 - Функционирование грузовой транспортной системы в пространстве {X,Y,t}

Поскольку мы обычно не рассматриваем перемещение по поверхности Земли в отдельных координатах {X, Y}, а так же из соображений наглядности, можно рассматривать функционирование грузовой транспортной системы в некотором условном пространстве {S, t}, где S – это расстояние перемещения в пространстве S=S(X,Y). Пример такого представления для одной простейшей транспортировки между двумя точками показан на рис. 8.

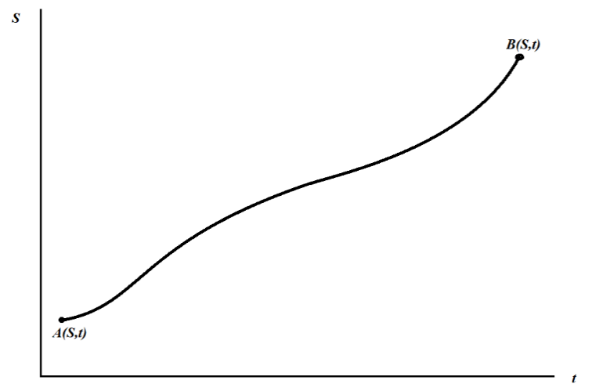
Рисунок 37 - Рассмотрение грузовой транспортной системы в координатах пространство-время

На этом рисунке функционирование некоторой простейшей грузовой транспортной системы показано как зависимость пройденного пути от времени, т.е. S=S(t). Очевидно, что величина 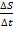(производная по времени) есть скорость перемещения груза в этой системе.

В то же время, функционирование этой системы может быть с таким же основанием рассмотрено как зависимость времени от пройденного пути, или t=t(S), что показано на рис. 9.

Рисунок 38 - Рассмотрение грузовой транспортной системы в координатах время- пространство

В этом случае величина 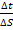(производная по расстоянию) есть задержка перемещения груза по маршруту, которая является такой же объективной характеристикой функционирования системы.

При этом задержка одновременно характеризуется как складированием (или «перемещением с нулевой скоростью», как говорят многие специалисты по логистике), так и собственно перемещением груза между исходной и конечной точкой, когда последний находится в пути между ними. Эти два случая в пространственном представлении различаются тем, что при собственно складировании соответствующая траектория ортогональна плоскости пространства (рис. 10), т.е. коллинеарна оси времени.

Рисунок 39 - Перемещение и складирование как компоненты транспортировки

Из этого рисунка видно, что традиционная постановка задачи выбора оптимального маршрута есть не более чем проекция всей схемы транспортировки в пространственно-временном континууме (рис. 10) на плоскость физического пространства (рис. 11).

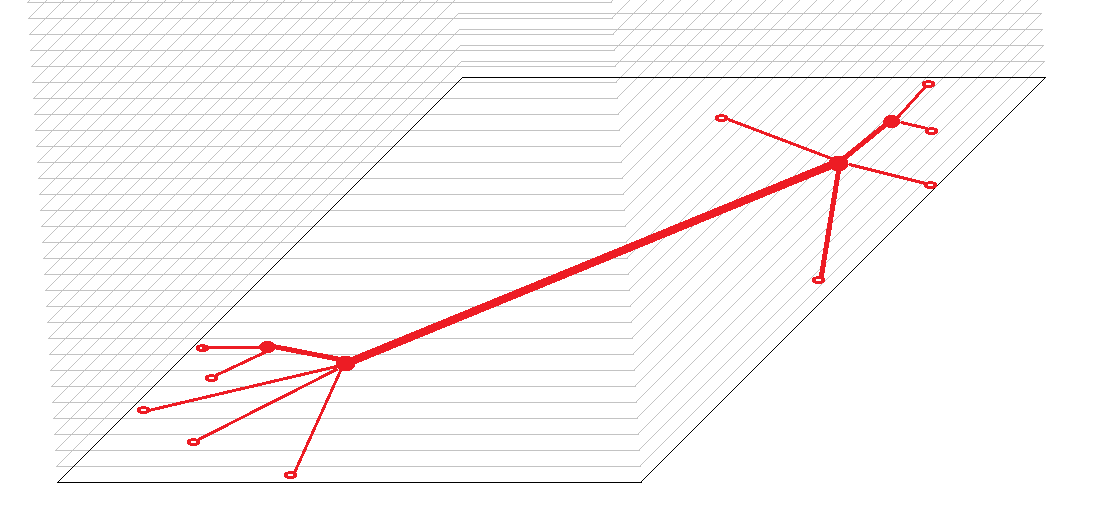
Рисунок 40 - Проекция схемы транспортировки на плоскость физического пространства

Решение этой задачи, традиционно формулируемое в разделе транспортных проблем, таким образом является не вполне адекватным по самой постановке, а имеющиеся в нашем распоряжении методы ее решения по большей части являются лишь приближенными и эвристическими.

Более того, до сих пор мы рассматривали всего лишь одну транспортную «транзакцию»: консолидацию грузов для формирования необходимой по экономическим соображениям грузовой партии магистрального единичного транспортного средства, перевозка этой партии и распределение отдельных грузов по пунктам назначения. Даже для одного такого маршрута, или «стринга», своя задача возникнет при движении транспортного средства на обратном плече маршрута. Следующий цикл, соответствующий новому круговому рейсу, так же будет связан с необходимостью решения схожих по структуре, но индивидуальных в отношении исходных данных задач. Совокупность различных стрингов одной компании формирует проблемное поле, многократно умножающее алгоритмическую сложность проблемы. Многообразие и многочисленность судоходных линий, присутствующих на рынке океанских, морских и каботажных перевозок, и вовсе лишает проблему их совокупной и частичной оптимизации имеющимися у современной математики средствами каких-либо перспектив.

В то же время, не знающие об этой методологической катастрофе грузоперевозчики продолжают успешно плавать по морю, грузовладельцы – пользоваться их услугами, инвесторы – вкладывать в них свой капитал в надежде его увеличить.