Импорт файлов из других приложений


1. Вызвать Outlook по алгоритмуВызов Outlook.

2. Выполнить команду Файл, Импорт и Экспорт...На экран выводится диалоговое окно Мастер импорта и экспорта(рис. 4.17).

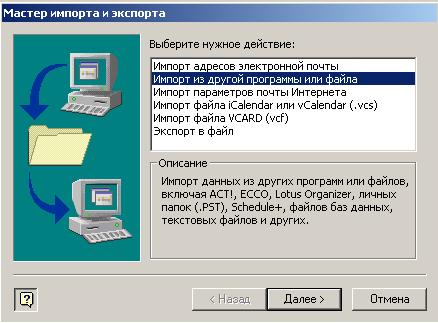
Рис. 4.17.Стартовое окно мастера импорта и экспорта Outlook

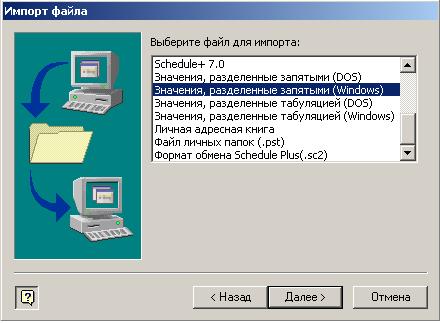
Рис. 4.18.Окно выбора типа файла для импорта

3. Выбрать необходимую процедуру. Выбираем строку, выделенную на рис. 4.17 ("Импорт из Schedule+, другой программы или файла").

4. Нажать кнопку Далее.На экране — окно, показанное на рис. 4.18.

5. Выбрать файл для импорта. Выбираем строку, выделенную на рис. 4.18.

6. Нажать кнопку Далее.На экране — окно Импорт файла(рис. 4.19).

7. Нажать кнопку Обзор...

8. Ввести имя файла того типа, который выбран в п. 5 (рис. 4.18).

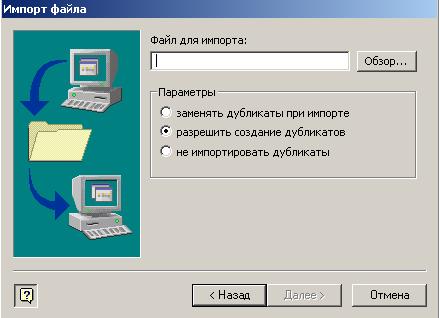
Рис. 4.19.Окно ввода имени файла мастера импорта и экспорта Outlook

9. Нажать кнопку ОК. На экране — импортируемый файл.

Выход в Internet

1. Вызвать Outlook по алгоритму Вызов Outlook.

2. Выполнить команду Справка.

3. Выбрать опцию Microsoft на Web (или Office в Интернете).На экране — меню (рис. 4.20).

4. Выбрать опцию Найти в Web...На экране — окно автоматически вызванной программы Internet Explorer для работ в Internet (рис. 4.21).

5. Ввести адрес Web.

Естественно, что компьютер при этом должен быть подключен к Internet.

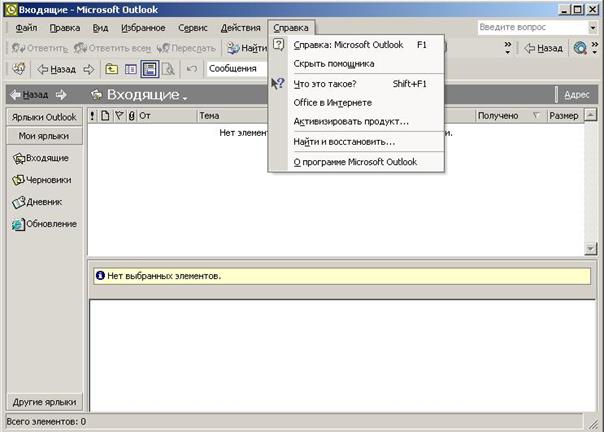
Рис. 4.20.Окно Outlook с меню входа в Internet

Рис. 4.21.Окно Internet Explorer


ГЛАВА 5. РЕШЕНИЕ ЗАДАЧ АНАЛИЗА И ОПТИМИЗАЦИИ С ИСПОЛЬЗОВАНИЕМ ТАБЛИЧНЫХ ПРОЦЕССОРОВ

Основой разработки и принятия решения является информация. От ее качества: достоверности, актуальности и точности зависит и результат в виде принимаемого решения. Необходимость одновременного учета множества факторов приводит необходимости принятия, наряду со структурируемыми, также полуструктурируемых и неструктурируемых решений. Существующие, развивающиеся и вновь создаваемые системы поддержки принятия решений (СППР)[1] имеют ориентацию не на процесс, а на набор возможностей интерактивно выбираемых менеджером. СППР предоставляет конечному пользователю не поддержку однозначно описанного процесса обработки данных, а набор возможностей, не зависящих от процесса. СППР являются основной категорией информационных систем управления, которые помогают менеджеру в процессе принятия неструктурированных и полуструктурированных решений. Специальное программное обеспечение СППР называется СППР – генераторами []. Электронные таблицы относятся к ограниченным СППР – генераторам. Отличительной и важной чертой СППР является использование базы моделей для поддержки решений. Часть моделей представляет и поддерживает рутинные вычисления, например, однофакторные и двухфакторные what-if модели (таблицы подстановки). Более сложные модели представляют связи между многими переменными. Например, к сложным моделям относят множественную регрессию, общую задачу линейного программирования, задачи математического программирования. Модели могут храниться в виде специальных программ, командных файлов, модулей и книг электронных таблиц.

5.1. Общие сведения о задачах оптимизации

5.1.1. Что такое оптимальное решение

Задачи оптимизации заключаются в поиске решения, обеспечивающего минимальное или максимальное значение некоторого критерия, называемого критерием оптимальности и представляющего функцию n действительных переменных F(x1, x2,..xn ). С математической точки зрения не играет существенной роли – будет ли мы рассматривать максимизацию или минимизацию, поскольку максимизация F эквивалентна минимизации -F. Значения переменных могут подчиняться ограничениям или изменяться без ограничений. Это зависит от конкретной задачи и ее постановки. В любой практической оптимизационной задаче существует много совпадающих этапов. Наиболее важным этапом является моделирование рассматриваемой физической ситуации с целью получения математической функции, которую необходимо, например, минимизировать, а также определения ограничений, если таковые существуют. Затем следует выбрать подходящую процедуру для осуществления минимизации. Эта процедура реализуется с помощью ПЭВМ, облегчая выполнение большого объема вычислений и представление результата. Наконец, математический результат должен быть интерпретирован в терминах физического содержания задачи.

Математическое моделирование позволяет достаточно быстро оценить результаты решения задачи и степень устойчивости полученного решения, в зависимости от изменения параметров модели (задачи). При разработке модели следует соблюдать следующие правила:

· Отделять главные свойства моделируемой задачи (объекта) от второстепенных;

· Учитывать главные свойства моделируемого объекта (элементы, характеристики, связи, параметры);

· Не включать в математическое описание второстепенных для данной задачи свойств

На этапе содержательной (физической) постановки задачи в этом процессе участвуют люди, работающие в данной предметной области, для которых все малейшие подробности описания процесса или объекта являются очень важными. При этом они исходят, часто, из ложной посылки, что чем больше информации включить в модель, чем она будет подробнее, тем лучше будет результат. Кроме того, известно, что на разных предприятиях используются разные методы оценки и анализа экономической ситуации, существуют сложившиеся воззрения о способах ее улучшения, поэтому всегда достаточно сложно сформулировать четко математическую постановку задачи в виде математической модели[2] ее решения.

На втором этапе выбирается и реализуется численный метод решения задачи в виде программы (программируется или используется стандартный пакет прикладных программ)

На третьем этапе интерпретируются и анализируются полученные результаты.

Существующие надстройки в электронной таблице MS Excel реализуют алгоритмы поиска оптимального решения на базе нелинейного метода оптимизации Л.Ласдона и А.Уорена, а также алгоритмы симплексного метода и «метода ветвей и границ» Д.Уотсона и Д.Филстра.

5.1.2. Классификация задач оптимизации

Важным этапом изучения явлений, предметов, процессов является их систематизация, которая обычно завершается классификацией по ряду признаков, а поскольку признаков может быть достаточно много, то и выполненные классификации могут различаться между собой. Любая классификация должна преследовать достижение поставленных целей. Выбор цели определяет набор тех признаков, по которым она будет проводиться.

Рассмотрим классификацию задач оптимизации по виду математических моделей, которые включают следующие элементы:

· исходные данные;

· искомые переменные;

· зависимости между переменными.

Исходными данными для математической модели являются: целевая функция F(Xj), левые части ограничений gi(Xj) и их правые части bi. Исходные данные могут быть детерминированными и случайными. Детерминированными называются такие исходные данные, когда при составлении модели их точные значения известны.

Искомые переменные могут быть непрерывными и дискретными. Непрерывными называются такие величины, которые в заданных граничных условиях могут принимать любые значения. Дискретными называются такие переменные, которые могут принимать только заданные значения. Целочисленными называются такие дискретные переменные, которые могут принимать только целые значения.

Зависимости между переменными (как целевые функции, так и ограничения) могут быть линейными и нелинейными. Напомним, что линейными называются такие зависимости, в которые переменные входят в первой степени и с ними выполняются только действия сложения или вычитания. Если же переменные входят не в первой степени или с ними выполняются другие действия, то зависимости являются нелинейными. При этом следует иметь в виду, что если в задаче хотя бы одна зависимость нелинейная, то и вся задача является нелинейной.

Сочетание различных элементов модели образует различные классы задач оптимизации, которые требуют разных методов решения. Основные классы задач оптимизации приведены в таблице 5.1.

Следует сразу уточнить, что в данном пособии мы рассмотрим решение подобных задач лишь на примере тех, которые относятся к классу линейного программирования. Решение задач такого рода зачастую необходимо при принятии оптимального решения в экономике.

Таблица 5.1.

Основные классы задач оптимизации.

Классы задач Характеристики элементов модели
Исходные данные Искомые переменные Зависимости
Линейного программирования Детерминированные Непрерывные Линейные
Целочисленного программирования Детерминированные Целочисленные Линейные
Нелинейного программирования Детерминированные Непрерывные, целочисленные Нелинейные
Стохастического программирования Случайные Непрерывные Линейные

5.2. Математическая формализация задачи

При построении математической модели решения задачи оптимизации искомые величины принимаются за неизвестные и составляется система неравенств, наиболее полно характеризующих решение поставленной задачи.

Оптимальное решение — это наилучшее. Но решения, наилучшего во всех смыслах, быть не может. Оно может быть наилучшим, т. е. оптимальным, только в одном, строго установленном смысле. И принимающий решение должен точно представлять, в чем заключается оптимальность решения, т. е. по какому критерию принимаемое решение должно быть наилучшим.

Определение 5.1.. Уравнение, описывающее критерий оптимизации принимаемого решения с математической точки зрения, называют целевой функцией.

В общем случае с помощью такой функции можно оценивать качества как желательные (например, прибыль, производительность, надежность), так и нежелательные (затраты, расход материала, простои оборудования). Тогда в первом случае стремятся к максимизации функции, а во втором — к ее минимизации. Кроме того, целевая функция может достигать определенного заданного значения.

Помимо целевой функции в любую математическую модель входят еще две составляющие:

1. Ограничения, которые устанавливают зависимости между переменными. Они могут быть как односторонними, например:

gi(xj) £ bi,

так и двусторонними

ai £ gi(xj) £ bi.

При решении задачи оптимизации с помощью Excel такое двустороннее ограничение записывается в виде двух односторонних ограничений

gi(xj) ³ аi.

gi(xj) £ bi.

Установленные ограничения должны отвечать требованию сопоставимости левой и правой части, которое заключается в следующем:

· однородность показателей, используемых в качестве левой и правой части неравенства;

· сопоставимость единиц измерения показателей, расположенных в левой и правой части неравенства;

· однородность временных интервалов, данные для которых используются в задаче.

2. Граничные условия показывают, в каких пределах могут быть значения искомых переменных в оптимальном решении.

Решение задачи, удовлетворяющее всем ограничениям и граничным условиям, называется допустимым. Если математическая модель задачи оптимизации составлена правильно, то задача будет иметь целый ряд допустимых решений. Поясним на примере следующей задачи, являющейся типичным примером задачи планирования производства:

Пример 5.1. Компания производит полки для ванных комнат двух типов - А и В. Агенты по продаже считают, что за неделю на рынке может быть реализовано до 550 полок. Для каждой полки типа А требуется 2 м2 материала, типа В - 3 м2 материала. Компания может получить до 1200 м2 материала в неделю. Для изготовления одной полки типа А требуется 12 мин. работы оборудования, а для изготовления одной полки типа В - 30 мин. Оборудование можно использовать 160 час. в неделю. Если прибыль от продажи полок типа А составляет 3 долл., а от полок типа В - 4 долл., то сколько полок надо выпускать в неделю, чтобы получить максимальную прибыль?

Составим математическую модель решения данной задачи.

1. Целевая функция.

Очевидно, что в качестве критерия оптимизации в данном случае выступает функция прибыли. Оптимальным будет считаться тот из вариантов решения, в котором значение прибыли будет максимальным. Учитывая, что «…прибыль от продажи полок типа А составляет 3 долл., а от полок типа В - 4 долл.…» целевая функция будет выглядеть следующим образом:

3x1 + 4x2 " max,

где x1 – объем производства полок типа A, x2 – объем производства полок типа B.

2.Ограничения:

а) ограничение на объем производства: «…Агенты по продаже считают, что за неделю на рынке может быть реализовано до 550 полок…» Очевидно, что совокупный объем производства полок не должен превышать 550 единиц, или, в математическом виде:

x1 + x2 £ 550;

б) ограничения на используемые ресурсы: В данной задаче используются ресурсы двух видов: оборудование и материалы:

ограничение на использование оборудования: «…Для изготовления одной полки типа А требуется 12 мин. работы оборудования, а для изготовления одной полки типа В - 30 мин. Оборудование можно использовать 160 часов в неделю…» На основе этой информации можно сделать вывод, что общее время использования оборудования в рамках данного проекта не должно превышать 160 часов в неделю. Переведя время, необходимое для изготовления одной полки в часы (с целью сопоставимости единиц измерения правой и левой части неравенства) получим:

0,2x1 + 0,5x2 £ 160;

ограничение на использование материалов: «…Для каждой полки типа А требуется 2 м2 материала, для полки типа В - 3 м2 материала. Компания может получить до 1200 м2 материала в неделю…» На основе этой информации можно сделать вывод, что общее количество материала, затрачиваемого для реализации данного проекта не должно превышать 1200 м2:

2x1 + 3x2 £ 1200.

3. Граничные условия.

В качестве граничных условий в данном примере могут быть использованы следующие утверждения, вытекающие из сути поставленной задачи:

a) Объем производства полок типа А и полок типа В – неотрицательное значение.

b) Объем производства полок типа А и полок типа В – целое число.

x1, x2 ³ 0

x1, x2 – целое

5.3. Решение задачи в среде MS EXCEL (на примере задачи планирования производства)

5.3.1. Ввод условий задачи

Ввод условий задачи состоит из следующих основных шагов:

1. Создание формы для ввода данных, необходимых для последующего решения.

2. Ввод исходных данных и зависимостей из математической модели.

3. Указание целевой ячейки (ячейки, в которую введена целевая функция), ввод ограничений и граничных условий в диалоговом окне Поиск решения.

Создание формы для ввода данных.

Такая форма должна содержать возможность ввода всех данных, необходимых для решения поставленной задачи:

· искомых переменных;

· целевой функции;

· правой и левой части неравенств, описывающих ограничения, налагаемые на возможные варианты решения поставленной задачи.

Примерная форма для ввода данных, необходимых для решения «задачи о полках» текст которой приведен выше, представлена на рис. 5.1.

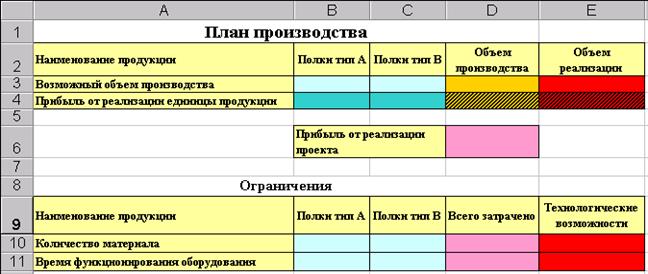
Рис. 5.1. Примерная форма для ввода условий задачи

Ввод исходных данных и зависимостей из математической модели.

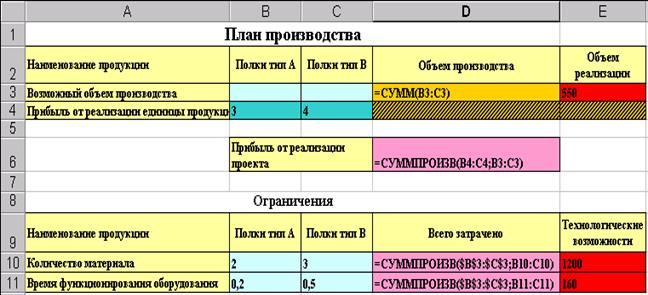
Рис. 5.2. Условия решения задачи

Отметим, что целевая функция и левые части неравенств, определяющих возможные варианты решения поставленной задачи, вводятся формулой, в которой роль искомых переменных играют адреса ячеек, зарезервированных для вывода их значений после решения задачи, а роль коэффициентов – адреса ячеек, содержащих соответственные коэффициенты.[3]

Назначение целевой функции, ввод ограничений и граничных условий.

Данная стадия ввода условия задачи осуществляется в диалоговом окне Поиск решения (см. рис. 5.3.) для открытия которого необходимо в меню Сервис выбрать команду Поиск решения.[4]

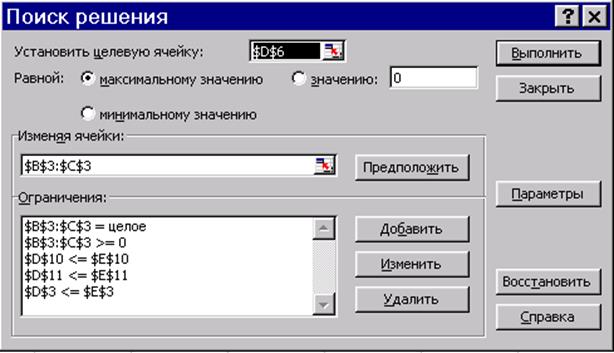
Рис. 5.3. Диалоговое окно Поиск решения

В этом диалоговом окне пользователь должен:

1. Назначить целевую ячейку. Для этого в поле «Установить целевую ячейку:» вводится адрес ячейки, содержащей целевую функцию. Затем устанавливается направление последней – значение, к которому она должна стремиться исходя из условий задачи (минимальное, максимальное, конкретное, задаваемое пользователем).

2. В поле «Изменяя ячейки:» ввести адреса ячеек, зарезервированных для искомых переменных.

3. Ввести ограничения и граничные условия. Для этого в диалоговом окне Поиск решения (см. рис. 5.3.) нажать на кнопку Добавить. В открывшемся диалоговом окне Добавление ограничений (см. рис. 5.4.):

· в поле «Ссылка на ячейку:» ввести адрес ячейки листа, содержащей формулу для расчета показателя, используемого в качестве левой части неравенства,

· из списка знаков неравенств выбрать необходимый знак,

· в поле «Ограничение:» указать адрес ячейки, содержащей показатель, используемый в качестве правой части неравенства.[5]

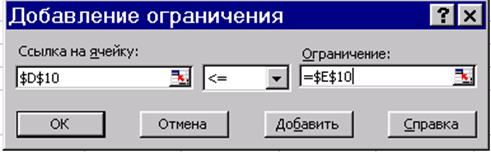
Рис. 5.4. Диалоговое окно Добавление ограничений

Добавление каждого последующего ограничения осуществляется с помощью кнопки Добавить. После окончания ввода ограничений необходимо нажать Ok

5.3.2. Решение задачи

Установка параметров решения задачи.

С помощью команд, находящихся в диалоговом окне Параметры поиска решения[6](рис. 5.5), можно вводить условия для решения задач оптимизации всех классов.

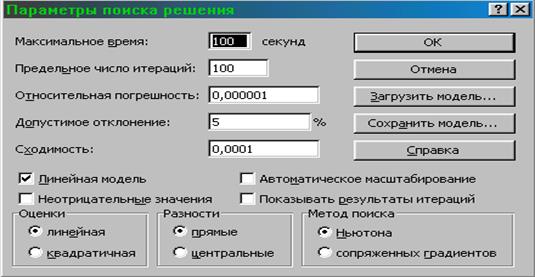
Рис. 5.5. Диалоговое окно Параметры поиска решения

Познакомимся с основными элементами данного окна, которые могут потребоваться при решении задач линейного программирования.

Поле «Максимальное время»

Служит для назначения времени в секундах, выделяемого на поиск решения задачи. В поле можно ввести время, не превышающее 32767 с (более 9 часов!). Значение 100, используемое по умолчанию, подходит для решения большинства задач.

Поле «Предельное число итераций»

Служит для назначения числа итераций. Используемое по умолчанию значение 100 подходит для решения большинства задач.

Поля «Относительная погрешность» и «Допустимое отклонение»

Служат для задания точности, с которой отыскивается решение. Рекомендуется после нахождения решения со значениями данных параметров, заданных по умолчанию, повторить вычисления с большей точностью и меньшим допустимым отклонением и сравнить с первоначальными результатами. Использование подобной проверки особенно рекомендуется при решении задач с целочисленными ограничениями на переменные.

Флажок «Линейная модель»

Служит для поиска решения линейной задачи оптимизации или линейной апроксимации нелинейной задачи. Для линейной задачи этот флажок должен быть установлен, т.к. в противном случае возможно получение неверного результата.

Получение результата

После нажатия на кнопку Выполнить диалогового окна Поиск решения на экране появляется диалоговое окно Результаты поиска решения (рис. 5.6.). Решение найдено, и его результаты приведены в таблице (рис. 5.7).

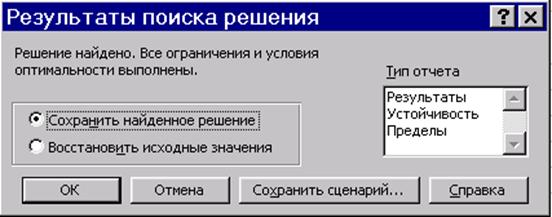
Рис. 5.6. Диалоговое окно Результаты поиска решения

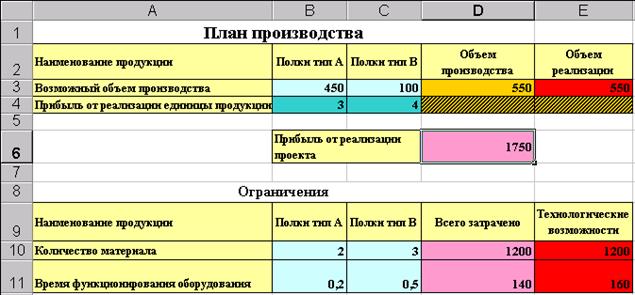
Рис. 5.7. Результаты решения задачи

Из рисунка видно, что оптимальное решение поставленной задачи предполагает производство:

· полок типа А в количестве 450 штук (В3);

· полок типа В – в количестве 100 штук (С3).

При этом максимальная прибыль будет составлять 1720 единиц, а ресурсы используются следующим образом:

· потребление материала – 1200 единиц (D10);

· использование оборудования – 140 часов (D11).

5.4. Анализ полученного решения

MS Excel дает пользователю возможность получить набор отчетов, содержащих определенную информацию о решении задачи. На основе сведений из этих отчетов можно спрогнозировать изменение результата при модификации параметров модели.

5.4.1. Назначение имен ячейкам

При анализе удобно присвоить запоминающиеся имена ячейкам исходных данных. Дело в том, что при создании отчетов мастер отчетов должен сопоставить каждой заносимой в отчет ячейке какой-то идентификатор. Если имена ячеек не заданы, то по умолчанию для этого используются ссылки (например H9). Отчет с такими подписями к ячейкам не слишком информативен. Чтобы понять значение каждой занесенной в него цифры, нужно будет составить таблицу соответствия ссылок и данных.

Чтобы присвоить имя ячейке (диапазону ячеек) следует:

1. Выделить ячейку или диапазон, который вы хотите поименовать.

2. Выполнить командуВставка Þ Имя Þ Присвоить.

3. В открывшемся диалоговом окне Присвоение имени (см. рис. 5.8.) в поле Имя ввести желаемое название[7] и нажать OK.

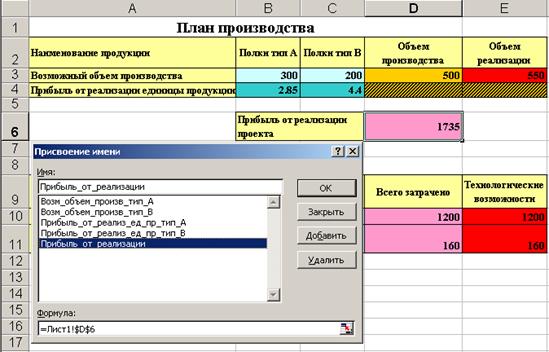
Рис. 5.8. Диалоговое окно Присвоение имени

5.4.2. Анализ оптимального решения

Анализ оптимального решения начинается после успешного решения задачи, когда на экране появляется диалоговое окно Результат поиска решения если решение найдено (рис. 5.5). С помощью этого диалогового окна можно вызвать отчеты трех типов:

· результаты;

· устойчивость;

· пределы.

Отчет по результатам.

Отчет состоит из целевой ячейки и списка влияющих ячеек модели, их исходных и конечных значений, а также формул ограничений и дополнительных сведений о наложенных ограничениях (см. рис. 5.9).

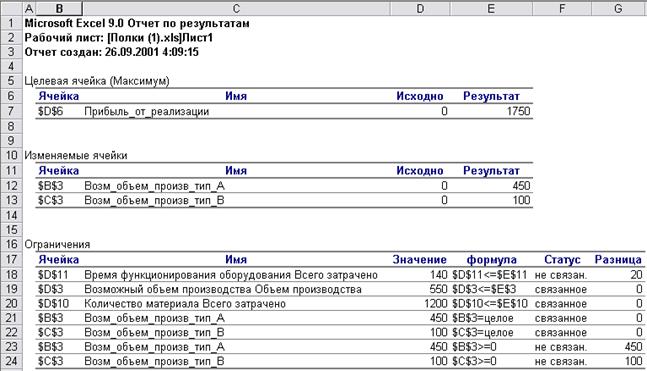
Рис. 5.9. Отчет по результатам

Наибольший интерес в данном отчете вызывает блок «Ограничения». Остановимся на нем подробнее:

· Поле Ячейка содержит адреса ячеек, указанных в качестве левой части ограничений и граничных условий (см. рис. 5.3).

· Поле Имя содержит присвоенное пользователем имя (см. п.5.4.1) для указанных ячеек.

· Поле Значение содержит значение, полученное в указанных ячейках в результате решения задачи.

· Поле Формула содержит ограничения и граничные условия, введенные пользователем (см. рис. 5.3).

· Поле Статуспоказывает наличие разницы между значениями, полученными в результате решения задачи в указанных ячейках и значениями, указанными пользователем как критические (правые части ограничений и граничных условий). Если в данном поле стоит «связанное» разница равна нулю. В противном случае – разница отлична от нуля.

· Поле Разница содержит цифровое значение выявленной разницы.

Отчет по устойчивости.

Отчет содержит сведения о чувствительности решения к малым изменениям в формуле модели или формулах ограничений. Такой отчет не создается для моделей с целочисленными ограничениями, налагаемыми на переменные.

Отчет по пределам.

Отчет состоит из целевой ячейки и списка влияющих ячеек модели, их значений, а также нижних и верхних границ. Такой отчет не создается для моделей с целочисленными ограничениями, налагаемыми на переменные. Нижним пределом является наименьшее значение, которое может содержать влияющая ячейка, в то время как значения влияющих ячеек фиксированы и удовлетворяют наложенным ограничениям. Соответственно верхним пределом является максимальное значение.

5.4.3. Параметрический анализ

Часто, при решении разного рода задач, перед нами встает необходимость смоделировать влияние изменения какого либо параметра на решение задачи. Ощутимую пользу в анализе такого рода могут оказать сценарии Excel.

Сценарий Excel представляет собой зафиксированный в памяти компьютера набор значений ячеек рабочего листа. Таким образом, создав сценарий, пользователь получает возможность узнать, что произойдет с результатом, если поменять исходные значения в некоторых ячейках листа. Данная информация будет содержаться в отчете по сценарию.

Рассмотрим данный вид анализа на примере нашей задачи. Предположим, что перед вами поставлена задача рассмотреть два плана ценообразования:

a. обеспечивающий прибыль 3 единицы от реализации одной полки типа А и 4 единицы – типа В;

b. обеспечивающий прибыль 2,85ед. от реализации одной полки типа А и 4,4 единицы – типа В

и выбрать тот, суммарная прибыль при котором наибольшая.

Создание сценария.

Чтобы решить поставленную задачу мы должны каждый вариант решения записать как сценарий. Для этого на завершающей стадии решения задачи в диалоговом окне Результаты поиска решения (рис. 5.5) необходимо нажать на кнопку Сохранить сценарий…

Появляется диалоговое окно Сохранение сценария (рис. 5.10) в котором достаточно ввести название текущего сценария и нажать OK после чего завершить решение задачи в обычном порядке.

Рис. 5.10. Диалоговое окно Сохранение сценария

Диспетчер сценариев.

Вся дальнейшая работа со сценариями осуществляется в диалоговом окне Диспетчер сценариев (рис. 5.11), которое выводится если в меню Сервис выбрать команду Сценарии…. С его помощью можно:

· Вывести записанные в сценарий значения на лист книги MS Excel;

· Добавить новый сценарий[8];

· Удалить нежелательный сценарий;

· Изменить параметры сценария;

· Объединить сценарии схожей структуры расположенные в разных рабочих книгах;

· Вывести Отчет содержащий информацию по нескольким сценариям.

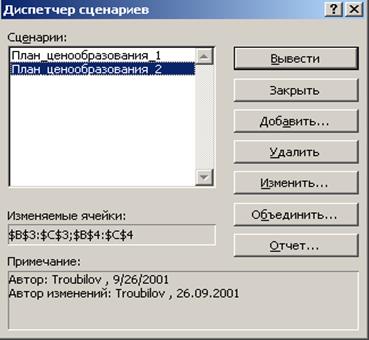
Рис. 5.11. Диалоговое окно Диспетчер сценариев

Изменение сценария.

По умолчанию в качестве ячеек, значения которых хранятся в сценарии, при решении задач оптимизации указаны ячейки, содержащие значения искомых переменных (т.е. ячейки, значения которых будут меняться автоматически в каждом последующем сценарии). Чтобы дополнить этот перечень ячейками, значения в которых будут меняться пользователем, необходимо Изменить сценарий. Для этого в диалоговом окне Диспетчер сценариев выделяется название изменяемого сценария после чего нажимается кнопка Изменить….

В открывшемся диалоговом окне Изменение сценария (рис. 5.12) в поле Изменяемые ячейки сформировать полный перечень ячеек, значения которых должны храниться в сценарии[9] и нажать OK. Открывается диалоговое окно Значения ячеек сценария (рис. 5.13) в котором, если нужно, можно поменять конкретные значения, которые будут храниться в соответствующем сценарии.

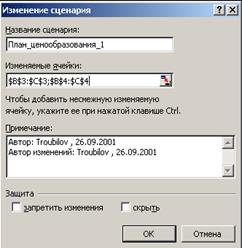
Рис. 5.12. Диалоговое окно Изменение сценария

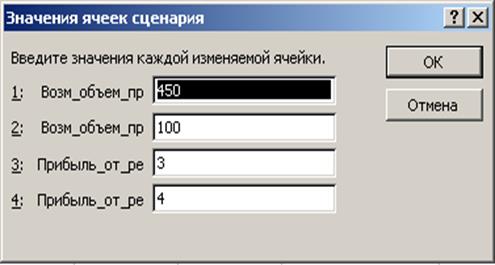
Рис. 5.13. Диалоговое окно Значения ячеек сценария

Результаты работы.

Для предоставления результатов MS Excel предлагает два вида отчетов:

· итоговый отчет, в котором подробно расписывается структура каждого сценария;

· отчет в виде сводной таблицы.

При решении задач оптимизации чаще всего используется первый (рис. 5.14), который предпочтительнее когда имеется простой набор сценариев, в каждом из которых несколько изменяемых переменных. Второй же хорошо подходит для создания сводок о работе при использовании нескольких наборов, так как он позволяет рассмотреть все возможные комбинации сценариев.

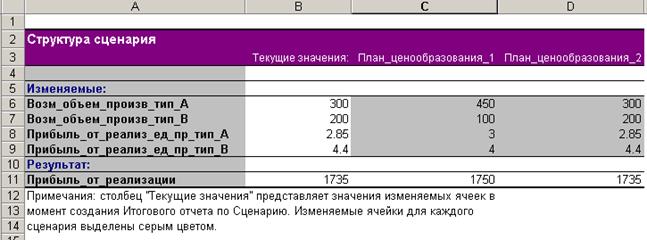
Рис. 5.14. Отчет типа Структура сценария

Даже беглого взгляда на этот отчет достаточно, чтобы определить, что первый план ценообразования предпочтительнее.

 

5.5. Примеры решения задач оптимизации

В этом разделе рассмотрено решение типовых экономических задач в электронных таблицах MS Excel. Разумеется, что возможности электронных таблиц не ограничиваются решением задач планирования производства или штатного расписания, транспортной задачи и задачи о назначениях ресурсов. Любая задача, допускающая построение математической модели (см. предыдущий раздел), может быть проанализирована средствами MS Excel. Заинтересованный читатель найдет дополнительные сведения о решении задач оптимизации в Приложении.

5.5.1. Транспортная задача

Предположим, что ваша фирма занимается производством и продажей продукции. Фирма владеет несколькими заводами, где эта продукция производится, и имеет ряд магазинов. Каждый завод обладает определенными производственными мощностями, а каждый магазин – объемом продаж товара. Для обеспечения высокой эффективности работы фирмы необходимо спланировать перевозки товаров так, чтобы транспортные затраты были как можно меньше. При этом требуется обеспечить вывоз всей продукции с каждого завода и полностью удовлетворить запросы каждого магазина. Для простоты будем полагать, что общий объем производства равен общему объему спроса (сбалансированная задача).

Для решения задачи построим ее математическую модель. Обозначим количество заводов N, а количество магазинов M. Для нумерации заводов и магазинов введем индексы i и j. Индекс i пробегает целочисленные значения от 1 до N и указывает номер завода, индекс j принимает значения от 1 до M и соответствует номеру магазина. Объем производства i-го завода обозначим ai, объем спроса j-го магазина - bj. Условие баланса спроса и предложения имеет вид

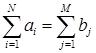. (5.5.1)

Неизвестными величинами в данной задаче являются объемы перевозок, которые мы обозначим xij. Величина xij – это объем перевозок с i-го завода в j-й магазин. Затраты на перевозку единицы продукции из пункта i в пункт j по аналогии обозначим cij. Очевидно, что величины xij и cij в нашей задаче могут принимать лишь неотрицательные значения

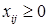, (5.5.2.)

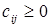. (5.5.3)

Стоимость одной перевозки составит xijcij, а общие транспортные расходы Z будут складываться из затрат по каждому маршруту:

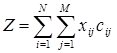. (5.5.4)

По условию задачи требуется минимизировать совокупные затраты на перевозки. В нашей модели оптимальному графику перевозок соответствует минимальное значение функции Z. Если не накладывать на величины xij и cij дополнительных условий и попытаться минимизировать целевую функцию (3.5.4), то в результате мы получим Z = 0 и xij = 0. Такой результат, очевидно, не может быть удовлетворительным ответом. Для правильного решения поставленной задачи необходимо ввести ограничения на объемы вывозимой и ввозимой продукции. Объем вывозимой с i-го завода продукции должен быть равен объему производства ai, объем ввозимой продукции должен соответствовать объему спроса bj:

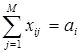, (5.5.5)

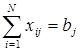. (5.5.6)

Выражения (5.5.1)-(5.5.6) составляют математическую модель сбалансированной транспортной задачи. Если спрос и предложение не сбалансированы, то в модель нужно ввести фиктивные пункты производства или пункты потребления. В случае дефицита вводится фиктивный завод, стоимость и объем перевозок с которого равны штрафу за недопоставку и объему недопоставки соответственно. В случае перепроизводства продукции вводится фиктивный магазин, стоимость и объем перевозок в который полагается равной стоимости складирования и объему излишней продукции соответственно.

Рассмотрим решение сбалансированной транспортной задачи средствами MS Excel. Пусть имеется 3 завода (N=3) и 4 магазина (M=4). Введем в рабочий лист данные об объемах производства и спроса как показано на
рис. 3.15. Для проверки баланса (выражение (3.5.1)) просуммируем значения в диапазонах B4:B6 и G4:G7, затем сравним вычисленные суммы в ячейке C10 с помощью формулы

«=ЕСЛИ(B7=G8;"Задача сбалансирована";"Нарушен баланс!")».

Далее в диапазон B14:E16 вводим данные о себестоимости перевозок между заводами и магазинами.

Для распределения объемов перевозок между экономическими объектами создадим таблицу «Объемы перевозок» (рис. 5.16). Для проверки условий (5.5.5) и (5.5.6) в ячейках B23:E23 и F20:F22 вычислим суммы строк и столбцов таблицы «Объемы перевозок». Суммы по столбцам соответствуют объемам ввозимой продукции, а по строкам – объемам вывозимой продукции. Значения объемов перевозок заранее неизвестны, для определенности в качестве начального приближения вводим в ячейки B20:E22 нулевые значения. Для вычисления целевой функции (5.5.4) введем в ячейку E25 формулу

«=СУММПРОИЗВ(B14:E16;B20:E22)».

Теперь рабочий лист содержит всю необходимую информацию для «Поиска решения». Выполним команду «Сервис|Поиск решения» и заполним поля открывшегося диалогового окна (рис. 5.17). Условия (5.5.2), (5.5.5) и (5.5.6) вводим в диалог «Поиск решения» в виде ограничений. Для корректного решения линейной задачи установим флажок «Линейная модель» (кнопка «Параметры»). После нажатия кнопки «Выполнить» «Поиск решения» находит оптимальный план перевозок грузов, показанный на рисунке 5.16.

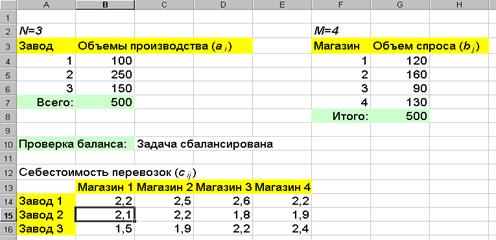
Рис. 5.15. Исходные данные транспортной задачи

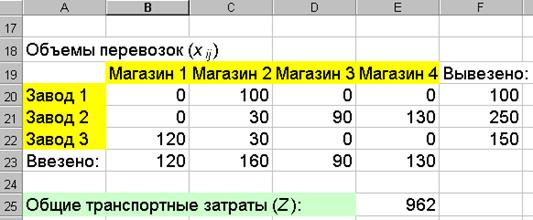
Рис. 5.16. Оптимальное решение транспортной задачи

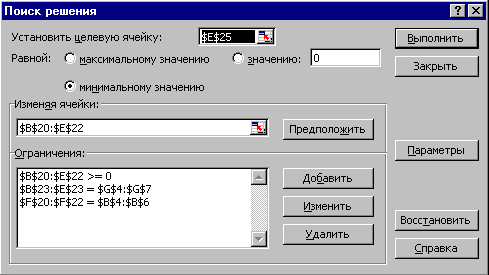
Рис. 5.17. Диалоговое окно «Поиск решения» для транспортной задачи

Рис. 5.13. Диалоговое окно Значения ячеек сценария

Результаты работы.

Для предоставления результатов MS Excel предлагает два вида отчетов:

·итоговый отчет, в котором подробно расписывается структура каждого сценария;

·отчет в виде сводной таблицы.

При решении задач оптимизации чаще всего используется первый (рис. 5.14), который предпочтительнее когда имеется простой набор сценариев, в каждом из которых несколько изменяемых переменных. Второй же хорошо подходит для создания сводок о работе при использовании нескольких наборов, так как он позволяет рассмотреть все возможные комбинации сценариев.

Рис. 5.14. Отчет типа Структура сценария

Даже беглого взгляда на этот отчет достаточно, чтобы определить, что первый план ценообразования предпочтительнее.

5.5.2. Задача о назначениях

В распоряжении бригадира имеются N рабочих, каждого из которых нужно назначить на выполнение одной из N работ. Рабочие имеют разную квалификацию, поэтому стоимости cij выполнения i-м рабочим j-й работы различны. Бригадир должен распределить рабочих так, чтобы общая стоимость работ Z была минимальной. При этом каждый рабочий должен быть загружен только на одной работе и все работы - выполнены. Заметим, что в данной задаче число рабочих и работ совпадает, т.е. задача является сбалансированной. В случае несбалансированной задачи ее необходимо предварительно сбалансировать путем введения фиктивных рабочих или видов работ с достаточно высокими штрафными стоимостями работ.

Построим математическую модель данной задач


Дата добавления: 2021-01-26; просмотров: 355;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.074 сек.