Краткие сведения о ползучести и релаксации
Ползучестью называется способность материала деформироваться во времени при действии постоянных нагрузок.
Явление ползучести присуще таким материалам, как бетон, кирпич, полимеры, древесина. Металлы также обнаруживают это свойство деформирования, которое становится особенно заметным при высокой температуре, а в цветных металлах (свинец, медь и др.) даже при комнатной температуре.
Фактор ползучести имеет существенное значение для работы конструкций. Достаточно отметить, что напряжения в арматуре железобетонных конструкций могут в процессе ползучести увеличится в 2-2,5 раза, а перемещения – в 3-4 раза. В машиностроении известны случаи, когда стальные котельные трубы разрушались под действием внутреннего давления вследствие ползучести материала. На рис.12.4 показано разрушение трубы из-за ползучести материала (пунктиром на рисунке нанесены первоначальные и изменяющиеся размеры поперечного сечения трубы).
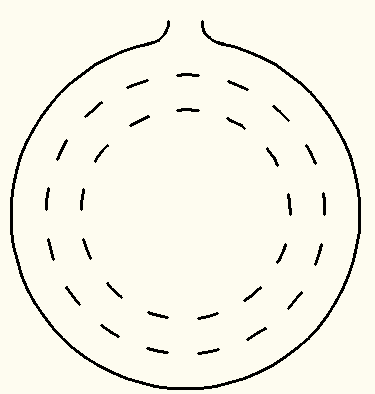
Рисунок 12.4 – Разрушение трубы из-за ползучести материала
Деформация ползучести 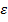 может рассматриватся как очень медленная текучесть маталла. Схематически диаграмму ползучести можно изобразить упрощенной зависимостью
может рассматриватся как очень медленная текучесть маталла. Схематически диаграмму ползучести можно изобразить упрощенной зависимостью 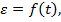 где
где 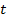 – время деформирования материала при ползучести (рис. 12.5).
– время деформирования материала при ползучести (рис. 12.5).
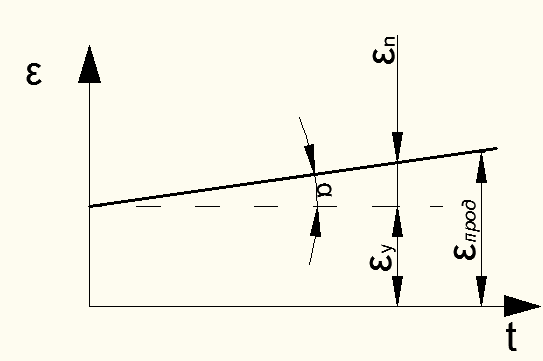
Рисунок 12.5 – Диаграмма ползучести
Пренебрегая временем на осуществление упругой деформации 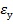 , можно представить возрастание деформаций в виде
, можно представить возрастание деформаций в виде 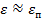 , где
, где 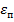 - деформация ползкчести в условиях ползучести материала:
- деформация ползкчести в условиях ползучести материала:
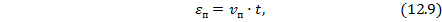
где 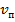 – постоянная скорость ползучести, равная
– постоянная скорость ползучести, равная
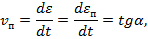
α – угол наклона условной линии ползучести (см.рис.12.5).
Условие прочности при ползучести имеет вид:
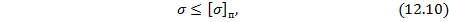
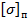 – передел ползучести, рассматриваемый как наибольшее напряжение, при котором получаем малую скорость ползучести и пластическую деформацию определенной величины
– передел ползучести, рассматриваемый как наибольшее напряжение, при котором получаем малую скорость ползучести и пластическую деформацию определенной величины 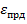 (см. рис. 12.5) за весь срок службы материала при заданной температуре.
(см. рис. 12.5) за весь срок службы материала при заданной температуре.
В задачах расчета деталей машин на ползучесть, кроме проверки условия прочности (12.10), обычно определяется и срок службы детали tg, когда скорость ползучести 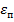 не превосходит попускаемую скорость
не превосходит попускаемую скорость 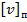 при заданном предельном сроке службы детали
при заданном предельном сроке службы детали 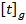 .
.
Вместе с ползучестью деталям свойственно и такое явление, как релаксация. Релаксацией называется уменьшение напряжений в детали в результате постоянного нарастания пластической деформации за счет упругой.
Благодаря релаксации плотность соединения деталей, скрепленных за счет упругого натяга, может быть настолько ослаблена, что вызовет нарушение нормальной работы конструкции. Так, например, ослабление плотности болтового соединения фланцев газопровода или цилиндров высокого давления паровой турбины может привести к утечке газа или пара, если не проводить периодические ремонтные работ фланцевого соединения. Таким образом, с явлением релаксации необходимо считаться в процессе эксплуатации машин и механизмов.
При релаксации имеет место процесс постепенного снижения напряжений в нагруженной детали, полная деформация которой не может изменятся во времени и равна полученной при нагружении упругой деформации. При этом снижение напряжений происходит вследствие постепенного уменьшения упругой деформации и приращения на ту же величину пластической деформации на основании зависимостей:
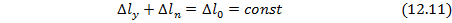
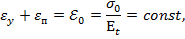
где 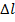 – изменение длины детали соответственно в упругой и пластических областях при деформации
– изменение длины детали соответственно в упругой и пластических областях при деформации 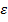 ;
; 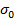 – первоначальное напряжение в детали;
– первоначальное напряжение в детали; 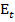 – модуль упругости материала при заданной температуре.
– модуль упругости материала при заданной температуре.
Дифференциальную вторую зависимость (12.11) по времени t и заменяя 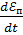 на
на 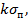 получаем дифференциальное уровнение, решение которого дает функциональную зависимость напряжения в детали от времени при релаксации
получаем дифференциальное уровнение, решение которого дает функциональную зависимость напряжения в детали от времени при релаксации 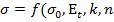 ), где
), где 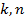 – опытные коэффициенты, зависящие от свойств материала и температуры эксплуатации.
– опытные коэффициенты, зависящие от свойств материала и температуры эксплуатации.
Основные понятия о расчете элементов конструкций в области пластических деформаций
12.4.1. Расчет элементов конструкции по несущей способности
До сих пор в проведенных расчетах прочности элементов конструкций в упругой области при статическом нагружении рассматривался метод допускаемы напряжений. По этому методу условия прочности элемента конструкции считались нарушенными, если хотя бы в одной точке этого элемента напряжение достигало опасной величины – допускаемого напряжения (такой подход именуется еще расчетом по опасной точке).
Для расчета конструкций из пластичных материалов типа стали при статическом наружении возможен и другой подход к оценке их прочности – расчет по методу продольного состояния, или несущей способности. При этом считается, что достижение предела текучести в одной точке (точках) не приводит к выходу из строя всей конструкции и ее состояние не считается предельным. Несущая способность конструкции будет исчерпана, когда она обратится в геометрически изменяемую систему при неограниченном деформировании при постоянной нагрузке. Такая нагрузка (сила или момент) считается предельной нагрузкой, а состояние конструкции именуется предельным и соответствует исчерпанию ее несущей способности.
Расчет прочности элементов конструкции или ее в целом при таком условии называется расчетом по предельному состоянию, или расчетом по несущей способности. Такой подход является более простым в расчете по учету пластических деформаций, которые могут возникнуть в конструкции и их элементах.
Условие прочности по предельному состоянию (нагрузке) записывается в виде:
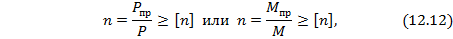
где 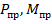 – предельное значение нагрузки (силы или момента), при котором несущая способность конструкции будет исчерпана;
– предельное значение нагрузки (силы или момента), при котором несущая способность конструкции будет исчерпана;
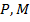 – действующая нагрузка на кострукцию;
– действующая нагрузка на кострукцию;
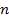 – действительный коэффициент запаса прочности;
– действительный коэффициент запаса прочности;
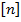 – требуемый (заданный) коэффициент запаса прочности.
– требуемый (заданный) коэффициент запаса прочности.
Часто расчеты по несущей способности базируются на том, что материал конструкции является идеально упругопластичным. Схематизированная диаграмма деформирования такого материала определяется упрощенной диаграммой растяжения (рис.12.6). Обычно предполагается, что диаграмма сжатия такая же (в пределах относительно малых пластических деформаций), как и при растяжении.
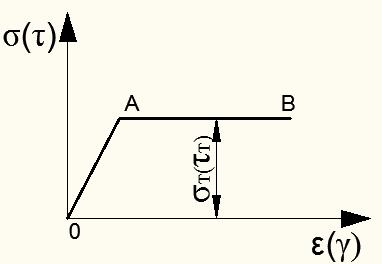
Рисунок 12.6 – Схематизированная диаграмма растяжения материала
Диаграмма состоит из двух прямолинейных участков ОА и АВ (см. рис. 12.6).
Участок ОА соответствует упругой деформации материала, где соблюдается закон Гука. Предполагается, что крайнее значение участка – предел пропорциональности материала – равны пределам текучести, т.е. 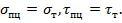
Второй участок диаграммы АВ соответствует состоянию текучести материала, причем считается, что площадка текучести имеет неограниченную протяженность.
Применение такой схематизированной диаграммы «напряжения σ(τ) – деформации 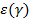 ′′ (она называется диаграммой Прандля) существенно упрощает расчеты по несущей способности.
′′ (она называется диаграммой Прандля) существенно упрощает расчеты по несущей способности.
В статически определимых системах, элементы которых работают на растяжение и сжатие, результаты расчета по несущей способности совпадают с результаты расчета по опасной точке. Действительно, нагрузка текучести возникает во всех точках наиболее напряженного элемента конструкции и переход в состояние текучести всех элементов превращает систему в геометрически изменяемую.
В статически неопределимой системе, элементы которой в упругой стадии работы нагружены различно, возникновение текучести в каком-либо элементе не приводит к исчерпанию несущей способности всей системы, так как остальные элементы системы находятся в упругой стадии и еще не способны оказывать сопротивление возрастающей нагрузке. В этих случаях предельная нагрузка 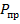 будет больше
будет больше 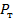 , при котрой текучесть возникает лищь в одном элементе. Отсюда следует, что допускаемая нагрузка для статически неопределимой системы, рассчитанной по несущей способности, будет больше, чем в случае расчета этой системы по опасной точке при одинаковых коэффициентах запаса прочности.
, при котрой текучесть возникает лищь в одном элементе. Отсюда следует, что допускаемая нагрузка для статически неопределимой системы, рассчитанной по несущей способности, будет больше, чем в случае расчета этой системы по опасной точке при одинаковых коэффициентах запаса прочности.
В общем случае, коэффициенты запаса при расчете по несущей способности будут выше, чем при по расчете по опасной точке.
Когда в упругой стадии работы системы напряжения в поперечных сечениях ее элементов распределены неравномерно (например, при кручении или изгибе), расчет по несущей способности дает результат, отличный от расчета по опасной точке, даже если система статические определима.
12.4.2. Расчет несущей способности бруса на растяжение (сжатие)
Пример 12.1. Определить по расчету несущей способности допускаемую величину силы Р для статически неопределимого бруса (рис. 12.7). Материал бруса Ст.3 с пределом текучести 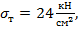 требуемый коэффициент запаса прочности
требуемый коэффициент запаса прочности 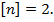
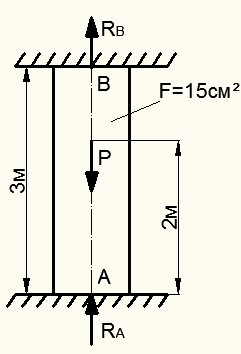
Рисунок 12.7 – К расчету несущей способности бруса
Решение
Обозначив реакции в защемлении концов бруса 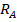 и
и 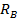 , составим уравнение равновесия:
, составим уравнение равновесия:
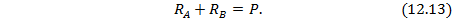
Из условия нагружения бруса силой Р (см. рис. 12.7) видно, что верхняя часть бруса от места приложения силы испытывает растяжение с растягивающим усилием 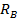 , а нижняя часть – сжатие при сжимающем усилии
, а нижняя часть – сжатие при сжимающем усилии 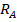 .
.
В предельном состоянии конструкции напряжения в обеих частях бруса достигают предела текучести 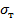 и отсюда реакции равны:
и отсюда реакции равны:
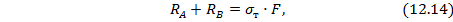
где F – площадь поперечного сечения бруса.
Подставляя значения реакций (12.4) в уравнение (12.13) и учитывая, что в предельном состоянии усилие Р достигает своего предельного значения, имеем:
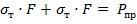
или
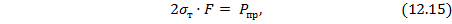
откуда
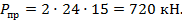
Учитывая коэффициент запаса прочности 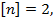 допускаемая нагрузка равна:
допускаемая нагрузка равна:
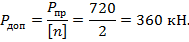
12.4.3. Расчет несущей способности балок при поперечном изгибе
В расчет на изгиб балки из пластичного материала по методу допускаемых напряжений опасным считается то состояние балки, при котором в опасном сечении по ее длине в крайних его точках А, В максимальные напряжения достигают предела текучести материала (рис. 12.8, б).
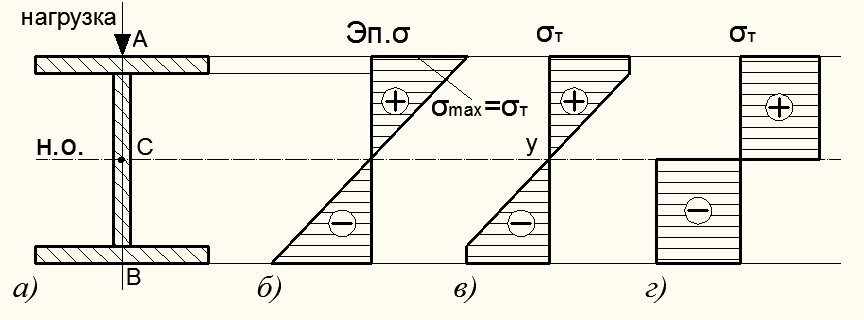
Рисунок 12.8 – Эпюры нормальных напряжений балки при изгибе
По мере возрастания нагрузки, а значит величины изгибающего момента в опасном сечении балки, текучесть будет охватывать все большую площадь сечения: одна его часть будет работать упруго, а другая часть – охвачена пластическими деформациями при напряжениях 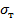 (рис. 12.8, в). Наконец, текучестью будет охвачена вся площадь сечения балки (рис. 12.8, г). Это соответствует случаю, когда несущая способность балки будет исчерпана.
(рис. 12.8, в). Наконец, текучестью будет охвачена вся площадь сечения балки (рис. 12.8, г). Это соответствует случаю, когда несущая способность балки будет исчерпана.
Возникновение полной текучести в опасном поперечном сечении можно уподобить образованию в этом сечении так называемого пластического шарнира (рис. 12.9), который превращает балку в геометрически измененную систему и ее части раздельно поворачиваются в шарнире друг относительно друга. При этом поперечная нагрузка будет соответствовать своему предельному значению 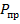 .
.
Величина изгибающего момента балки в месте шарнира называется предельным изгибающим моментом 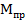 (см.рис.12.9), равным
(см.рис.12.9), равным
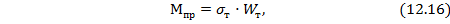
где 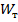 – предельный (пластический) момент сопротивления сечения балки.
– предельный (пластический) момент сопротивления сечения балки.
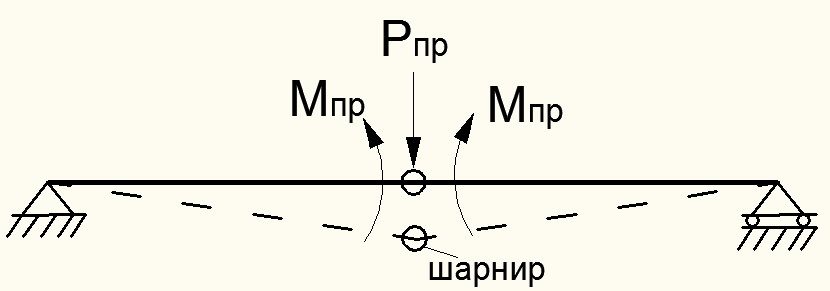
Рисунок 12.9 – Возникновение пластического шарнира балки в предельном состоянии
При симметричном относительно н.о. сечении балки (см. рис. 12.8) величина 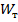 равна:
равна:
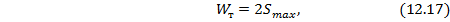
где 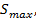 - статический момент половины сечения балки относительно н.о.
- статический момент половины сечения балки относительно н.о.
Например, для прямоугольного поперечного сечения балки (рис.12.10) предельный момент сопротивления будет:
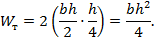
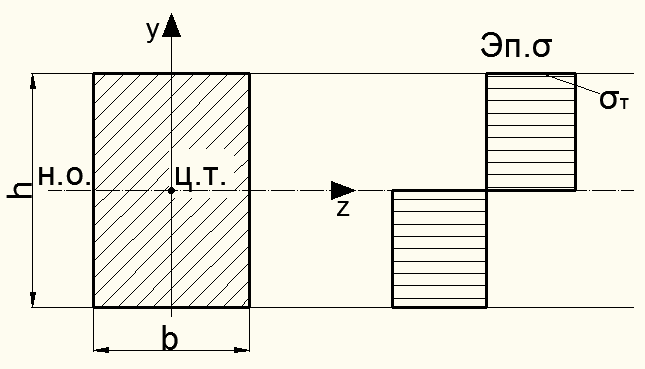
Рисунок 12.10 – К вычислению 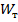 для прямоугольного сечения
для прямоугольного сечения
При несимметричном поперечном сечении балки относительно н.о. (рис. 12.11) охват текучестью всего сечения делит его на две равновеликие части 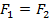 и предельный момент сопротивления определяется по формуле:
и предельный момент сопротивления определяется по формуле:
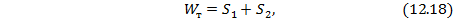
где 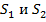 – статические моменты (
– статические моменты ( 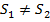 ) сечений балки
) сечений балки 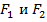 относительно н.о. (учитываются по абсолютной величине).
относительно н.о. (учитываются по абсолютной величине).
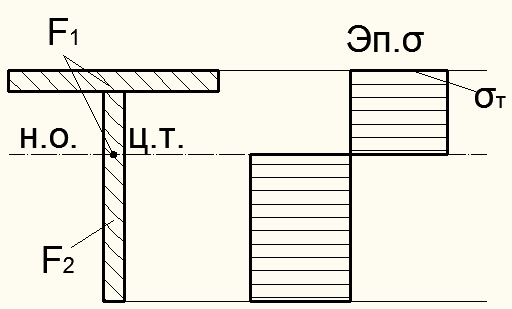
Рисунок 12.11 – К вычислению 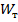 для несимметричного сечения
для несимметричного сечения
Предельный изгибающий момент для этого сечения рассчитывается по формуле (12.16).
Изгибающий момент для балки, при котором максимальные напряжения в наиболее удаленных от н.о. точках сечения равны пределу текучести материала, равен:
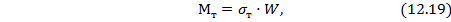
где 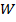 – момент сопротивления сечения балки относительно его крайней точки.
– момент сопротивления сечения балки относительно его крайней точки.
Этот момент считается опасным с позиции расчета балки по допускаемым напряжениям (опасной точки).
Из приведенных формул (12.16) и (12.19) имеет место соотношение 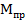 к
к 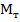 или
или 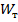 к
к 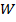 :
:
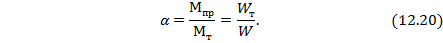
Величина этого отношения определяется формой поперечного сечения балки. Так, для балки прямоугольного поперечного сечения 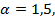 а для прокатного симметричного двутавра
а для прокатного симметричного двутавра 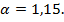
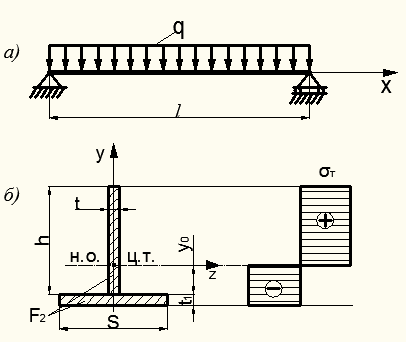 Пример 12.2. Определить допускаемую величину интенсивности распределенной нагрузки для двухопорной стальной балки (рис. 12.12, а), поперечное сечение которой изображено на рис. 12.12, б. Предел текучести материала
Пример 12.2. Определить допускаемую величину интенсивности распределенной нагрузки для двухопорной стальной балки (рис. 12.12, а), поперечное сечение которой изображено на рис. 12.12, б. Предел текучести материала 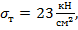 требуемый коэффициент запаса
требуемый коэффициент запаса 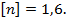
Рисунок 12.12 – К расчету несущей способности изгибаемой балки
Решение
1. Находим положение н.о. поперечного сечения балки из условия того, что в предельном состоянии н.о. делит сечение на две равновеликие части (см.рис.12.12):
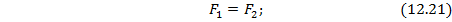
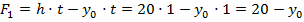
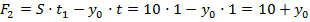
Подставляем полученные выражения в условие (12.21) и определяем положение н.о. сечения балки в предельном состоянии:
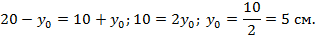
2. Рассчитываем статические моменты полусечений балки относительно н.о.:
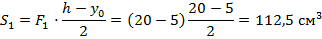
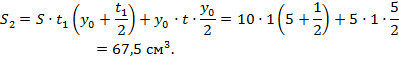
3. Предельный момент сопротивления сечения равен:
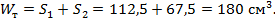
4. Предельный изгибающий момент для балки:
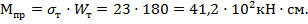
5. Рассчитываем допускаемый изгибающий момент балки в предельном состоянии:
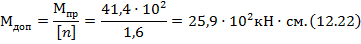
6. Наибольший изгибающий момент посредине пролета балки от заданной внешней нагрузки (см. рис.12.12,а) выражается формулой:
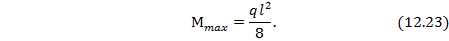
7. Считается, что внешняя нагрузка в формуле (12.23) равна допускаемой 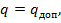 приравниваем значения
приравниваем значения 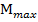 и
и 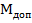
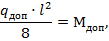
откуда
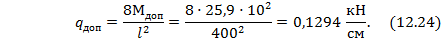
Дата добавления: 2016-10-18; просмотров: 3413;











