Пример решения типовой задачи о расчете геометрических характеристик сечения бруса. Задания для индивидуальной работы
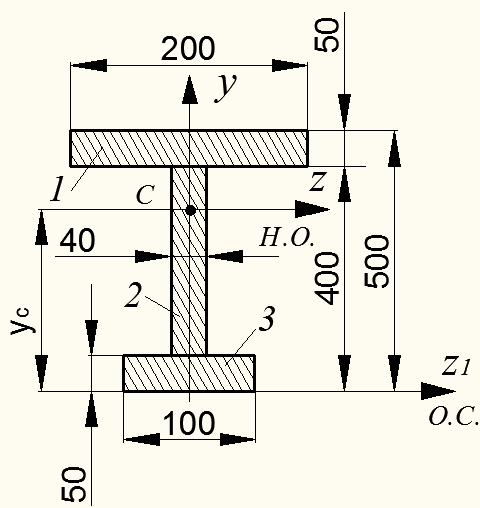 Пример 5.1. Для сечения составного двутавра (рис. 5.6) определить положение центра тяжести и центральный момент инерции Iz относительно горизонтальной оси z, проходящей через центр тяжести сечения (размеры даны в мм).
Пример 5.1. Для сечения составного двутавра (рис. 5.6) определить положение центра тяжести и центральный момент инерции Iz относительно горизонтальной оси z, проходящей через центр тяжести сечения (размеры даны в мм).
Рисунок 5.6 – Сечение составного двутавра
Решение
Рассматриваемое сечение является сложным, состоящим из нескольких простых (верхняя и нижняя полки, стенка – см. рис. 5.6). Для определения геометрических характеристик сложных сечений выбирают произвольную ось сравнения (о.с.), от которой отсчитывают отстояние центров тяжести простых сечений. В нашем примере принято: ось сравнения (о.с) 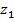 , нейтральная ось (н.о.) z, проходит через центр тяжести сечения т.С.
, нейтральная ось (н.о.) z, проходит через центр тяжести сечения т.С.
Требуемые в задании геометрические характеристики определим в следующей последовательности:
1.Сечение симметрично относительно вертикальной оси у, следовательно центр тяжести сечения (т.С) лежит на этой оси и 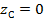 , а положение центра тяжести по вертикали ус рассчитываем по формуле:
, а положение центра тяжести по вертикали ус рассчитываем по формуле:
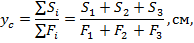
где 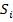 (і=1,2,3) – статические моменты элементов сечения, см3;
(і=1,2,3) – статические моменты элементов сечения, см3; 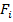 – площади сечений этих элементов, см2.
– площади сечений этих элементов, см2.
Для верхней полки 1 – см. рис. 5.6: 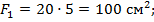 центр тяжести этой полки отстоит от о.с. на расстоянии
центр тяжести этой полки отстоит от о.с. на расстоянии 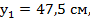 поэтому
поэтому 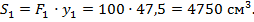
Для стенки 2: 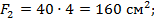 центр тяжести стенки отстоит от о.с. на расстояние
центр тяжести стенки отстоит от о.с. на расстояние 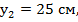 поэтому
поэтому 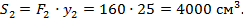
Для нижней полки 3: 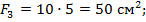 центр тяжести этой полки отстоит от о.с. на расстоянии
центр тяжести этой полки отстоит от о.с. на расстоянии 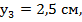 поэтому
поэтому 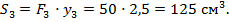
Тогда ордината центра тяжести всего сечения равна:
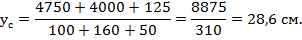
2. Центральный момент инерции всего сечения относительно нейтральной оси z, проходящий через центр тяжести сечения (т.С), рассчитывается по формуле:
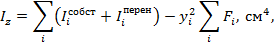
где 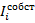 – собственные моменты инерции составляющих сечение элементов относительно горизонтальных осей, которые проходят через их центры тяжести,
– собственные моменты инерции составляющих сечение элементов относительно горизонтальных осей, которые проходят через их центры тяжести, 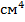 ;
;  – переносные моменты инерции составляющих сечение элементов относительно о.с.
– переносные моменты инерции составляющих сечение элементов относительно о.с. 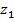 , см4.
, см4.
Элементы всего сечения представляют собой прямоугольники, моменты инерции которых относительно горизонтальной оси рассчитываются по формуле (см. табл. 5.1):
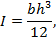
где 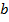 – ширина элемента сечения (горизонтальный размер);
– ширина элемента сечения (горизонтальный размер); 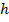 - высота элемента сечения.
- высота элемента сечения.
В нашем примере:
- для верхней полки 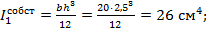
- для стенки 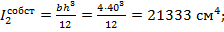
- для нижней полки 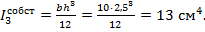
Выполним расчет переносных моментов инерции элементов сечения:
- для верхней полки
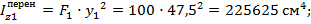
- для стенки
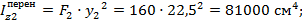
- для нижней стенки
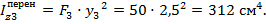
Тогда окончательно для всего сечения составного двутавра центральный момент инерции относительно центральной оси z будет равен:
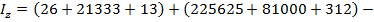
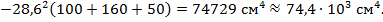
Дата добавления: 2016-10-18; просмотров: 8464;











