Решение типовой задачи о расчете кручения вала. Задания для индивидуальной работы

Пример 6.1.Вал постоянного круглого сечения (рис. 6.5) нагружен внешними скручивающими моментами 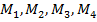. Значение трех моментов приведено на рисунке. Требуется: определить величину скручивающего момента 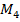; рассчитать величины крутящих моментов по участкам вала и построить эпюру 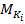; определить требуемый диаметр постоянного сечения вала, если допускаемое напряжение при кручении 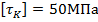; рассчитать углы закручивания вала 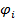относительно крайнего левого сечения и построить эпюру φ; определить наибольший относительный угол закручивания и сравнить его с допускаемой величиной .

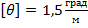Решение

1.Определить величину внешнего скручивающего момента 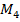из условий статики:

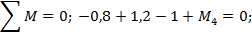
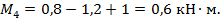
При составлении условий статики пользуемся, например, следующим правилом знаков для внешних моментов: при их направлении по часовой стрелке они принимаются со знаком плюс, против часовой стрелки – со знаком минус.

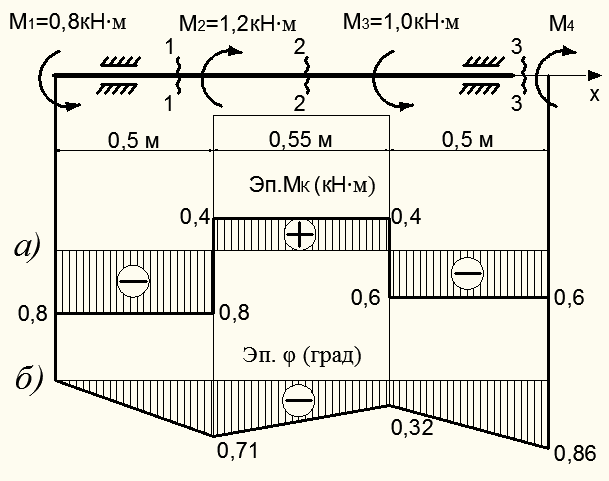
Рисунок 6.5 – Расчетная схема вала при скручивании

2. Разбиваем вал на участки: принимаются три участка 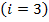между внешними скручивающими моментами. По участкам в отмеченных сечениях 1, 2, 3 (см. рис. 6.5) рассчитываем крутящие моменты :

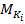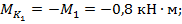
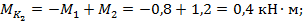
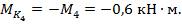
На основании выполненных расчетов строим эпюру 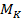(см. рис. 6.5, а). По эпюре определим наибольшее значение крутящего момента .

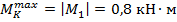3. Из условия прочности вала на кручение рассчитываем требуемый диаметр поперечного сечения вала:

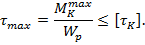
Так как для вала сплошного круглого сечения 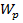= 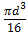, то

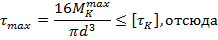
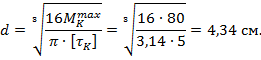
Округляя диаметр вала в большую сторону, принимаем .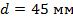

4. Определим жесткость вала на кручение :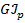

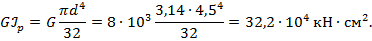
5. Рассчитаем углы закручивания границ участков относительно левого крайнего сечения:

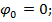
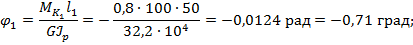
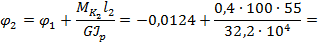
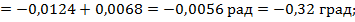
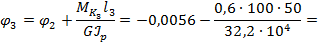
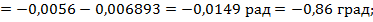
На основании выполненных расчетов строим эпюру углов закручивания вал φ (см. рис. 6.5, б).

6. Определить наибольший относительный угол закручивания 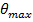. Он соответствует в нашем примере наибольшему по модулю крутящему моменту .

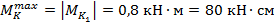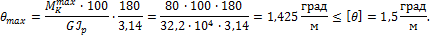
Следовательно, условие жесткости для вала выполняется.